1 . 变分法是研究变元函数达到极值的必要条件和充要条件,欧拉、拉格朗日等数学家为其奠定了理论基础,其中“平缓函数”是变分法中的一个重要概念.设 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 均成立,则称
均成立,则称 是“平缓函数”.
是“平缓函数”.
(1)若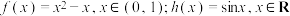 .试判断
.试判断 和
和 是否为“平缓函数”?并说明理由;(参考公式:①
是否为“平缓函数”?并说明理由;(参考公式:① 时,
时,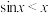 恒成立;②
恒成立;②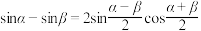 .)
.)
(2)若函数 是周期为2的“平缓函数”,证明:对定义域内任意的
是周期为2的“平缓函数”,证明:对定义域内任意的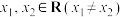 ,均有
,均有 ;
;
(3)设 为定义在
为定义在 上的函数,且存在正常数
上的函数,且存在正常数 ,使得函数
,使得函数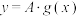 为“平缓函数”.现定义数列
为“平缓函数”.现定义数列 满足:
满足: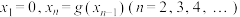 ,试证明:对任意的正整数
,试证明:对任意的正整数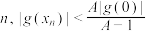 .
.
(参考公式: 且
且 时,
时,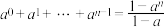 .)
.)
 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 均成立,则称
均成立,则称 是“平缓函数”.
是“平缓函数”.(1)若
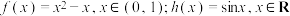 .试判断
.试判断 和
和 是否为“平缓函数”?并说明理由;(参考公式:①
是否为“平缓函数”?并说明理由;(参考公式:① 时,
时,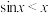 恒成立;②
恒成立;②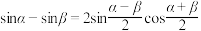 .)
.)(2)若函数
 是周期为2的“平缓函数”,证明:对定义域内任意的
是周期为2的“平缓函数”,证明:对定义域内任意的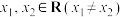 ,均有
,均有 ;
;(3)设
 为定义在
为定义在 上的函数,且存在正常数
上的函数,且存在正常数 ,使得函数
,使得函数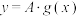 为“平缓函数”.现定义数列
为“平缓函数”.现定义数列 满足:
满足: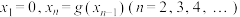 ,试证明:对任意的正整数
,试证明:对任意的正整数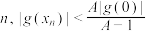 .
.(参考公式:
 且
且 时,
时,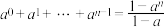 .)
.)
您最近一年使用:0次
2024-04-26更新
|
388次组卷
|
3卷引用:云南省昆明市云南师范大学附属中学2023-2024学年高一下学期教学测评期中卷数学试卷
云南省昆明市云南师范大学附属中学2023-2024学年高一下学期教学测评期中卷数学试卷四川省成都市成飞中学2023-2024学年高一下学期5月月考数学试题(已下线)专题10 利用微分中值法证明不等式【讲】
2 . 对于定义域为R的函数 ,若存在常数
,若存在常数 ,使得
,使得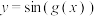 是以
是以 为周期的周期函数,则称
为周期的周期函数,则称 为“正弦周期函数”,且称
为“正弦周期函数”,且称 为其“正弦周期”.
为其“正弦周期”.
(1)判断函数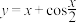 是否为“正弦周期函数”,并说明理由;
是否为“正弦周期函数”,并说明理由;
(2)已知 是定义在R上的严格增函数,值域为R,且
是定义在R上的严格增函数,值域为R,且 是以
是以 为“正弦周期”的“正弦周期函数”,若
为“正弦周期”的“正弦周期函数”,若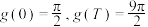 ,且存在
,且存在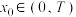 ,使得
,使得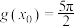 ,求
,求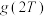 的值;
的值;
(3)已知 是以
是以 为一个“正弦周期”的“正弦周期函数”,且存在
为一个“正弦周期”的“正弦周期函数”,且存在 和
和 ,使得对任意
,使得对任意 ,都有
,都有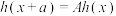 ,证明:
,证明: 是周期函数.
是周期函数.
 ,若存在常数
,若存在常数 ,使得
,使得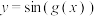 是以
是以 为周期的周期函数,则称
为周期的周期函数,则称 为“正弦周期函数”,且称
为“正弦周期函数”,且称 为其“正弦周期”.
为其“正弦周期”.(1)判断函数
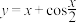 是否为“正弦周期函数”,并说明理由;
是否为“正弦周期函数”,并说明理由;(2)已知
 是定义在R上的严格增函数,值域为R,且
是定义在R上的严格增函数,值域为R,且 是以
是以 为“正弦周期”的“正弦周期函数”,若
为“正弦周期”的“正弦周期函数”,若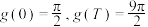 ,且存在
,且存在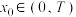 ,使得
,使得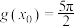 ,求
,求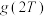 的值;
的值;(3)已知
 是以
是以 为一个“正弦周期”的“正弦周期函数”,且存在
为一个“正弦周期”的“正弦周期函数”,且存在 和
和 ,使得对任意
,使得对任意 ,都有
,都有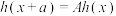 ,证明:
,证明: 是周期函数.
是周期函数.
您最近一年使用:0次
解题方法
3 . 若函数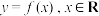 的导函数
的导函数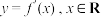 是以
是以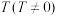 为周期的函数,则称函数
为周期的函数,则称函数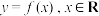 具有“
具有“ 性质”.
性质”.
(1)试判断函数
 和
和 是否具有“
是否具有“ 性质”,并说明理由;
性质”,并说明理由;(2)已知函数
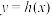 ,其中
,其中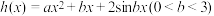 具有“
具有“ 性质”,求函数
性质”,求函数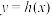 在
在 上的极小值点;
上的极小值点;(3)若函数
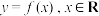 具有“
具有“ 性质”,且存在实数
性质”,且存在实数 使得对任意
使得对任意 都有
都有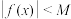 成立,求证:
成立,求证: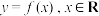 为周期函数.
为周期函数.(可用结论:若函数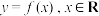 的导函数满足
的导函数满足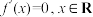 ,则
,则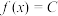 (常数).)
(常数).)
您最近一年使用:0次
名校
解题方法
4 . 若存在常数 、
、 ,使得函数
,使得函数 对于
对于 同时满足:
同时满足: ,
, ,则称函数
,则称函数 为“
为“ ”类函数.
”类函数.
(1)判断函数 是否为“
是否为“ ”类函数?如果是,写出一组
”类函数?如果是,写出一组 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;
(2)函数 是“
是“ ”类函数,且当
”类函数,且当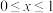 时,
时,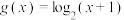 .
.
①证明: 是周期函数,并求出
是周期函数,并求出 在
在 上的解析式;
上的解析式;
②若 ,
,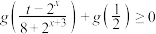 ,求
,求 的最大值和最小值.
的最大值和最小值.
 、
、 ,使得函数
,使得函数 对于
对于 同时满足:
同时满足: ,
, ,则称函数
,则称函数 为“
为“ ”类函数.
”类函数.(1)判断函数
 是否为“
是否为“ ”类函数?如果是,写出一组
”类函数?如果是,写出一组 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;(2)函数
 是“
是“ ”类函数,且当
”类函数,且当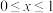 时,
时,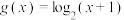 .
.①证明:
 是周期函数,并求出
是周期函数,并求出 在
在 上的解析式;
上的解析式;②若
 ,
,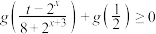 ,求
,求 的最大值和最小值.
的最大值和最小值.
您最近一年使用:0次
2024-03-15更新
|
282次组卷
|
2卷引用:湖南省长沙市长郡中学2023-2024学年高一下学期寒假检测(开学考试)数学试题
名校
解题方法
5 . 已知函数 的定义域为
的定义域为 且满足:对任意的
且满足:对任意的 ,有
,有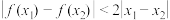 恒成立,则称
恒成立,则称 为“
为“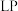 ”函数.
”函数.
(1)分别判断 和
和 是否为“
是否为“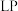 ”函数.(直接写出结果)
”函数.(直接写出结果)
(2)若 为
为 上的“
上的“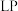 ”函数,且
”函数,且 是以4为周期的周期函数,证明;对任意的
是以4为周期的周期函数,证明;对任意的 ,
,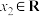 ,都有:
,都有: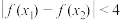 .
.
 的定义域为
的定义域为 且满足:对任意的
且满足:对任意的 ,有
,有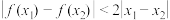 恒成立,则称
恒成立,则称 为“
为“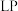 ”函数.
”函数.(1)分别判断
 和
和 是否为“
是否为“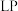 ”函数.(直接写出结果)
”函数.(直接写出结果)(2)若
 为
为 上的“
上的“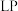 ”函数,且
”函数,且 是以4为周期的周期函数,证明;对任意的
是以4为周期的周期函数,证明;对任意的 ,
,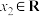 ,都有:
,都有: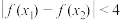 .
.
您最近一年使用:0次
名校
解题方法
6 . 已知函数 的定义域为
的定义域为 ,
,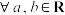 ,
, ,且
,且 在区间
在区间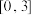 上单调递减.
上单调递减.
(1)求证: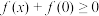 ;
;
(2)求 的值;
的值;
(3)当 时,求不等式
时,求不等式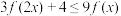 的解集.
的解集.
 的定义域为
的定义域为 ,
,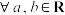 ,
, ,且
,且 在区间
在区间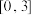 上单调递减.
上单调递减.(1)求证:
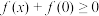 ;
;(2)求
 的值;
的值;(3)当
 时,求不等式
时,求不等式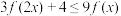 的解集.
的解集.
您最近一年使用:0次
2024-01-24更新
|
361次组卷
|
2卷引用:广东省广州市越秀区2023-2024学年高一上学期期末数学试题
7 . 设 ,对定义在
,对定义在 上的函数
上的函数 ,若存在常数
,若存在常数 ,使得
,使得 对任意
对任意 恒成立,则称函数
恒成立,则称函数 满足性质
满足性质 .
.
(1)判断下列函数是否具有性质 ?
?
①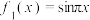 ,②
,② ,③
,③ .
.
(2)若函数 具有性质
具有性质 ,其中
,其中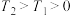 ,求证:函数
,求证:函数 具有性质
具有性质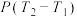 ;
;
(3)设函数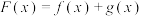 具有性质
具有性质 ,其中
,其中 是奇函数,
是奇函数, 是偶函数.若
是偶函数.若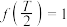 ,求
,求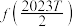 的值.
的值.
 ,对定义在
,对定义在 上的函数
上的函数 ,若存在常数
,若存在常数 ,使得
,使得 对任意
对任意 恒成立,则称函数
恒成立,则称函数 满足性质
满足性质 .
.(1)判断下列函数是否具有性质
 ?
?①
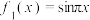 ,②
,② ,③
,③ .
.(2)若函数
 具有性质
具有性质 ,其中
,其中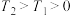 ,求证:函数
,求证:函数 具有性质
具有性质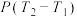 ;
;(3)设函数
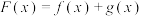 具有性质
具有性质 ,其中
,其中 是奇函数,
是奇函数, 是偶函数.若
是偶函数.若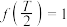 ,求
,求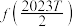 的值.
的值.
您最近一年使用:0次
8 . 设 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 、
、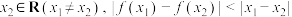 均成立, 则称
均成立, 则称 是“平缓函数”.
是“平缓函数”.
(1)若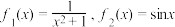 , 试判断
, 试判断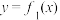 和
和 是否为“平缓函数” ? 并说明理由; (参考公式:
是否为“平缓函数” ? 并说明理由; (参考公式: 时,
时,  恒成立)
恒成立)
(2)若函数 是“平缓函数”, 且
是“平缓函数”, 且 是以 1为周期的周期函数, 证明:对任意的
是以 1为周期的周期函数, 证明:对任意的 、
、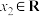 , 均有
, 均有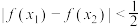 ;
;
(3)设 为定义在
为定义在 上函数, 且存在正常数
上函数, 且存在正常数 使得函数
使得函数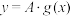 为“平缓函数”. 现定义数列
为“平缓函数”. 现定义数列 满足:
满足: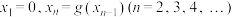 , 试证明:对任意的正整数
, 试证明:对任意的正整数 .
.
 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 、
、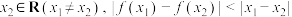 均成立, 则称
均成立, 则称 是“平缓函数”.
是“平缓函数”.(1)若
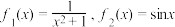 , 试判断
, 试判断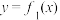 和
和 是否为“平缓函数” ? 并说明理由; (参考公式:
是否为“平缓函数” ? 并说明理由; (参考公式: 时,
时,  恒成立)
恒成立)(2)若函数
 是“平缓函数”, 且
是“平缓函数”, 且 是以 1为周期的周期函数, 证明:对任意的
是以 1为周期的周期函数, 证明:对任意的 、
、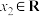 , 均有
, 均有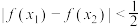 ;
;(3)设
 为定义在
为定义在 上函数, 且存在正常数
上函数, 且存在正常数 使得函数
使得函数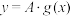 为“平缓函数”. 现定义数列
为“平缓函数”. 现定义数列 满足:
满足: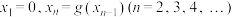 , 试证明:对任意的正整数
, 试证明:对任意的正整数 .
.
您最近一年使用:0次
名校
9 . 已知函数 ,
, ,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有
,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有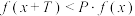 成立,则称函数
成立,则称函数 是D上的P级递减周期函数,周期为T;若恒有
是D上的P级递减周期函数,周期为T;若恒有 成立,则称函数
成立,则称函数 是D上的P级周期函数,周期为T.
是D上的P级周期函数,周期为T.
(1)判断函数 是R上的周期为1的2级递减周期函数吗,并说明理由?
是R上的周期为1的2级递减周期函数吗,并说明理由?
(2)已知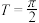 ,
, 是
是 上的P级周期函数,且
上的P级周期函数,且 是
是 上的严格增函数,当
上的严格增函数,当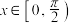 时,
时,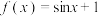 .求当
.求当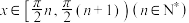 时,函数
时,函数 的解析式,并求实数P的取值范围;
的解析式,并求实数P的取值范围;
(3)是否存在非零实数k,使函数 是R上的周期为T的T级周期函数?请证明你的结论.
是R上的周期为T的T级周期函数?请证明你的结论.
 ,
, ,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有
,如果对于定义域D内的任意实数x,对于给定的非零常数P,总存在非零常数T,恒有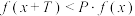 成立,则称函数
成立,则称函数 是D上的P级递减周期函数,周期为T;若恒有
是D上的P级递减周期函数,周期为T;若恒有 成立,则称函数
成立,则称函数 是D上的P级周期函数,周期为T.
是D上的P级周期函数,周期为T.(1)判断函数
 是R上的周期为1的2级递减周期函数吗,并说明理由?
是R上的周期为1的2级递减周期函数吗,并说明理由?(2)已知
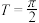 ,
, 是
是 上的P级周期函数,且
上的P级周期函数,且 是
是 上的严格增函数,当
上的严格增函数,当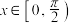 时,
时,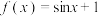 .求当
.求当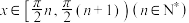 时,函数
时,函数 的解析式,并求实数P的取值范围;
的解析式,并求实数P的取值范围;(3)是否存在非零实数k,使函数
 是R上的周期为T的T级周期函数?请证明你的结论.
是R上的周期为T的T级周期函数?请证明你的结论.
您最近一年使用:0次
2022-04-26更新
|
2111次组卷
|
10卷引用:上海市闵行区(闵行中学、文绮中学)2021-2022学年高一下学期期中数学试题
上海市闵行区(闵行中学、文绮中学)2021-2022学年高一下学期期中数学试题广东省广州市三校联考2021-2022学年高一下学期期中数学试题上海市复旦大学附属中学青浦分校2022-2023学年高一下学期3月月考数学试题上海市文来中学2022-2023学年高一下学期期中数学试题广东省惠州市2022-2023学年高一下学期期末数学试题福建省德化第二中学2022-2023学年高一下学期期中考试数学试题福建省福州市四校教学联盟2023-2024学年高一上学期1月期末学业联考数学试题(已下线)专题11 期末预测能力卷-期末复习重难培优与单元检测(人教A版2019)江西省南昌市江西师大附中2023-2024学年高一下学期3月素养测试数学试题江西省宜春市丰城中学2023-2024学年高一下学期4月期中考试数学试题
解题方法
10 . 函数 ,其中
,其中 是定义在
是定义在 上的周期函数,
上的周期函数,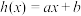 ,
, 为常数
为常数
(1)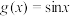 ,讨论
,讨论 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求证:“ 为奇函数“的一个必要非充分条件是”
为奇函数“的一个必要非充分条件是” 的图象有异于原点的对称中心
的图象有异于原点的对称中心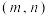 ”
”
(3) ,
, 在
在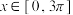 上的最大值为
上的最大值为 ,求
,求 的最小值.
的最小值.
 ,其中
,其中 是定义在
是定义在 上的周期函数,
上的周期函数,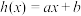 ,
, 为常数
为常数(1)
 ,讨论
,讨论 的奇偶性,并说明理由;
的奇偶性,并说明理由;(2)求证:“
 为奇函数“的一个必要非充分条件是”
为奇函数“的一个必要非充分条件是” 的图象有异于原点的对称中心
的图象有异于原点的对称中心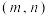 ”
”(3)
 ,
, 在
在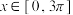 上的最大值为
上的最大值为 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次



