1 . 某啤酒厂为适应市场需要,2011年起引进葡萄酒生产线,同时生产啤酒和葡萄酒,2011年啤酒生产量为16000吨,葡萄酒生产量1000吨.该厂计划从2012年起每年啤酒的生产量是上一年的一半,葡萄酒生产量是上一年的两倍,试问:
(1)哪一年啤酒与葡萄酒的年生产量之和最低?
(2)从2011年起(包括2011年),经过多少年葡萄酒的生产总量不低于该厂啤酒与葡萄酒生产总量之和的 ?(生产总量是指各年年产量之和)
?(生产总量是指各年年产量之和)
(1)哪一年啤酒与葡萄酒的年生产量之和最低?
(2)从2011年起(包括2011年),经过多少年葡萄酒的生产总量不低于该厂啤酒与葡萄酒生产总量之和的
 ?(生产总量是指各年年产量之和)
?(生产总量是指各年年产量之和)
您最近一年使用:0次
2021-03-31更新
|
171次组卷
|
3卷引用:河南省濮阳市第一高级中学2021-2022学年高二上学期期中质量检测数学(理)试题
20-21高三下·河南·阶段练习
解题方法
2 . 已知数列 是公差为
是公差为 的等差数列,设
的等差数列,设 ,若存在常数
,若存在常数 ,使得数列
,使得数列 为等比数列,则
为等比数列,则 的值为
的值为___________ .
 是公差为
是公差为 的等差数列,设
的等差数列,设 ,若存在常数
,若存在常数 ,使得数列
,使得数列 为等比数列,则
为等比数列,则 的值为
的值为
您最近一年使用:0次
2021-02-23更新
|
855次组卷
|
7卷引用:河南省九师联盟2020-2021年高三下学期2月联考理科数学试题
(已下线)河南省九师联盟2020-2021年高三下学期2月联考理科数学试题(已下线)押第15题 数列-备战2021年高考数学(理)临考题号押题(全国卷1)(已下线)专题10 数列(难点)-2020-2021学年高二数学下学期期末专项复习(北师大版2019选择性必修第一册、第二册)(已下线)专题09 《数列》中的存在性问题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)(已下线)第四章 数列(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第一册)(已下线)专题09 数列的通项公式、数列求和及综合应用(练习)-1(已下线)压轴小题6 等差数列求参数
21-22高三上·河南三门峡·期末
解题方法
3 . 已知各项为正数的等比数列 ,前
,前 项和为
项和为 ,若
,若 成等差数列,
成等差数列,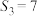 ,数列
,数列 满足,
满足, ,数列
,数列 的前
的前 项和为
项和为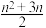
(1)求 的公比
的公比 的值;
的值;
(2)求 的通项公式.
的通项公式.
 ,前
,前 项和为
项和为 ,若
,若 成等差数列,
成等差数列,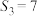 ,数列
,数列 满足,
满足, ,数列
,数列 的前
的前 项和为
项和为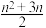
(1)求
 的公比
的公比 的值;
的值;(2)求
 的通项公式.
的通项公式.
您最近一年使用:0次
10-11高三·浙江·阶段练习
名校
解题方法
4 . 已知数列 的首项
的首项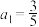 ,且满足
,且满足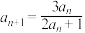 .
.
(1)求证:数列 为等比数列.
为等比数列.
(2)若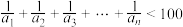 ,求满足条件的最大整数n.
,求满足条件的最大整数n.
 的首项
的首项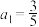 ,且满足
,且满足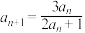 .
.(1)求证:数列
 为等比数列.
为等比数列.(2)若
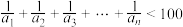 ,求满足条件的最大整数n.
,求满足条件的最大整数n.
您最近一年使用:0次
2021-02-07更新
|
3910次组卷
|
27卷引用:河南省南阳市第一中学校2021-2022学年高二上学期第一次月考数学试题
河南省南阳市第一中学校2021-2022学年高二上学期第一次月考数学试题人教A版(2019) 选择性必修第二册 新高考名师导学 第四章 4.3 等比数列江苏省徐州市2020-2021学年高二下学期期末数学试题(已下线)4.3 等比数列福建省三明第一中学2022届高三上学期学段考数学试题湖南省长沙市雅礼中学2021-2022学年高三上学期月考(五)数学试题河南省许昌市建安区第一高级中学2023-2024学年高二上学期12月月考数学试题(已下线)2011届浙江省六校高三2月月考数学理卷(已下线)2018年9月22日 《每日一题》人教必修5-周末培优上海市2018-2019学年高一第二学期期末复习卷数学试题上海市金山中学2018-2019学年高一下学期期末考试数学试题上海市七宝中学2017-2018学年高一下学期期末数学试题(已下线)专题36 不等式综合练习-2021年高考一轮数学(理)单元复习一遍过(已下线)专题36 不等式综合练习-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题36 不等式综合练习-2021年高考一轮数学(文)单元复习一遍过江苏省镇江市扬中市第二高级中学2021-2022学年高二下学期3月阶段测试数学试题黑龙江省牡丹江市海林市朝鲜族中学2022-2023学年高三上学期第二次月考数学(理)试题江苏省镇江市句容碧桂园学校2022-2023学年高二上学期第二次月考模拟数学试题湖南省长沙市弘益高级中学2022-2023学年高三上学期第四次月考数学试题江苏省南京市第十三中学2022-2023学年高三上学期期末数学试题黑龙江省哈尔滨师范大学附属中学2023届高三第四次模拟考试数学试题(已下线)专题07 数列-2人教A版(2019)选择性必修第二册课本习题 习题4.3湖南省岳阳市平江县2023-2024学年高二上学期期末教学质量监测数学试题四川省南充市白塔中学2023-2024学年高二下学期期中考试数学试题(已下线)第03讲 等比数列及其前n项和(九大题型)(讲义)-2(已下线)第05讲 数列求和(十三大题型)(讲义)-2
5 . 已知 是公差为3的等差数列,数列
是公差为3的等差数列,数列 满足
满足 ,
, ,
,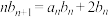 .
.
(1)求 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
 是公差为3的等差数列,数列
是公差为3的等差数列,数列 满足
满足 ,
, ,
,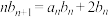 .
.(1)求
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 .
.
您最近一年使用:0次
解题方法
6 . 已知等比数列 的前
的前 项和为
项和为 ,公比
,公比 ,
, ,
,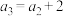 .若数列
.若数列 的前
的前 项和为
项和为 ,
, ,则
,则 ( )
( )
 的前
的前 项和为
项和为 ,公比
,公比 ,
, ,
,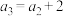 .若数列
.若数列 的前
的前 项和为
项和为 ,
, ,则
,则 ( )
( )A.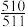 | B.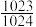 | C.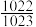 | D.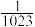 |
您最近一年使用:0次
2021-02-04更新
|
367次组卷
|
5卷引用:河南省天一大联考2020-2021学年高二上学期期末考试文科数学试题
河南省天一大联考2020-2021学年高二上学期期末考试文科数学试题安徽省亳州市2020-2021学年高二上学期期末文科数学试题(已下线)期末测试卷02-2020-2021学年高二数学下学期期末专项复习(北师大版2019选择性必修第一册、第二册)人教B版(2019) 选修第三册 必杀技 第五章 5.3.2 课时2 等比数列的前n项和(2)2023版 湘教版(2019) 选修第一册 过关斩将 第1章 1.3.3 等比数列的前n项的和
7 . 设 是等差数列
是等差数列 的前
的前 项和,已知
项和,已知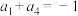 ,
, .
.
(1)求 ;
;
(2)若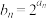 ,求数列
,求数列 的前
的前 项和
项和 .
.
 是等差数列
是等差数列 的前
的前 项和,已知
项和,已知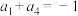 ,
, .
.(1)求
 ;
;(2)若
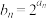 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
8 . 已知等比数列 的前
的前 项和为
项和为 ,公比
,公比 ,
, ,
,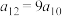 ,要使数列
,要使数列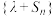 为等比数列,则实数
为等比数列,则实数 的值为( )
的值为( )
 的前
的前 项和为
项和为 ,公比
,公比 ,
, ,
,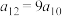 ,要使数列
,要使数列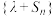 为等比数列,则实数
为等比数列,则实数 的值为( )
的值为( )A. | B. | C.2 | D.不存在 |
您最近一年使用:0次
2021-02-02更新
|
482次组卷
|
5卷引用:河南省鹤壁市2020-2021学年高二上学期期末数学理科试题
9 . 设 是等差数列
是等差数列 的前
的前 项和,已知
项和,已知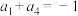 ,
, .
.
(1)求 ;
;
(2)若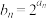 ,求数列
,求数列 的前
的前 项和
项和 .
.
 是等差数列
是等差数列 的前
的前 项和,已知
项和,已知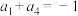 ,
, .
.(1)求
 ;
;(2)若
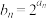 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
21-22高三上·辽宁·期末
解题方法
10 . 设数列 的前
的前 项和为
项和为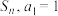 ,且
,且 成等差数列.
成等差数列.
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为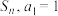 ,且
,且 成等差数列.
成等差数列.(1)证明:数列
 是等比数列;
是等比数列;(2)求数列
 的前
的前 项和
项和 .
.
您最近一年使用:0次
2021-01-23更新
|
358次组卷
|
7卷引用:河南省新乡市诚城卓人学校2021-2022学年高二上学期12月月考数学文科试题



