1 . 在正方体 中,点
中,点 满足
满足 ,其中
,其中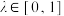 ,
, ,则( )
,则( )
 中,点
中,点 满足
满足 ,其中
,其中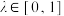 ,
, ,则( )
,则( )A.当 时, 时,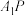  平面 平面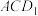 |
B.当 时,三棱锥 时,三棱锥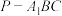 的体积为定值 的体积为定值 |
C.当 时, 时, 的面积为定值 的面积为定值 |
D.当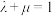 时,直线 时,直线 与 与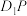 所成角的范围为 所成角的范围为 |
您最近一年使用:0次
7日内更新
|
184次组卷
|
14卷引用:湖北省五校(郧阳中学、恩施高中、沙市中学、随州二中、襄阳三中)2022-2023学年高二上学期11月期中联考数学试题
湖北省五校(郧阳中学、恩施高中、沙市中学、随州二中、襄阳三中)2022-2023学年高二上学期11月期中联考数学试题浙江省绍兴市2021-2022学年高二下学期期末数学试题(已下线)突破1.4 空间向量的应用(课时训练)江西省上饶市广丰区重点高中2022-2023学年高二上学期期中考试数学试题浙江省金华第一中学2023-2024学年高二上学期11月期中数学试题四川省泸州市泸县泸县第五中学2023-2024学年高二上学期期中数学试题浙江省湖州市安吉振民高级中学2023-2024学年高二上学期期中数学试题重庆市黔江中学校2023-2024学年高二上学期10月考试数学试题浙江省金华市武义第一中学2023-2024学年高二上学期12月检测1数学试题浙江省温州市第二十二中学2022-2023学年高二暑假返校检测数学试题广东省茂名市化州市第一中学2024-2025学年高二上学期10月月考数学试题湖南省永州市第一中学2022-2023学年高三上学期第三次月考数学试题重庆市2023届高三下学期第一次联考数学试题(已下线)重难点突破05 立体几何中的常考压轴小题(七大题型)-1
名校
2 . 如图,正方体 的棱长为1,点
的棱长为1,点 在线段
在线段 上运动,则下列选项中正确的是( )
上运动,则下列选项中正确的是( )
 的棱长为1,点
的棱长为1,点 在线段
在线段 上运动,则下列选项中正确的是( )
上运动,则下列选项中正确的是( )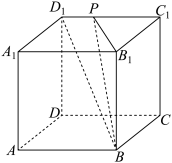
A. 的最小值为 的最小值为 . . |
B.平面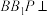 平面 平面 . . |
C.若 是 是 的中点,则二面角 的中点,则二面角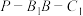 的余弦值为 的余弦值为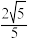 . . |
D.若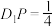 ,则直线 ,则直线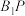 与 与 所成角的余弦值为 所成角的余弦值为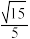 . . |
您最近一年使用:0次
解题方法
3 . 如图,在正三棱柱 中,
中, 分别为棱
分别为棱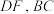 的中点,
的中点, ,则异面直线
,则异面直线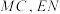 所成角的余弦值为( )
所成角的余弦值为( )
 中,
中, 分别为棱
分别为棱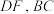 的中点,
的中点, ,则异面直线
,则异面直线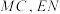 所成角的余弦值为( )
所成角的余弦值为( )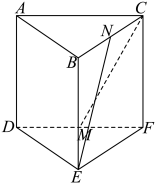
A.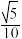 | B. | C.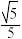 | D.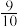 |
您最近一年使用:0次
2024-09-04更新
|
198次组卷
|
2卷引用:湖北省十堰市竹溪县第二高级中学2024-2025学年高二上学期9月月考数学试卷
名校
解题方法
4 . 如图,在正方体 中,
中, 分别为
分别为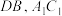 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )
 中,
中, 分别为
分别为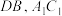 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )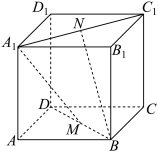
A.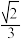 | B. | C. | D. |
您最近一年使用:0次
2024-09-03更新
|
1261次组卷
|
5卷引用:湖北省宜昌市长阳土家族自治县第二高级中学2024-2025学年高二上学期9月考试数学试题
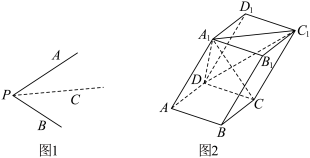
5 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理,如图1,由射线PA,PB,PC构成的三面角P-ABC,记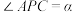 ,
,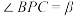 ,
, ,二面角A-PC-B的大小为
,二面角A-PC-B的大小为 ,则
,则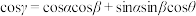 .
.
如图2,四棱柱 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,
,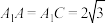 ,
, ,且
,且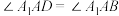 .
.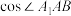 的值;
的值;
(2)在图2中,直线 与平面ABCD内任意一条直线的夹角为φ,证明:
与平面ABCD内任意一条直线的夹角为φ,证明: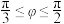 ;
;
(3)在图2中,过点B作平面 ,使平面
,使平面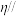 平面
平面 ,且与直线
,且与直线 相交于点P,求
相交于点P,求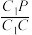 的值.
的值.
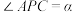 ,
,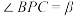 ,
, ,二面角A-PC-B的大小为
,二面角A-PC-B的大小为 ,则
,则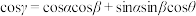 .
.如图2,四棱柱
 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,
,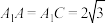 ,
, ,且
,且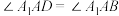 .
.
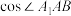 的值;
的值;(2)在图2中,直线
 与平面ABCD内任意一条直线的夹角为φ,证明:
与平面ABCD内任意一条直线的夹角为φ,证明: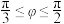 ;
;(3)在图2中,过点B作平面
 ,使平面
,使平面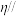 平面
平面 ,且与直线
,且与直线 相交于点P,求
相交于点P,求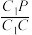 的值.
的值.
您最近一年使用:0次
2024-09-03更新
|
317次组卷
|
2卷引用:湖北省鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高二上学期起点考试数学试卷
名校
6 . 如图为一正方体的平面展开图,在这个正方体中,有下列四个命题: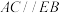 ;
;
② 与
与 成60°角;
成60°角;
③ 与
与 成异面直线且
成异面直线且 ;
;
④若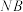 与平面
与平面 所成角为
所成角为 ,则
,则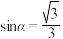 .
.
其中正确的序号是__________ .
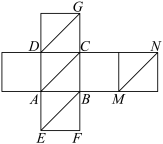
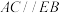 ;
;②
 与
与 成60°角;
成60°角;③
 与
与 成异面直线且
成异面直线且 ;
;④若
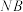 与平面
与平面 所成角为
所成角为 ,则
,则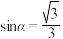 .
.其中正确的序号是
您最近一年使用:0次
7 . 如图,在平行六面体 中,底面
中,底面 是菱形,侧面
是菱形,侧面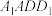 是正方形,且
是正方形,且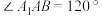 ,
,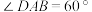 ,
, ,若P是
,若P是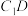 与
与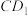 的交点,则异面直线
的交点,则异面直线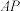 与
与 的夹角的余弦值为( )
的夹角的余弦值为( )
 中,底面
中,底面 是菱形,侧面
是菱形,侧面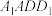 是正方形,且
是正方形,且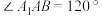 ,
,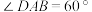 ,
, ,若P是
,若P是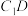 与
与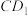 的交点,则异面直线
的交点,则异面直线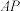 与
与 的夹角的余弦值为( )
的夹角的余弦值为( )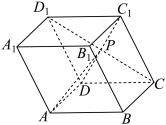
A. | B.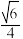 | C.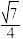 | D.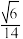 |
您最近一年使用:0次
2024-08-27更新
|
2186次组卷
|
11卷引用:湖北省武汉市武昌实验中学2024-2025学年高二上学期10月月考数学试卷
湖北省武汉市武昌实验中学2024-2025学年高二上学期10月月考数学试卷江苏省宿迁市泗洪县2023-2024学年高二下学期期中数学试题安徽省合肥市第一中学滨湖校区2024-2025学年高二上学期素质拓展训练(一)数学试卷(已下线)第2题 多法搞定异面直线所成的角(高二同步9月刊)福建省部分优质高中2024-2025学年高二上学期第一次阶段性质量检测数学试卷河南省开封市龙亭区河南大学附属中学2024-2025学年高二上学期10月月考数学试题山东省青岛市第九中学2024-2025学年高二上学期第一次阶段检测数学试卷广东省广州市培英中学2024-2025学年高二上学期10月学情调查数学试题广东省清远市阳山县南阳中学2024-2025学年高二上学期第一次月考数学试题甘肃省陇南市礼县第一中学2024-2025学年高二上学期第二次月考数学试题河南省新乡市河南师范大学附属中学2024-2025学年高二上学期10月月考数学试卷
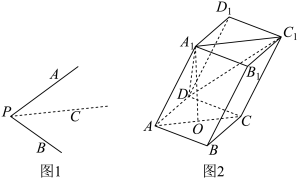
8 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记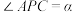 ,
,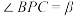 ,
, ,二面角
,二面角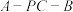 的大小为
的大小为 ,则
,则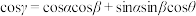 .如图2,四棱柱
.如图2,四棱柱 中,
中,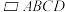 为菱形,
为菱形, ,
,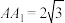 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.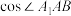 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: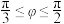 ;
;
(3)过点 作平面
作平面 ,使平面
,使平面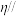 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记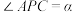 ,
,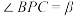 ,
, ,二面角
,二面角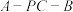 的大小为
的大小为 ,则
,则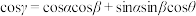 .如图2,四棱柱
.如图2,四棱柱 中,
中,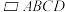 为菱形,
为菱形, ,
,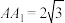 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
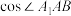 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: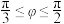 ;
;(3)过点
 作平面
作平面 ,使平面
,使平面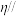 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
您最近一年使用:0次
2024-07-20更新
|
782次组卷
|
6卷引用:湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题
湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题山东省德州市夏津育中万隆中英文高级中学2024-2025学年高二上学期第一次月考数学试题山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2(已下线)拔高点突破04 新情景、新定义下的立体几何问题(六大题型)-1
9 . 四面体 中,
中,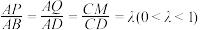 ,平面
,平面 交
交 于点
于点 ,则下列结论正确的是( )
,则下列结论正确的是( )
 中,
中,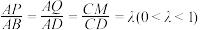 ,平面
,平面 交
交 于点
于点 ,则下列结论正确的是( )
,则下列结论正确的是( )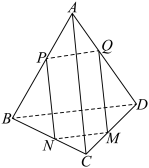
A.四边形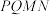 可以不是平行四边形 可以不是平行四边形 |
B.四边形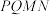 是矩形的充要条件是 是矩形的充要条件是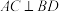 |
C.当 时,四边形 时,四边形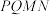 的面积最大 的面积最大 |
D.当 时,截面 时,截面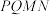 刚好平分四面体 刚好平分四面体 的体积 的体积 |
您最近一年使用:0次
10 . 如图,已知二面角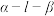 的平面角为
的平面角为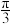 ,棱
,棱 上有不同的两点
上有不同的两点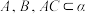 ,
, ,
, ,
,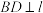 .若
.若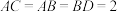 ,则下列结论正确的是( )
,则下列结论正确的是( )
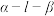 的平面角为
的平面角为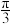 ,棱
,棱 上有不同的两点
上有不同的两点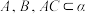 ,
, ,
, ,
,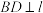 .若
.若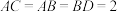 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.点 到平面 到平面 的距离是2 的距离是2 |
B.直线 与直线 与直线 的夹角为 的夹角为 |
C.四面体 的体积为 的体积为 |
D.过 四点的球的表面积为 四点的球的表面积为 |
您最近一年使用:0次



