名校
解题方法
1 . 下列命题中正确的是( )
A.已知函数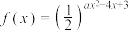 ,若函数 ,若函数 在区间 在区间 上是增函数,则 上是增函数,则 的取值范围是 的取值范围是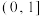 |
B.已知定义在 上的偶函数 上的偶函数 在 在 上单调递增,且 上单调递增,且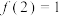 ,若 ,若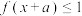 对 对 恒成立,则实数 恒成立,则实数 的取值范围是 的取值范围是 |
C.函数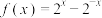 ,若不等式 ,若不等式 对 对 恒成立,则 恒成立,则 范围为 范围为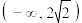 . . |
D.函数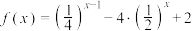 在 在 上的值域为 上的值域为 |
您最近一年使用:0次
名校
2 . 已知函数 ,
, .
.
(1)若 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得函数
,使得函数 与函数
与函数 的图象在区间
的图象在区间 上有唯一的交点,若存在,求出
上有唯一的交点,若存在,求出 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
 ,
, .
.(1)若
 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围;
的取值范围;(2)在(1)的条件下,是否存在实数
 ,使得函数
,使得函数 与函数
与函数 的图象在区间
的图象在区间 上有唯一的交点,若存在,求出
上有唯一的交点,若存在,求出 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
您最近一年使用:0次
2022-02-17更新
|
606次组卷
|
4卷引用:广东省茂名市化州市第一中学2021-2022学年高一下学期期中数学试题
名校
3 . 已知函数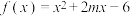 在区间
在区间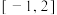 上是单调函数.
上是单调函数.
(1)求实数 的所有取值组成的集合
的所有取值组成的集合 ;
;
(2)试写出 在区间
在区间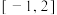 上的最大值
上的最大值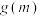 ;
;
(3)设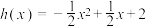 ,令
,令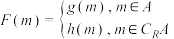 ,若对任意
,若对任意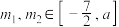 ,总有
,总有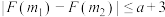 ,求
,求 的取值范围.
的取值范围.
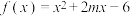 在区间
在区间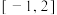 上是单调函数.
上是单调函数.(1)求实数
 的所有取值组成的集合
的所有取值组成的集合 ;
;(2)试写出
 在区间
在区间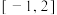 上的最大值
上的最大值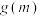 ;
;(3)设
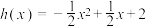 ,令
,令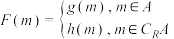 ,若对任意
,若对任意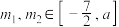 ,总有
,总有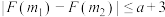 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2019-11-19更新
|
597次组卷
|
2卷引用:浙江省浙东北联盟(ZDB)2019-2020学年高一上学期期中数学试题
4 . 对于两条平行直线 、
、 (
( 在
在 下方)和图象
下方)和图象 有如下操作:将图象
有如下操作:将图象 在直线
在直线 下方的部分沿直线
下方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象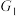 ;将图象
;将图象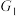 在直线
在直线 上方的部分沿直线
上方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象 :再将图
:再将图 在直线下方的部分沿直线
在直线下方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象 ;再将图象
;再将图象 在直线
在直线 上方的部分沿直线
上方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象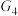 ;以此类推…;直到图象
;以此类推…;直到图象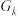 上所有点均在
上所有点均在 、
、 之间(含
之间(含 、
、 上)操作停止,此时称图象
上)操作停止,此时称图象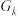 为图象
为图象 关于直线
关于直线 、
、 的“衍生图形”,线段
的“衍生图形”,线段 关于直线
关于直线 、
、 的“衍生图形”为折线段
的“衍生图形”为折线段 .
.
(1)直线型
平面直角坐标系中,设直线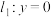 ,直线
,直线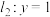
①令图象 为
为 的函数图象,则图象
的函数图象,则图象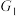 的解析式为
的解析式为
②令图像 为
为 的函数图象,请你画出
的函数图象,请你画出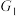 和
和 的图象
的图象
③若函数 的图象与图象
的图象与图象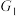 有且仅有一个交点,且交点在
有且仅有一个交点,且交点在 轴的左侧,那么
轴的左侧,那么 的取值范围是_______.
的取值范围是_______.
④请你观察图象 并描述其单调性,直接写出结果_______.
并描述其单调性,直接写出结果_______.
⑤请你观察图象 并判断其奇偶性,直接写出结果_______.
并判断其奇偶性,直接写出结果_______.
⑥图象 所对应函数的零点为_______.
所对应函数的零点为_______.
⑦任取图象 中横坐标
中横坐标 的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).
的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).
⑧若直线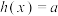 与图象
与图象 有2个不同的交点,则
有2个不同的交点,则 的取值范围是_______.
的取值范围是_______.
⑨根据函数图象,请你写出图象 的解析式_______.
的解析式_______.
(2)曲线型
若图象 为函数
为函数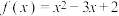 的图象,
的图象,
平面直角坐标系中,设直线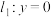 ,直线
,直线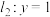 ,
,
则我们可以很容易得到 所对应的解析式为
所对应的解析式为 .
.
①请画出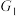 的图象,记
的图象,记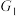 所对应的函数解析式为
所对应的函数解析式为 .
.
②函数 的单调增区间为_______,单调减区间为_______.
的单调增区间为_______,单调减区间为_______.
③当 时候,函数
时候,函数 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.
④若方程 有四个不同的实数根,则
有四个不同的实数根,则 的取值范围为_______.
的取值范围为_______.
(3)封闭图形型
平面直角坐标系中,设直线 ,直线
,直线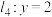
设图象 为四边形
为四边形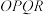 ,其顶点坐标分别为
,其顶点坐标分别为 ,
,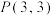 ,
,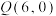 ,
, ,四边形
,四边形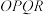 关于直线
关于直线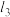 、
、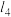 的“衍生图形”为
的“衍生图形”为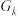 .
.
①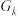 的周长为_______.
的周长为_______.
②若直线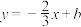 平分
平分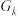 的周长,则
的周长,则 _______.
_______.
③将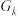 沿右上方
沿右上方 方向平移
方向平移 个单位,则平移过程中
个单位,则平移过程中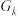 所扫过的面积为_______.
所扫过的面积为_______.
 、
、 (
( 在
在 下方)和图象
下方)和图象 有如下操作:将图象
有如下操作:将图象 在直线
在直线 下方的部分沿直线
下方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象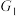 ;将图象
;将图象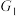 在直线
在直线 上方的部分沿直线
上方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象 :再将图
:再将图 在直线下方的部分沿直线
在直线下方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象 ;再将图象
;再将图象 在直线
在直线 上方的部分沿直线
上方的部分沿直线 翻折,其余部分保持不变,得到图象
翻折,其余部分保持不变,得到图象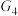 ;以此类推…;直到图象
;以此类推…;直到图象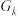 上所有点均在
上所有点均在 、
、 之间(含
之间(含 、
、 上)操作停止,此时称图象
上)操作停止,此时称图象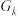 为图象
为图象 关于直线
关于直线 、
、 的“衍生图形”,线段
的“衍生图形”,线段 关于直线
关于直线 、
、 的“衍生图形”为折线段
的“衍生图形”为折线段 .
.(1)直线型
平面直角坐标系中,设直线
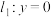 ,直线
,直线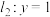
①令图象
 为
为 的函数图象,则图象
的函数图象,则图象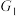 的解析式为
的解析式为②令图像
 为
为 的函数图象,请你画出
的函数图象,请你画出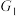 和
和 的图象
的图象
③若函数
 的图象与图象
的图象与图象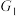 有且仅有一个交点,且交点在
有且仅有一个交点,且交点在 轴的左侧,那么
轴的左侧,那么 的取值范围是_______.
的取值范围是_______.④请你观察图象
 并描述其单调性,直接写出结果_______.
并描述其单调性,直接写出结果_______.⑤请你观察图象
 并判断其奇偶性,直接写出结果_______.
并判断其奇偶性,直接写出结果_______.⑥图象
 所对应函数的零点为_______.
所对应函数的零点为_______.⑦任取图象
 中横坐标
中横坐标 的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).
的点,那么在这个变化范围中所能取到的最高点的坐标为(_______,_______),最低点坐标为(_______,_______).⑧若直线
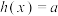 与图象
与图象 有2个不同的交点,则
有2个不同的交点,则 的取值范围是_______.
的取值范围是_______.⑨根据函数图象,请你写出图象
 的解析式_______.
的解析式_______.(2)曲线型
若图象
 为函数
为函数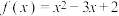 的图象,
的图象,平面直角坐标系中,设直线
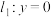 ,直线
,直线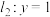 ,
,则我们可以很容易得到
 所对应的解析式为
所对应的解析式为 .
.
①请画出
 的图象,记
的图象,记 所对应的函数解析式为
所对应的函数解析式为 .
.②函数
 的单调增区间为_______,单调减区间为_______.
的单调增区间为_______,单调减区间为_______.③当
 时候,函数
时候,函数 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.④若方程
 有四个不同的实数根,则
有四个不同的实数根,则 的取值范围为_______.
的取值范围为_______.(3)封闭图形型
平面直角坐标系中,设直线
 ,直线
,直线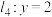
设图象
 为四边形
为四边形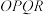 ,其顶点坐标分别为
,其顶点坐标分别为 ,
,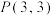 ,
,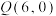 ,
, ,四边形
,四边形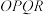 关于直线
关于直线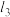 、
、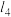 的“衍生图形”为
的“衍生图形”为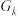 .
.①
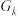 的周长为_______.
的周长为_______.②若直线
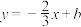 平分
平分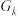 的周长,则
的周长,则 _______.
_______.③将
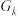 沿右上方
沿右上方 方向平移
方向平移 个单位,则平移过程中
个单位,则平移过程中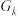 所扫过的面积为_______.
所扫过的面积为_______.
您最近一年使用:0次
5 . 对于在区间 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的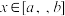 ,均有
,均有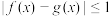 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.
(1)若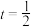 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合 ;
;
(3)在(2)的条件下,是否存在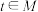 ,使得
,使得 与
与 在给定区间
在给定区间 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的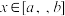 ,均有
,均有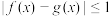 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.(1)若
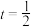 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;(2)若
 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合 ;
;
(3)在(2)的条件下,是否存在
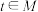 ,使得
,使得 与
与 在给定区间
在给定区间 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
6 . 设 ,已知函数
,已知函数 的表达式为
的表达式为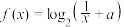 .
.
(1)当 时,求不等式
时,求不等式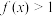 的解集;
的解集;
(2)设 ,若存在
,若存在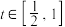 ,使得函数
,使得函数 在区间
在区间 上的最大值与最小值的差不超过1,求实数
上的最大值与最小值的差不超过1,求实数 的取值范围.
的取值范围.
 ,已知函数
,已知函数 的表达式为
的表达式为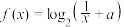 .
.(1)当
 时,求不等式
时,求不等式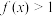 的解集;
的解集;(2)设
 ,若存在
,若存在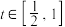 ,使得函数
,使得函数 在区间
在区间 上的最大值与最小值的差不超过1,求实数
上的最大值与最小值的差不超过1,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
7 . 已知函数
(1)若 ,写出函数
,写出函数 在
在 上的单调区间,并求
上的单调区间,并求 在
在 内的最小值;
内的最小值;
(2)设关于对 的不等式
的不等式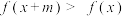 的解集为 A,且
的解集为 A,且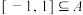 ,求实数
,求实数 的取值范围.
的取值范围.

(1)若
 ,写出函数
,写出函数 在
在 上的单调区间,并求
上的单调区间,并求 在
在 内的最小值;
内的最小值;(2)设关于对
 的不等式
的不等式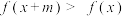 的解集为 A,且
的解集为 A,且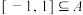 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-27更新
|
473次组卷
|
2卷引用:江苏省苏州中学校2023-2024学年高一上学期期中数学试卷
名校
解题方法
8 . 已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,解不等式
时,解不等式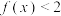 的解集;
的解集;
(2)当 时,写出函数
时,写出函数 的单调区间;
的单调区间;
(3)若在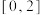 上存在
上存在 个不同的实数
个不同的实数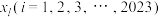 ,
, ,使得
,使得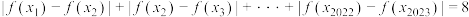 ,求实数
,求实数 的取值范围.
的取值范围.
 ,其中
,其中 为常数.
为常数.(1)当
 时,解不等式
时,解不等式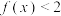 的解集;
的解集;(2)当
 时,写出函数
时,写出函数 的单调区间;
的单调区间;(3)若在
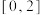 上存在
上存在 个不同的实数
个不同的实数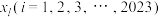 ,
, ,使得
,使得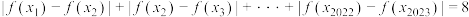 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-17更新
|
434次组卷
|
2卷引用:湖北省十堰市示范高中教联体测评联盟2023-2024学年高一上学期11月联考数学试题
名校
9 . 已知函数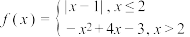 ,则下列说法正确的是( )
,则下列说法正确的是( )
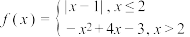 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若 的图象与直线 的图象与直线 有三个交点,则实数 有三个交点,则实数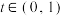 |
B.若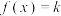 有三个不同实数根 有三个不同实数根 ,则 ,则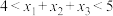 |
C.不等式 的解集是 的解集是 |
D.若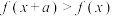 对任意实数x恒成立,则实数a的取值范围是 对任意实数x恒成立,则实数a的取值范围是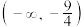 |
您最近一年使用:0次
2023-11-14更新
|
847次组卷
|
3卷引用:浙江省宁波市六校联盟2023-2024学年高一上学期11月期中数学试题
名校
解题方法
10 . 设 ,
, ,函数
,函数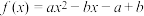 .
.
(1)求不等式 的解集;
的解集;
(2)若 在
在 上的最大值为
上的最大值为 ,求
,求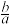 的取值范围;
的取值范围;
(3)当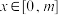 时,对任意的正实数
时,对任意的正实数 ,
, ,不等式
,不等式 恒成立,求
恒成立,求 的最大值.
的最大值.
 ,
, ,函数
,函数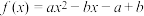 .
.(1)求不等式
 的解集;
的解集;(2)若
 在
在 上的最大值为
上的最大值为 ,求
,求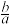 的取值范围;
的取值范围;(3)当
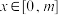 时,对任意的正实数
时,对任意的正实数 ,
, ,不等式
,不等式 恒成立,求
恒成立,求 的最大值.
的最大值.
您最近一年使用:0次



