名校
1 . 定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数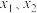 ,且
,且 ,都有
,都有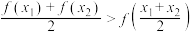 ,则称函数
,则称函数 在区间D上具有性质L.
在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)判断函数 在区间
在区间 上是否具有性质L?并用所给定义证明你的结论.
上是否具有性质L?并用所给定义证明你的结论.
(3)若函数 在区间
在区间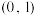 上具有性质L,求实数a的取值范围.
上具有性质L,求实数a的取值范围.
 在某一区间D上任取两个实数
在某一区间D上任取两个实数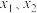 ,且
,且 ,都有
,都有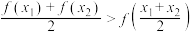 ,则称函数
,则称函数 在区间D上具有性质L.
在区间D上具有性质L.(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)判断函数
 在区间
在区间 上是否具有性质L?并用所给定义证明你的结论.
上是否具有性质L?并用所给定义证明你的结论.(3)若函数
 在区间
在区间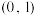 上具有性质L,求实数a的取值范围.
上具有性质L,求实数a的取值范围.
您最近一年使用:0次
真题
名校
2 . 已知函数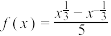 ,
,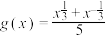 .
.
(1)求证: 是奇函数并求
是奇函数并求 的单调区间;
的单调区间;
(2)分别计算 合
合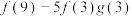 的值,由此概括出涉及函数
的值,由此概括出涉及函数 和
和 的对所有不等于零的实数
的对所有不等于零的实数 都成立的一个式,并加以证明.
都成立的一个式,并加以证明.
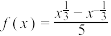 ,
,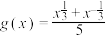 .
.(1)求证:
 是奇函数并求
是奇函数并求 的单调区间;
的单调区间;(2)分别计算
 合
合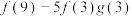 的值,由此概括出涉及函数
的值,由此概括出涉及函数 和
和 的对所有不等于零的实数
的对所有不等于零的实数 都成立的一个式,并加以证明.
都成立的一个式,并加以证明.
您最近一年使用:0次
2019-10-30更新
|
390次组卷
|
3卷引用:沪教版 高一年级第一学期 领航者 第四章 4.1幂函数的性质与图像(2)
3 . 设函数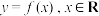 对任意的实数
对任意的实数 、
、 都有
都有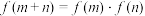 ,且当
,且当 时,
时,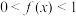 .
.
(1)在你学过的函数中,有没有满足上述条件的函数?若有,试举一例;
(2)试探求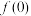 的值,并写出过程;
的值,并写出过程;
(3)求证:当 时,
时,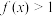 ;
;
(4)试猜想 的单调性,并证明你的结论.
的单调性,并证明你的结论.
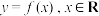 对任意的实数
对任意的实数 、
、 都有
都有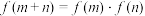 ,且当
,且当 时,
时,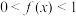 .
.(1)在你学过的函数中,有没有满足上述条件的函数?若有,试举一例;
(2)试探求
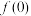 的值,并写出过程;
的值,并写出过程;(3)求证:当
 时,
时,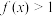 ;
;(4)试猜想
 的单调性,并证明你的结论.
的单调性,并证明你的结论.
您最近一年使用:0次
名校
4 . 对于正整数集合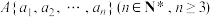 ,如果去掉其中任意一个元素
,如果去掉其中任意一个元素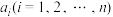 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“和谐集”.
为“和谐集”.
( )判断集合
)判断集合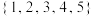 是否是“和谐集”(不必写过程).
是否是“和谐集”(不必写过程).
( )请写出一个只含有
)请写出一个只含有 个元素的“和谐集”,并证明此集合为“和谐集”.
个元素的“和谐集”,并证明此集合为“和谐集”.
( )当
)当 时,集合
时,集合 ,求证:集合
,求证:集合 不是“和谐集”.
不是“和谐集”.
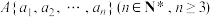 ,如果去掉其中任意一个元素
,如果去掉其中任意一个元素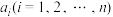 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合 为“和谐集”.
为“和谐集”.(
 )判断集合
)判断集合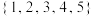 是否是“和谐集”(不必写过程).
是否是“和谐集”(不必写过程).(
 )请写出一个只含有
)请写出一个只含有 个元素的“和谐集”,并证明此集合为“和谐集”.
个元素的“和谐集”,并证明此集合为“和谐集”.(
 )当
)当 时,集合
时,集合 ,求证:集合
,求证:集合 不是“和谐集”.
不是“和谐集”.
您最近一年使用:0次
2018-07-02更新
|
1554次组卷
|
8卷引用:【全国百强校】北京东城北京二中2017-2018学年高二上学期期中考试数学(理)试题
【全国百强校】北京东城北京二中2017-2018学年高二上学期期中考试数学(理)试题人教A版(2019) 必修第一册 突围者 第一章 易错疑难集训(一)(已下线)1.2集合间的基本关系-2021-2022学年高一数学同步辅导讲义与检测(人教A版2019必修第一册)北京市西城区北京师范大学第二附属中学2021-2022学年高一上学期期中数学试题北京市大峪中学2022-2023学年高一上学期期中考试数学试题(已下线)高一上学期期中【压轴60题考点专练】(必修一前三章)-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)北京市人大附中北京经济技术开发区学校2023-2024学年高一上学期期中考试数学试题(已下线)期中真题必刷压轴60题(15个考点专练)-【满分全攻略】(人教A版2019必修第一册)
5 . 如果函数 在区间I上是减函数,而函数
在区间I上是减函数,而函数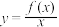 在区间I上是增函数,那么称函数
在区间I上是增函数,那么称函数 是区间I上“缓减函数”,区间I叫“缓减区间”.可以证明函数
是区间I上“缓减函数”,区间I叫“缓减区间”.可以证明函数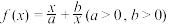 的单调增区间为
的单调增区间为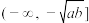 ,
,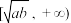 ;单调减区间为
;单调减区间为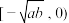 ,
,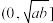 .若函数
.若函数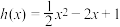 是区间I上“缓减函数”,则下列区间中为函数
是区间I上“缓减函数”,则下列区间中为函数 的“缓减函数区间”的是( )
的“缓减函数区间”的是( )
 在区间I上是减函数,而函数
在区间I上是减函数,而函数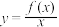 在区间I上是增函数,那么称函数
在区间I上是增函数,那么称函数 是区间I上“缓减函数”,区间I叫“缓减区间”.可以证明函数
是区间I上“缓减函数”,区间I叫“缓减区间”.可以证明函数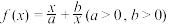 的单调增区间为
的单调增区间为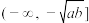 ,
,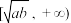 ;单调减区间为
;单调减区间为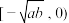 ,
,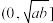 .若函数
.若函数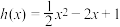 是区间I上“缓减函数”,则下列区间中为函数
是区间I上“缓减函数”,则下列区间中为函数 的“缓减函数区间”的是( )
的“缓减函数区间”的是( )A. | B.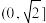 |
C.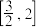 | D.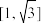 |
您最近一年使用:0次
名校
解题方法
6 . 已知函数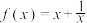 ,当
,当 时,
时, 的图象如图.
的图象如图.
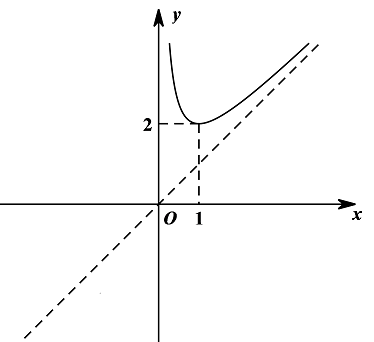
(1)判断并证明函数 的奇偶性;
的奇偶性;
(2)写出函数 的单调区间(直接写出结果);
的单调区间(直接写出结果);
(3)试讨论函数 在区间
在区间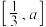 上的最大值.
上的最大值.
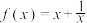 ,当
,当 时,
时, 的图象如图.
的图象如图.
(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)写出函数
 的单调区间(直接写出结果);
的单调区间(直接写出结果);(3)试讨论函数
 在区间
在区间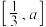 上的最大值.
上的最大值.
您最近一年使用:0次
名校
解题方法
7 . 已知函数 的定义域为
的定义域为 ,且对任意
,且对任意 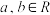 ,都有
,都有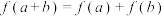 ,且当
,且当 时,
时,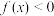 恒成立.
恒成立.
(1)证明:函数 是奇函数;
是奇函数;
(2) 在定义域上单调递减;
在定义域上单调递减;
(3) ,求
,求 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,且对任意
,且对任意 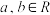 ,都有
,都有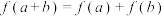 ,且当
,且当 时,
时,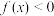 恒成立.
恒成立.(1)证明:函数
 是奇函数;
是奇函数;(2)
 在定义域上单调递减;
在定义域上单调递减;(3)
 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-09-07更新
|
3175次组卷
|
10卷引用:贵州省黔西南州同源中学2020-2021学年高一上学期期中教学质量检测数学试题
贵州省黔西南州同源中学2020-2021学年高一上学期期中教学质量检测数学试题河南省南阳市第一中学校2021-2022学年高一上学期第二次月考数学试题河南省实验中学2021-2022学年高一上学期期中数学试题黑龙江省绥化市第一中学2021-2022学年高一上学期期中数学试题(已下线)第三章 函数的概念和性质(章末复习)-【上好课】2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)第二章 函数 单元基础巩固试题-2021-2022学年高一数学上学期北师大版(2019)必修第一册第三章 函数的概念与性质 (B卷·提升能力)(已下线)人教A版高一上学期【期中押题卷01】-【满分全攻略】(人教A版2019必修第一册)陕西省咸阳市永寿县中学2023-2024学年高一上学期第二次月考数学试题(已下线)第5章 函数概念与性质 单元综合检测(重点)(单元培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)
15-16高一上·海南省直辖县级单位·期中
名校
8 . 已知函数 ,且
,且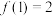 .
.
(1)证明函数 在
在 上是增函数;
上是增函数;
(2)求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
 ,且
,且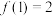 .
.(1)证明函数
 在
在 上是增函数;
上是增函数;(2)求函数
 在
在 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2020-10-30更新
|
1469次组卷
|
6卷引用:【南昌新东方】江西省南昌市南昌县莲塘一中2020-2021学年高一上学期第一次月考数学试题
(已下线)【南昌新东方】江西省南昌市南昌县莲塘一中2020-2021学年高一上学期第一次月考数学试题2015-2016学年海南省文昌中学高一上学期期中数学试卷广西桂林市临桂区五通中学2020-2021学年高一上学期期中考试数学试题重庆市万州纯阳中学校2021-2022学年高一上学期10月月考数学(A卷)试题(已下线)3.1.2 函数的单调性(2)黑龙江省大庆市大庆外国语学校2023-2024学年高一上学期期中数学试题
名校
解题方法
9 . 已知函数 是定义域为
是定义域为 上的奇函数.
上的奇函数.
(1)求 的值;
的值;
(2)用定义法证明函数的单调性,并求不等式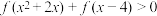 的解集;
的解集;
(3)若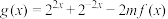 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
 是定义域为
是定义域为 上的奇函数.
上的奇函数.(1)求
 的值;
的值;(2)用定义法证明函数的单调性,并求不等式
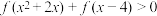 的解集;
的解集;(3)若
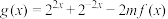 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
您最近一年使用:0次
2021-02-02更新
|
1157次组卷
|
6卷引用:沪教版(2020) 一轮复习 堂堂清 第二单元 综合练习(一)
沪教版(2020) 一轮复习 堂堂清 第二单元 综合练习(一)上海市实验学校2020-2021学年高一上学期期末数学试题(已下线)第19讲 函数的基本性质-单调性-【A+课堂】2021-2022学年高一数学同步精讲精练(沪教版2020必修第一册)(已下线)专题10 函数中的典型题(二)-【尖子生专用】2021-2022学年高一数学考点培优训练(人教A版2019必修第一册)(已下线)第5章 函数的概念、性质及应用(基础、典型、易错、压轴)分项训练-2022-2023学年高一数学考试满分全攻略(沪教版2020必修一)(已下线)知识点10 函数的单调性与奇偶性-2021-2022学年高一数学同步精品课堂讲+例+测(苏教版2019必修第一册)
解题方法
10 . 已知函数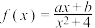 为定义在
为定义在 上的奇函数,且
上的奇函数,且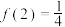 .
.
(1)求 、
、 的值;
的值;
(2)证明:函数 在区间
在区间 单调递增;
单调递增;
(3)当 时,函数
时,函数 在区间
在区间 上的值域为
上的值域为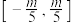 ,求实数
,求实数 的值.
的值.
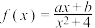 为定义在
为定义在 上的奇函数,且
上的奇函数,且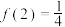 .
.(1)求
 、
、 的值;
的值;(2)证明:函数
 在区间
在区间 单调递增;
单调递增;(3)当
 时,函数
时,函数 在区间
在区间 上的值域为
上的值域为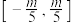 ,求实数
,求实数 的值.
的值.
您最近一年使用:0次



