名校
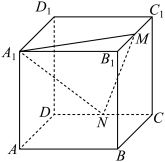
1 . 如图,在正方体 中,点M,N分别为棱
中,点M,N分别为棱 上的动点(包含端点),则下列说法正确的是
上的动点(包含端点),则下列说法正确的是_____________ .
①当M为棱 的中点时,则在棱
的中点时,则在棱 上存在点N使得
上存在点N使得 ;
;
②当M,N分别为棱 的中点时,则在正方体中存在棱与平面
的中点时,则在正方体中存在棱与平面 平行;
平行;
③当M,N分别为棱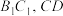 的中点时,则过
的中点时,则过 ,M,N三点作正方体的截面,所得截面为五边形;
,M,N三点作正方体的截面,所得截面为五边形;
④若正方体的棱长为2,则三棱锥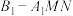 的体积可能为1;
的体积可能为1;
⑤直线 与平面
与平面 所成角的正切值的最小值为
所成角的正切值的最小值为 .
.
 中,点M,N分别为棱
中,点M,N分别为棱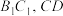 上的动点(包含端点),则下列说法正确的是
上的动点(包含端点),则下列说法正确的是
①当M为棱
 的中点时,则在棱
的中点时,则在棱 上存在点N使得
上存在点N使得 ;
;②当M,N分别为棱
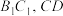 的中点时,则在正方体中存在棱与平面
的中点时,则在正方体中存在棱与平面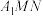 平行;
平行;③当M,N分别为棱
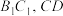 的中点时,则过
的中点时,则过 ,M,N三点作正方体的截面,所得截面为五边形;
,M,N三点作正方体的截面,所得截面为五边形;④若正方体的棱长为2,则三棱锥
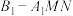 的体积可能为1;
的体积可能为1;⑤直线
 与平面
与平面 所成角的正切值的最小值为
所成角的正切值的最小值为 .
.
您最近一年使用:0次
2021-12-13更新
|
909次组卷
|
2卷引用:山西省晋城市第一中学2021-2022学年高二上学期第五次调研数学试题
解题方法
2 . 已知点P是直线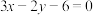 上的动点,过点P作圆
上的动点,过点P作圆 的切线,切点分别是A,B,则直线AB恒过定点的坐标为
的切线,切点分别是A,B,则直线AB恒过定点的坐标为___________ .
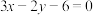 上的动点,过点P作圆
上的动点,过点P作圆 的切线,切点分别是A,B,则直线AB恒过定点的坐标为
的切线,切点分别是A,B,则直线AB恒过定点的坐标为
您最近一年使用:0次
2021-11-18更新
|
1309次组卷
|
4卷引用:山西省太原市2021-2022学年高二上学期期中质量监测数学试题
山西省太原市2021-2022学年高二上学期期中质量监测数学试题 山西省太原市第六十六中学校2021-2022学年高二上学期期中数学试题(已下线)陕西省西安市铁一中学2023-2024学年高三上学期第二次月考理科数学试题变式题15-18(已下线)专题7-1 直线与圆综合应用归类-2
名校
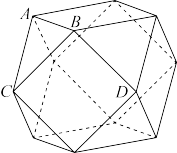
3 . “阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共截去八个三棱锥,得到的半正多面体的表面积为 ,则关于该半正多面体的下列说法中正确的是( )
,则关于该半正多面体的下列说法中正确的是( )
 ,则关于该半正多面体的下列说法中正确的是( )
,则关于该半正多面体的下列说法中正确的是( )
| A.与AB所成的角是60°的棱共有8条 |
| B.AB与平面BCD所成的角为30° |
C.二面角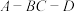 的余弦值为 的余弦值为 |
D.经过A,B,C,D四个顶点的球面面积为 |
您最近一年使用:0次
2021-09-10更新
|
815次组卷
|
5卷引用:山西省运城市康杰中学2021-2022学年高二上学期入学测试数学试题
山西省运城市康杰中学2021-2022学年高二上学期入学测试数学试题广东省深圳市第三高级中学2022届高三上学期9月第一次月考数学试题广东省广州市二中2021-2022学年高二上学期期中数学试题(已下线)第九章 立体几何专练10—二面角小题2-2022届高三数学一轮复习上海交通大学附属中学2023届高三下学期期中数学试题
名校
解题方法
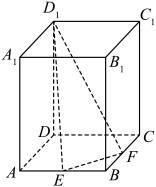
4 . 如图,直四棱柱 的底面是边长为2的正方形,
的底面是边长为2的正方形, ,
, ,
, 分别是
分别是 ,
, 的中点,过点
的中点,过点 ,
, ,
, 的平面记为
的平面记为 ,则下列说法中错误的是( )
,则下列说法中错误的是( )
 的底面是边长为2的正方形,
的底面是边长为2的正方形, ,
, ,
, 分别是
分别是 ,
, 的中点,过点
的中点,过点 ,
, ,
, 的平面记为
的平面记为 ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.点 到平面 到平面 的距离与点 的距离与点 到平面的距离之比为1:2 到平面的距离之比为1:2 |
B.平面 截直四棱柱 截直四棱柱 所得截面的面积为 所得截面的面积为 |
C.平面 将直四棱柱分割成的上、下两部分的体积之比为47:25 将直四棱柱分割成的上、下两部分的体积之比为47:25 |
D.平面 截直四棱柱 截直四棱柱 所得截面的形状为四边形 所得截面的形状为四边形 |
您最近一年使用:0次
名校
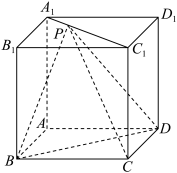
5 . 如图,在正方体 中,点P为线段
中,点P为线段 上的动点(点
上的动点(点 与
与 ,
, 不重合),则下列说法不正确的是( )
不重合),则下列说法不正确的是( )
 中,点P为线段
中,点P为线段 上的动点(点
上的动点(点 与
与 ,
, 不重合),则下列说法不正确的是( )
不重合),则下列说法不正确的是( )
A. |
B.三棱锥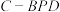 的体积为定值 的体积为定值 |
C.过 , , , , 三点作正方体的截面,截面图形为三角形或梯形 三点作正方体的截面,截面图形为三角形或梯形 |
D.DP与平面 所成角的正弦值最大为 所成角的正弦值最大为 |
您最近一年使用:0次
2021-09-06更新
|
2146次组卷
|
7卷引用:山西省大同市灵丘县豪洋中学2022届高三上学期开学摸底联考数学(理)试题
山西省大同市灵丘县豪洋中学2022届高三上学期开学摸底联考数学(理)试题山西省大同市灵丘县2022届高三上学期8月开学摸底联考数学(理)试题百师联盟2022届高三上学期开学摸底联考(全国1卷)数学(理)试题(已下线)专题8-2 立体几何截面问题的十种题型-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)(已下线)专题18 立体几何空间距离与截面100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)(已下线)专题23 立体几何中的压轴小题-1新疆克拉玛依市高级中学2021-2022学年高一年级 5 月月考数学试题
6 . 已知三棱锥 中,
中,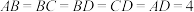 ,二面角
,二面角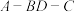 的余弦值为
的余弦值为 ,点
,点 在棱
在棱 上,且
上,且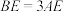 ,过
,过 作三棱锥
作三棱锥 外接球的截面,则所作截面面积的最小值为( )
外接球的截面,则所作截面面积的最小值为( )
 中,
中,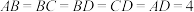 ,二面角
,二面角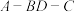 的余弦值为
的余弦值为 ,点
,点 在棱
在棱 上,且
上,且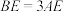 ,过
,过 作三棱锥
作三棱锥 外接球的截面,则所作截面面积的最小值为( )
外接球的截面,则所作截面面积的最小值为( )A.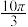 | B. | C. | D. |
您最近一年使用:0次
名校
解题方法
7 . 在正四棱锥 中,已知
中,已知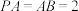 ,
, 为底面
为底面 的中心,以点
的中心,以点 为球心作一个半径为
为球心作一个半径为 的球,则该球的球面与侧面
的球,则该球的球面与侧面 的交线长度为( )
的交线长度为( )
 中,已知
中,已知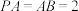 ,
, 为底面
为底面 的中心,以点
的中心,以点 为球心作一个半径为
为球心作一个半径为 的球,则该球的球面与侧面
的球,则该球的球面与侧面 的交线长度为( )
的交线长度为( )A.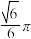 | B.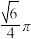 | C.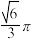 | D.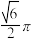 |
您最近一年使用:0次
2021-05-11更新
|
2144次组卷
|
5卷引用:山西省晋中市2021届高三三模数学(理)试题
山西省晋中市2021届高三三模数学(理)试题湖北省武汉市蔡甸区汉阳一中2021届高三仿真模拟(六)数学试题(已下线)第29讲 外接球与内切球问题-2022年新高考数学二轮专题突破精练(已下线)专题23 立体几何中的压轴小题-2黑龙江省齐齐哈尔市部分地区3校2023届高三上学期期中数学试题
8 . 攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称为攒尖.依其平面有圆形攒尖,三角攒尖、四角攒尖、六角攒尖等,也四有单檐和重檐之分,多见于亭阁式建筑.如图所示.某园林建筑屋顶为六角攒尖,它的主轮廓可近似看作一个正六棱锥(底面为正六边形,从顶点向底面作垂线,垂足是底面中心).若正六棱锥的侧棱与高线所成的角为 ,则其外接球半径与侧棱长的比值为( )
,则其外接球半径与侧棱长的比值为( )

 ,则其外接球半径与侧棱长的比值为( )
,则其外接球半径与侧棱长的比值为( )
A. | B.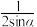 | C.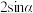 | D.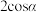 |
您最近一年使用:0次
2021-03-14更新
|
1955次组卷
|
10卷引用:山西省朔州市怀仁市2020-2021学年高一下学期期末数学试题
山西省朔州市怀仁市2020-2021学年高一下学期期末数学试题河南省2021届普通高中毕业班高考适应性测试数学(文)试题(已下线)专题8.1 基本立体图形及其直观图(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)专题39 仿真模拟卷05-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题36 仿真模拟卷05-2021年高考数学(文)二轮复习热点题型精选精练(已下线)专题10 立体几何-备战2021年高考数学(文)经典小题考前必刷集合(已下线)解密14 空间中的平行与垂直(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练(已下线)专题8.1 与数学文化相关的数学考题-玩转压轴题,进军满分之2021高考数学选择题填空题(已下线)专题一 点、直线和平面之间的位置关系-2021-2022学年高二数学同步单元AB卷(人教A版2019选择性必修第一册)(已下线)2020年高考全国1数学理高考真题变式题1-5题
2021·全国·模拟预测
9 . 已知在菱形 中,
中,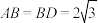 ,将菱形
,将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,且使得棱
,且使得棱 ,则三棱锥
,则三棱锥 的外接球的表面积为( )
的外接球的表面积为( )
 中,
中,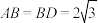 ,将菱形
,将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,且使得棱
,且使得棱 ,则三棱锥
,则三棱锥 的外接球的表面积为( )
的外接球的表面积为( )A.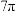 | B.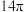 | C. | D.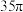 |
您最近一年使用:0次
2021-03-03更新
|
2236次组卷
|
6卷引用:山西省运城市新康国际实验学校2020-2021学年高二下学期4月测试数学(理)试题
山西省运城市新康国际实验学校2020-2021学年高二下学期4月测试数学(理)试题(已下线)2021新高考普通高等学校招生全国统一考试数学考向卷(一)(已下线)专题06 空间几何体的表面积与体积-备战2021年高考数学二轮复习题型专练(新高考专用)福建省泉州一中、莆田二中、仙游一中2020-2021学年高一下学期期中联考数学试题(已下线)第九章立体几何专练16—翻折问题-2022届高三数学一轮复习(已下线)高一数学下学期期中精选50题(压轴版)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)
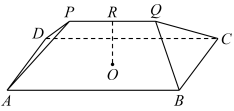
10 . 《九章算术》是古代中国的第一部自成体系的数学专著,与古希腊欧几里得的《几何原本》并称现代数学的两大源泉.《九章算术》卷五记载:“今有刍甍,下广三丈,表四丈,上袤二丈,无广,高一丈.问积几何?”译文:今有如图所示的屋脊状楔体 ,下底面
,下底面 是矩形,假设屋脊没有歪斜,即
是矩形,假设屋脊没有歪斜,即 的中点
的中点 在底面
在底面 上的投影为矩形
上的投影为矩形 的中心点
的中心点 ,
, ,
, ,
, ,
, ,
,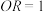 (长度单位:丈).则楔体
(长度单位:丈).则楔体 的体积为
的体积为___________ (体积单位:立方丈).
 ,下底面
,下底面 是矩形,假设屋脊没有歪斜,即
是矩形,假设屋脊没有歪斜,即 的中点
的中点 在底面
在底面 上的投影为矩形
上的投影为矩形 的中心点
的中心点 ,
, ,
, ,
, ,
, ,
,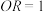 (长度单位:丈).则楔体
(长度单位:丈).则楔体 的体积为
的体积为
您最近一年使用:0次
2021-02-22更新
|
1744次组卷
|
9卷引用:山西省运城市高中联合体2021届高三下学期4月模拟数学(文)数学试题
山西省运城市高中联合体2021届高三下学期4月模拟数学(文)数学试题湖北省武汉市武昌区2020-2021学年高三上学期1月质量检测数学试题江苏省无锡市天一中学2021届高三下学期二模考前热身模拟数学试题(已下线) 专题18 几何体的表面积与体积的求解 (测)-2021年高三数学二轮复习讲练测(新高考版)(已下线) 专题22 几何体的表面积与体积的求解 (测)-2021年高三数学二轮复习讲练测(文理通用)(已下线)押第16题 立体几何综合-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)考点40 空间几何体-备战2021年高考数学经典小题考前必刷(新高考地区专用)重庆市凤鸣山中学2021届高三下学期第一次月考数学试题湖北省黄石市大冶市第一中学2021-2022学年高二上学期9月月考数学试题



