1 . 已知三棱柱 (如图所示),底面
(如图所示),底面 是边长为2的正三角形,侧棱
是边长为2的正三角形,侧棱 底面
底面 ,
,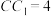 ,
, 为
为 的中点.
的中点. 为
为 的中点,求证:
的中点,求证: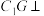 平面
平面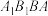 ;
;
(2)证明: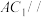 平面
平面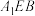 ;
;
(3)求三棱锥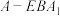 的体积.
的体积.
 (如图所示),底面
(如图所示),底面 是边长为2的正三角形,侧棱
是边长为2的正三角形,侧棱 底面
底面 ,
,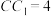 ,
, 为
为 的中点.
的中点.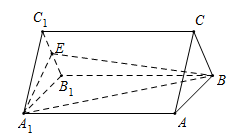
 为
为 的中点,求证:
的中点,求证: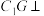 平面
平面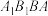 ;
;(2)证明:
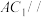 平面
平面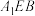 ;
;(3)求三棱锥
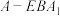 的体积.
的体积.
您最近一年使用:0次
2020-09-27更新
|
6471次组卷
|
16卷引用:山东省聊城市九校2020-2021学年高二上学期第一次开学联考数学试题
山东省聊城市九校2020-2021学年高二上学期第一次开学联考数学试题四川省成都市蓉城名校联盟2018-2019学年高一下学期期末联考数学试题四川省蓉城名校联盟2018-2019学年高一下学期期末数学(文)试题安徽省阜阳市太和第一中学2020-2021学年高二(普通班)上学期期中数学试题安徽省阜阳市太和第一中学2020-2021学年高二(奥赛班)上学期期中数学试题宁夏吴忠市吴忠中学2020-2021学年高二3月月考数学(文)试题云南省昆明市官渡区第一中学2021-2022学年高二上学期开学考数学试题河南省新乡市辉县市第一高级中学2020-2021学年高一下学期第一次阶段性考试数学试题(已下线)期末考测试(提升)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)安徽省六安第一中学2021-2022学年高一下学期期中数学试题(已下线)高一下学期数学期末考试高分押题密卷(二)-《考点·题型·密卷》河南市柘城县德盛高级中学2022-2023学年高一下学期6月月考数学试题 新疆哈密市第八中学2021-2022学年高二上学期期末考试数学(文)试题陕西省宝鸡市扶风县法门高中2023-2024学年高一下学期期中考试数学试卷陕西省咸阳市武功县普集高级中学2023-2024学年高一下学期第3次月考数学试题黑龙江省牡丹江市第二高级中学2023-2024学年高一下学期第二次月考数学试卷
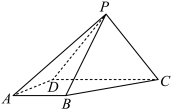
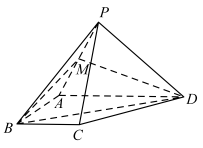
2 . 如图,在四棱锥P-ABCD中,平面PCD⊥平面ABCD,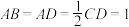 ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,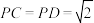 .
.
(1)求证:平面PAD⊥平面PBC;
(2)求直线PB与平面PAD所成的角;
(3)在棱PC上是否存在一点E使得直线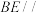 平面PAD,若存在求PE的长,并证明你的结论.
平面PAD,若存在求PE的长,并证明你的结论.
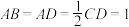 ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,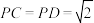 .
.
(1)求证:平面PAD⊥平面PBC;
(2)求直线PB与平面PAD所成的角;
(3)在棱PC上是否存在一点E使得直线
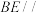 平面PAD,若存在求PE的长,并证明你的结论.
平面PAD,若存在求PE的长,并证明你的结论.
您最近一年使用:0次
名校
解题方法
3 . 如图,已知长方体 中,
中,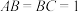 ,
,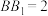 ,连接
,连接 ,过B点作
,过B点作 的垂线交
的垂线交 于E,交
于E,交 于F.
于F.

(1)求证: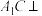 平面
平面 ;
;
(2)求点A到平面 的距离;
的距离;
 中,
中,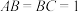 ,
,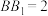 ,连接
,连接 ,过B点作
,过B点作 的垂线交
的垂线交 于E,交
于E,交 于F.
于F.
(1)求证:
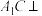 平面
平面 ;
;(2)求点A到平面
 的距离;
的距离;
您最近一年使用:0次
2023-10-19更新
|
766次组卷
|
5卷引用:【全国百强校】河北省遵化市堡子店中学2017-2018学年高二下学期期末考试(文科)数学试题
名校
解题方法
4 . 已知圆 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)若点 的坐标为
的坐标为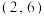 ,求直线
,求直线 的方程;
的方程;
(2)求证:直线 恒过定点
恒过定点 ,并求出该定点
,并求出该定点 的坐标.
的坐标.
 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.(1)若点
 的坐标为
的坐标为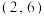 ,求直线
,求直线 的方程;
的方程;(2)求证:直线
 恒过定点
恒过定点 ,并求出该定点
,并求出该定点 的坐标.
的坐标.
您最近一年使用:0次
2022-12-05更新
|
433次组卷
|
3卷引用:山东省聊城市2020-2021学年第一学期高二期中考试数学试题
12-13高一下·安徽宿州·期末
名校
解题方法
5 . 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.求证:
(2)平面EFA1 平面BCHG.
平面BCHG.

(2)平面EFA1
 平面BCHG.
平面BCHG.
您最近一年使用:0次
2023-03-10更新
|
3709次组卷
|
69卷引用:2012-2013学年安徽省泗县双语中学高一下学期期末考试数学试卷
(已下线)2012-2013学年安徽省泗县双语中学高一下学期期末考试数学试卷2014-2015学年四川省中江县龙台中学高二上学期期中文科数学试卷2016-2017学年安徽合肥一中高二上月考一数学(文)试卷2016-2017学年湖南师大附中高一上学期段测三数学试卷湖北省宜昌市长阳一中2017-2018学年高二(上)9月月考数学(文科)试题【校级联考】江苏省淮安市高中校协作体2018~2019学年高二第一学期期中考试数学试题四川省绵阳中学2018-2019学年高一下学期第三次月考数学试题贵州省遵义市航天高级中学2019-2020学年高二上学期第一次月考数学试题江苏省无锡市辅仁高级中学2018-2019学年高一下学期期中数学试题贵州省遵义市汇川区航天高级中学2019-2020学年高二上学期期中数学试题(已下线)2019年11月9日 《每日一题》必修2-周末培优(已下线)2019年11月11日 《每日一题》必修2-平面与平面平行的判定(已下线)专题8.4 直线、平面平行的判定及其性质(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题8.4 直线、平面平行的判定及其性质(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题8.4 直线、平面平行的判定及其性质(讲)-浙江版《2020年高考一轮复习讲练测》甘肃省天水一中2019-2020学年高一上学期第二次段考数学试题陕西省延安市黄陵中学高新部2019-2020学年高一上学期期末数学试题(已下线)专题8.4 直线、平面平行的判定及其性质(讲)-江苏版《2020年高考一轮复习讲练测》安徽省淮北师范大学附中2019-2020学年高一上学期期末数学试题河北省武邑中学2019-2020学年高二上学期期中考试数学试题人教B版 必修2 必杀技 第一章 1.2.2空间中的平行关系课时3 平面与平面平行人教A版(2019) 必修第二册 必杀技 第8章 8.5.3 平面与平面平行四川省射洪县射洪中学2019-2020学年高二上学期入学考试数学试题(已下线)专题12 空间直线、平面的平行(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 专题强化练1 空间中的平行关系+专题强化练2 空间中的垂直关系(已下线)考点22 空间几何平行问题(讲解)-2021年高考数学复习一轮复习笔记(已下线)考点37 直线、平面平行的判定与性质(考点)-备战2021年新高考数学一轮复习考点微专题甘肃省兰州市兰州东方中学2020-2021学年高二上学期期中数学理科试题(已下线)专题8.4 直线、平面平行的判定及性质(讲)-2021年新高考数学一轮复习讲练测河南省南阳市第四中学2020-2021学年高一上学期第二次月考数学试题山东省聊城市聊城第一中学2021-2022学年高一下学期数学检测试题(已下线)2.2.4 平面与平面平行的性质-2020-2021学年高一数学课时同步练(人教A版必修2)重庆市第七中学2020-2021学年高一下学期期中数学试题西藏自治区拉萨中学2020-2021学年高一下学期期中考试数学试题(已下线)专题34直线、平面平行的判定与性质-2022年(新高考)数学高频考点+重点题型(已下线)考点47 直线与平面、平面与平面平行-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】北师大版 必修2 过关斩将 第一章 立体几何初步 专题强化练1 异面直线所成的角的求法 强化练2 空间平行关系的证明山东省枣庄市2020-2021学年高一下学期期中数学试题广东省佛山市第三中学2021-202学年高二上学期第一次教学质量检测数学试题四川省峨眉第二中学校2021-2022学年高二上学期10月月考文科数学试题四川省内江市威远中学校2021-2022学年高二上学期期中考试数学(文科)试题青海省海南州中学2021-2022学年高二上学期第一次月考数学(理)试题宁夏银川市景博中学2022届高三上学期期中考试数学(文)试题(已下线)8.5 空间直线、平面的平行(精讲)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)第02讲 基本图形的位置关系(1)四川省绵阳中学2022-2023学年高二上学期入学考试数学(理)试题(已下线)第47讲 直线与平面、平面与平面平行(已下线)第03讲 直线、平面平行垂直的判定与性质(讲)湖北省襄阳市第四中学2021-2022学年高一下学期5月月考数学试题(已下线)第30讲 平面与平面平行(已下线)8.5.3 平面与平面平行(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)重点题型训练13:第6章平行关系、垂直关系-2020-2021学年北师大版(2019)高中数学必修第二册(已下线)第18讲 基本图形位置关系云南省玉溪第一中学2022-2023学年高一下学期期中考试数学试题(已下线)8.5.3 平面与平面平行(1)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行(精练)-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)(已下线)专题09 基本图形的平行与垂直-期中期末考点大串讲(苏教版2019必修第二册)广东省湛江市第二十一中学2022-2023学年高一下学期期中数学试题(已下线)第03讲 空间中平行、垂直问题10种常见考法归类(1)福建省三明市尤溪县第五中学等两校2021-2022学年高一下学期期中联考数学试题黑龙江省鹤岗市第一中学2022-2023学年高一下学期期中数学试题安徽省安庆九一六学校2022-2023学年高一下学期第四次调研考试数学试题云南省大理市大理白族自治州民族中学2023-2024学年高二上学期开学考试数学试题四川省射洪中学校2022-2023学年高二上学期1月月考数学(文)试题(已下线)艺体生一轮复习 第七章 立体几何 第33讲 空间中的平行关系【讲】 1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(文科)试题(十五)(已下线)8.5空间直线、平面的平行——课后作业(基础版)河南省郑州市优胜实验中学2023-2024学年高一下学期期中考试数学试卷(已下线)专题05 立体几何初步(2)-期末考点大串讲(苏教版(2019))
9-10高一下·山东滨州·期末
名校
解题方法
6 . 如图,已知在直三棱柱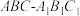 中(侧棱垂直于底面),
中(侧棱垂直于底面),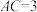 ,
,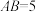 ,
, ,点
,点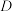 是
是 的中点.
的中点.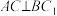 ;
;
(2)求证: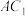
 平面
平面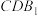 .
.
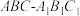 中(侧棱垂直于底面),
中(侧棱垂直于底面),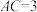 ,
,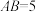 ,
, ,点
,点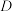 是
是 的中点.
的中点.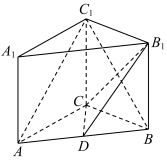
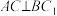 ;
;(2)求证:
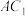
 平面
平面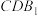 .
.
您最近一年使用:0次
2022-10-19更新
|
564次组卷
|
34卷引用:2010-2011年山东省莘县实验中学高一第一次阶段检测数学试卷
(已下线)2010-2011年山东省莘县实验中学高一第一次阶段检测数学试卷(已下线)2010年山东省阳信一中高一下学期期末考试数学卷(已下线)2011届北京市五中高三上学期期中考试数学文卷(已下线)2011-2012学年江苏省南通市通州区四星级中学高二期中联考数学试卷(已下线)2011-2012学年山东省梁山二中高二12月份月考文科数学试卷(已下线)2011-2012学年云南省蒙自高级中学高一上学期期末考试数学试卷(已下线)2011-2012学年广东省罗定市高二下学期期中质量检测文科数学试卷(已下线)2011-2012学年湖南省衡阳七校高一上期末质量检测数学试卷2015-2016学年湖北宜昌一中高二上学期期中理科数学试卷2015-2016学年山东省滕州市二中高一12月月考数学试卷2015-2016学年天津市河西区高二上学期期末理科数学试卷2015-2016学年陕西省黄陵中学高二上学期期末考试理科数学试卷2015-2016学年吉林毓文中学高一上期末数学试卷2016-2017学年安徽合肥一中高二上月考一数学(文)试卷新疆昌吉市2017-2018学年高二上学期期末考试数学(理)试题【全国校级联考】河北省石家庄市行唐县三中、正定县三中、正定县七中2017届高三10月联考数学(理)试题2018-2019人教A版高中数学选修2-1第三章 空间向量与立体几何 章末评估验收(三)【校级联考】河南省商丘市九校2018-2019学年高一上学期期末联考数学试题【校级联考】江西省南昌市八一中学、洪都中学、麻丘高中等七校2018-2019学年高二下学期期中考试数学(理)试题四川省南充市2018-2019学年高一下学期期末数学试题(B)广东省阳江市阳东广雅中学2019-2020学年高一上学期期末数学试题辽宁省营口市第二高级中学2018-2019学年高一下学期第一次月考数学试题福建省莆田第十五中学2019-2020学年高二上学期期末考试数学试题宁夏固原市隆德县2020-2021学年高二上学期期末考试数学(理)试题新疆哈密市第八中学2020-2021学年高二上学期期末考试数学试题宁夏吴忠中学2020-2021学年高二下学期期末数学(文)试题甘肃天水市第一中学2020-2021学年高二下学期学业水平测试第三模考试数学试题云南省昭通市昭阳区第一中学2020-2021学年高二下学期第一次月考数学(文)试题四川省遂宁中学校2020-2021学年高二下学期第一次月考数学(文)试题(已下线)复习题三1重庆市璧山来凤中学校2023届高三上学期10月月考数学(春招班)试题新疆阿克苏地区柯坪湖州国庆中学2021-2022学年高三上学期第一次月考数学试题(文)四川省乐山市草堂高级中学2022-2023学年高二上学期期中数学试题人教B版(2019) 选修第一册 北京名校同步练习册 第一章 空间向量与立体几何 1.2空间向量在立体几何中的应用 1.2.1空间中的点、直线与空间向量
名校
解题方法
7 . 如图,已知,四边形ABCD为长方形,平面PDC⊥平面ABCD,PD=PC=4,AB=6,BC=3.
(2)证明:求点C到平面PDA的距离.
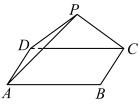
(2)证明:求点C到平面PDA的距离.
您最近一年使用:0次
2022-12-08更新
|
337次组卷
|
5卷引用:新疆乌鲁木齐市第四中学2019-2020学年高一下学期期末考试数学试题
新疆乌鲁木齐市第四中学2019-2020学年高一下学期期末考试数学试题山东省聊城第一中学2023-2024学年高一下学期第二次阶段性测试数学试题新疆巴音郭楞蒙古自治州第二中学2021届高三上学期开学第一次摸底考试数学(文)试题河南省安阳市第一中学2020-2021学年高一上学期期末数学试题(已下线)8.6.2 空间角与空间距离(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)
名校
解题方法
8 . 如图,在四棱锥 中,底面四边形
中,底面四边形 满足
满足 ,
,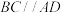 ,
,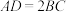 ,且
,且 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若平面 平面
平面 ,且
,且 ,求证:平面
,求证:平面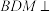 平面
平面 .
.
 中,底面四边形
中,底面四边形 满足
满足 ,
,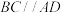 ,
,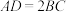 ,且
,且 为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)若平面
 平面
平面 ,且
,且 ,求证:平面
,求证:平面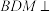 平面
平面 .
.
您最近一年使用:0次
2020-08-03更新
|
2279次组卷
|
7卷引用:山东省聊城市2019—2020学年度第二学期高一年级期末教学质量抽测数学试题
名校
解题方法
9 . 如图1所示, 为矩形,四边形
为矩形,四边形 为正方形.
为正方形. 与
与 为全等的等腰梯形,其中
为全等的等腰梯形,其中 ,沿着
,沿着 ,
, ,
, ,
,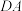 折成如图2所示的几何体
折成如图2所示的几何体 ,使
,使 ,
, ,
, ,
, 分别与
分别与 ,
, ,
, ,
, 重合.
重合.
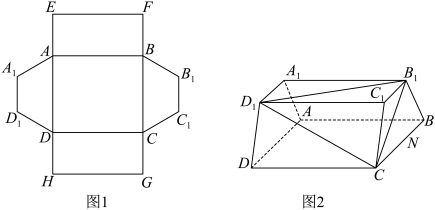
(1)求证:平面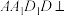 平面
平面 ;
;
(2)求平面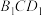 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 为矩形,四边形
为矩形,四边形 为正方形.
为正方形. 与
与 为全等的等腰梯形,其中
为全等的等腰梯形,其中 ,沿着
,沿着 ,
, ,
, ,
,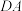 折成如图2所示的几何体
折成如图2所示的几何体 ,使
,使 ,
, ,
, ,
, 分别与
分别与 ,
, ,
, ,
, 重合.
重合.
(1)求证:平面
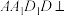 平面
平面 ;
;(2)求平面
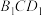 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
您最近一年使用:0次
2020-07-15更新
|
397次组卷
|
2卷引用:2020年山东省聊城市高考模拟考试(三模)数学试题
名校
10 . 如图,在三棱锥 中,
中,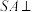 底面
底面 ,
,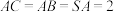 ,
, ,
, 分别是
分别是 的中点,F在SE 上,且
的中点,F在SE 上,且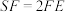 .
.
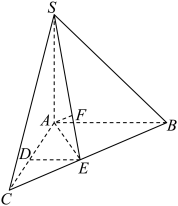
(1)求证: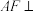 平面
平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 中,
中,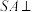 底面
底面 ,
,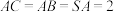 ,
, ,
, 分别是
分别是 的中点,F在SE 上,且
的中点,F在SE 上,且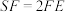 .
.
(1)求证:
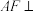 平面
平面 ;
;(2)在线段
 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
您最近一年使用:0次
2020-04-17更新
|
530次组卷
|
9卷引用:山东省聊城一中2019-2020学年高三4月份线上模拟试题
山东省聊城一中2019-2020学年高三4月份线上模拟试题浙江省嘉兴市第一中学2017届高三适应性考试数学试题浙江省嘉兴一中2017届高三适应性测试数学试题湖南省长郡中学2017-2018学年高二12月月考(第二次模块检测)数学(理)试题(已下线)专题8.3 空间点、直线、平面之间的位置关系(讲)-浙江版《2020年高考一轮复习讲练测》2020届山东省章丘市第四中学高三3月模拟考试数学试题湖南省衡阳市第八中学2019-2020学年高三上学期第四次月考数学(理)试题陕西省延安市第一中学2019-2020学年高二下学期6月月考数学(理)试题江西省宜春中学2021-2022学年高二下学期开学考数学(理)试题



