名校
解题方法
1 . 已知函数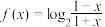 .
.
(1)判断并证明 的奇偶性;
的奇偶性;
(2)若对任意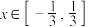 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
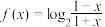 .
.(1)判断并证明
 的奇偶性;
的奇偶性;(2)若对任意
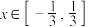 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
2024-09-12更新
|
2504次组卷
|
5卷引用:江苏省南通市2025届高三九月份调研考试数学试题
江苏省南通市2025届高三九月份调研考试数学试题安徽省六安第二中学2024-2025学年高三上学期第二次月考(10月)数学试题重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题(已下线)4.2.3 对数函数的性质与图象+4.3 指数函数与对数函数的关系——课后作业(提升版)山东省聊城第一中学2025届高三上学期第一次月考数学试题
名校
解题方法
2 . 已知在锐角 中,
中, ,
, 为
为 边上一点,且
边上一点,且 .
.
(1)证明: 平分
平分 ;
;
(2)已知 ,求
,求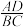 .
.
 中,
中, ,
, 为
为 边上一点,且
边上一点,且 .
.(1)证明:
 平分
平分 ;
;(2)已知
 ,求
,求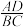 .
.
您最近一年使用:0次
2024-08-20更新
|
1710次组卷
|
2卷引用:广东省广州市2025届普通高中毕业班摸底考试数学试题
名校
解题方法
3 . 定义 ,
, 那么以下说法正确的有(填序号)
那么以下说法正确的有(填序号)______ .
A.
B.除了 以外,
以外, 都是奇数
都是奇数
C.对于任意的n,
D.以 ,
, ,
, 为三边的三角形是直角三角形
为三边的三角形是直角三角形
 ,
, 那么以下说法正确的有(填序号)
那么以下说法正确的有(填序号)A.

B.除了
 以外,
以外, 都是奇数
都是奇数C.对于任意的n,

D.以
 ,
, ,
, 为三边的三角形是直角三角形
为三边的三角形是直角三角形
您最近一年使用:0次
2024-08-10更新
|
245次组卷
|
2卷引用:2025届高三天枢杯第二届线上联考数学试题
名校
解题方法
4 . 已知数列 满足
满足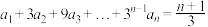 ,设数列
,设数列 的前
的前 项和为
项和为 ,则满足
,则满足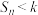 的实数
的实数 的最小值为
的最小值为__________ .
 满足
满足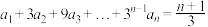 ,设数列
,设数列 的前
的前 项和为
项和为 ,则满足
,则满足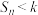 的实数
的实数 的最小值为
的最小值为
您最近一年使用:0次
2024-07-26更新
|
1557次组卷
|
3卷引用:广东省广州市2025届普通高中毕业班摸底考试数学试题
名校
解题方法
5 . 已知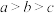 ,若
,若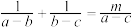 成立,则实数
成立,则实数 的最小值为( )
的最小值为( )
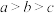 ,若
,若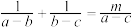 成立,则实数
成立,则实数 的最小值为( )
的最小值为( )| A.2 | B.3 | C.4 | D.5 |
您最近一年使用:0次
2024-06-14更新
|
1659次组卷
|
3卷引用:2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题
6 . 定义:在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”,例如:数列 经过第一次“和扩充”后得到数列
经过第一次“和扩充”后得到数列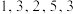 ;第二次“和扩充”后得到数列
;第二次“和扩充”后得到数列 .设数列
.设数列 经过
经过 次“和扩充”后得到的数列的项数为
次“和扩充”后得到的数列的项数为 ,所有项的和为
,所有项的和为 .
.
(1)若 ,求
,求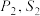 ;
;
(2)求不等式 的解集;
的解集;
(3)是否存在数列 ,使得数列
,使得数列 为等比数列?请说明理由.
为等比数列?请说明理由.
 经过第一次“和扩充”后得到数列
经过第一次“和扩充”后得到数列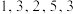 ;第二次“和扩充”后得到数列
;第二次“和扩充”后得到数列 .设数列
.设数列 经过
经过 次“和扩充”后得到的数列的项数为
次“和扩充”后得到的数列的项数为 ,所有项的和为
,所有项的和为 .
.(1)若
 ,求
,求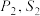 ;
;(2)求不等式
 的解集;
的解集;(3)是否存在数列
 ,使得数列
,使得数列 为等比数列?请说明理由.
为等比数列?请说明理由.
您最近一年使用:0次
2024-06-14更新
|
914次组卷
|
6卷引用:2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题
2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题河南省南阳市2023-2024学年高二下学期期末考前热身联考数学试题(已下线)第03讲 等比数列及其前n项和(九大题型)(讲义)-2(已下线)拔高点突破01 新情景、新定义下的数列问题(七大题型)山东省菏泽市2024届高三下学期模拟预测信息押题卷(一)数学试题(已下线)周测13数列通项公式、求和(一轮好卷基础卷)
名校
解题方法
7 . 在 中,内角A,B,C所对边分别为a,b,c,已知
中,内角A,B,C所对边分别为a,b,c,已知 .
.
(1)求角A的大小;
(2)若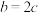 ,
, 的面积为
的面积为 ,求
,求 的周长.
的周长.
 中,内角A,B,C所对边分别为a,b,c,已知
中,内角A,B,C所对边分别为a,b,c,已知 .
.(1)求角A的大小;
(2)若
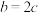 ,
, 的面积为
的面积为 ,求
,求 的周长.
的周长.
您最近一年使用:0次
7日内更新
|
1854次组卷
|
6卷引用:四川省南充市2025届高三高考适应性考试(一诊)数学试卷
四川省南充市2025届高三高考适应性考试(一诊)数学试卷云南省昆明市西南联大研究院附属学校2024-2025学年高二上学期10月月考数学试卷北京市陈经纶中学2025届高三上学期10月月考数学试题河北省保定市河北安国中学2024-2025学年高一下学期第一次月考数学试题(已下线)考点42 余弦定理及应用 --高考数学100个黄金考点(2025届)【练】(已下线)第01章 函数与方程的思想【提升版】
名校
8 . 我国数学著作《九章算术》中很早就有有关数列问题的记载:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”,译文为:“现有 人分
人分 钱(一种单位),要使分得钱数最多的两人所得的钱数和与其他三人所得的钱数和相等,且五人分得的钱数的某种排列成等差数列,问各得多少钱.”在上述问题中随机取一人,这个人得到的钱数可能为:
钱(一种单位),要使分得钱数最多的两人所得的钱数和与其他三人所得的钱数和相等,且五人分得的钱数的某种排列成等差数列,问各得多少钱.”在上述问题中随机取一人,这个人得到的钱数可能为:__________ .(写出一种可能即可).
 人分
人分 钱(一种单位),要使分得钱数最多的两人所得的钱数和与其他三人所得的钱数和相等,且五人分得的钱数的某种排列成等差数列,问各得多少钱.”在上述问题中随机取一人,这个人得到的钱数可能为:
钱(一种单位),要使分得钱数最多的两人所得的钱数和与其他三人所得的钱数和相等,且五人分得的钱数的某种排列成等差数列,问各得多少钱.”在上述问题中随机取一人,这个人得到的钱数可能为:
您最近一年使用:0次
名校
解题方法
9 . 已知 是各项均为正数的数列
是各项均为正数的数列 的前
的前 项和,
项和,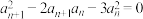 ,
, ,则数列
,则数列 的通项公式为
的通项公式为______ .
 是各项均为正数的数列
是各项均为正数的数列 的前
的前 项和,
项和,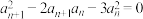 ,
, ,则数列
,则数列 的通项公式为
的通项公式为
您最近一年使用:0次
名校
解题方法
10 . 设 为数列,
为数列,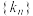 为正整数集
为正整数集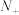 的无限子集,且
的无限子集,且 ,则数列
,则数列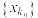 称为数列
称为数列 的一个子列.已知数列
的一个子列.已知数列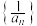 为等差数列,
为等差数列, 的某个子列
的某个子列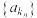 构成等比数列,若
构成等比数列,若 ,则数列
,则数列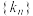 的前
的前 项和为:( ).
项和为:( ).
 为数列,
为数列,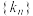 为正整数集
为正整数集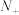 的无限子集,且
的无限子集,且 ,则数列
,则数列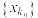 称为数列
称为数列 的一个子列.已知数列
的一个子列.已知数列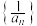 为等差数列,
为等差数列, 的某个子列
的某个子列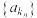 构成等比数列,若
构成等比数列,若 ,则数列
,则数列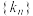 的前
的前 项和为:( ).
项和为:( ).A.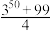 | B.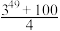 | C.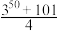 | D.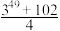 |
您最近一年使用:0次



