名校
1 . 我们可以把平面向量坐标的概念推广为“复向量”,即可将有序复数对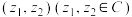 视为一个向量,记作
视为一个向量,记作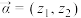 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量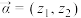 ,
, 的数量积记作
的数量积记作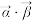 ,定义为
,定义为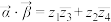 ;复向量
;复向量 的模定义为
的模定义为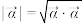 .
.
(1)设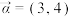 ,
,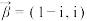 ,求复向量
,求复向量 与
与 的模;
的模;
(2)已知对任意的实向量 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;
①求证:对任意实数a,b,c,d,不等式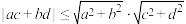 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;
②求证:对任意两个复向量 与
与 ,不等式
,不等式 仍然成立;
仍然成立;
(3)当 时,称复向量
时,称复向量 与
与 平行.设
平行.设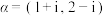 ,
,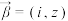 ,
,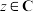 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
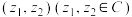 视为一个向量,记作
视为一个向量,记作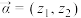 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量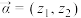 ,
, 的数量积记作
的数量积记作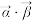 ,定义为
,定义为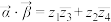 ;复向量
;复向量 的模定义为
的模定义为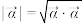 .
.(1)设
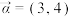 ,
,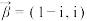 ,求复向量
,求复向量 与
与 的模;
的模;(2)已知对任意的实向量
 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;①求证:对任意实数a,b,c,d,不等式
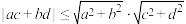 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;②求证:对任意两个复向量
 与
与 ,不等式
,不等式 仍然成立;
仍然成立;(3)当
 时,称复向量
时,称复向量 与
与 平行.设
平行.设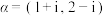 ,
,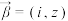 ,
,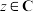 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
您最近一年使用:0次
2 . 有序数组是指数组里的数是按规定次序排列的,虽然仍然是同样一些数,但排列次序不同,看作是不同的数组.已知有序数组 :
: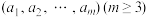 ,由此数组变换可得到一个新的有序数组
,由此数组变换可得到一个新的有序数组 :
: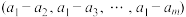 .如果有序数组
.如果有序数组 中的数满足:当
中的数满足:当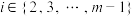 时,
时,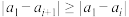 恒成立,则称有序数组
恒成立,则称有序数组 为“首差不减数组”.
为“首差不减数组”.
(1)已知有序数组P: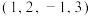 ,Q:
,Q: ,试判断有序数组P,Q是否为“首差不减数组”,并说明理由;
,试判断有序数组P,Q是否为“首差不减数组”,并说明理由;
(2)有序数组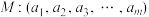 是数1,2,3,…,m的一个排列,有序数组
是数1,2,3,…,m的一个排列,有序数组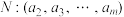 ,若有序数组M,N均为“首差不减数组”,列举出所有满足条件的有序数组M.
,若有序数组M,N均为“首差不减数组”,列举出所有满足条件的有序数组M.
 :
: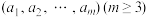 ,由此数组变换可得到一个新的有序数组
,由此数组变换可得到一个新的有序数组 :
: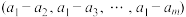 .如果有序数组
.如果有序数组 中的数满足:当
中的数满足:当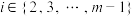 时,
时,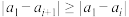 恒成立,则称有序数组
恒成立,则称有序数组 为“首差不减数组”.
为“首差不减数组”.(1)已知有序数组P:
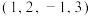 ,Q:
,Q: ,试判断有序数组P,Q是否为“首差不减数组”,并说明理由;
,试判断有序数组P,Q是否为“首差不减数组”,并说明理由;(2)有序数组
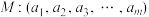 是数1,2,3,…,m的一个排列,有序数组
是数1,2,3,…,m的一个排列,有序数组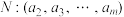 ,若有序数组M,N均为“首差不减数组”,列举出所有满足条件的有序数组M.
,若有序数组M,N均为“首差不减数组”,列举出所有满足条件的有序数组M.
您最近一年使用:0次
名校
3 . 函数 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点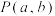 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数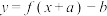 为奇函数.已知函数
为奇函数.已知函数 .
.
(1)若函数 的对称中心为
的对称中心为 ,求函数
,求函数 的解析式.
的解析式.
(2)由代数基本定理可以得到:任何一元 次复系数多项式
次复系数多项式 在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程
在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程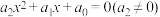 ,在复数集内的根为
,在复数集内的根为 ,
, ,则方程
,则方程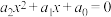 可变形为
可变形为 ,展开得:
,展开得: 则有
则有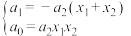 ,即
,即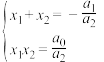 ,类比上述推理方法可得实系数一元三次方程根与系数的关系.
,类比上述推理方法可得实系数一元三次方程根与系数的关系.
①若 ,方程
,方程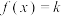 在复数集内的根为
在复数集内的根为 ,当
,当 时,求
时,求 的最大值;
的最大值;
②若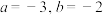 ,函数
,函数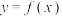 的零点分别为
的零点分别为 ,求
,求 的值.
的值.
 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点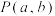 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数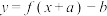 为奇函数.已知函数
为奇函数.已知函数 .
.(1)若函数
 的对称中心为
的对称中心为 ,求函数
,求函数 的解析式.
的解析式.(2)由代数基本定理可以得到:任何一元
 次复系数多项式
次复系数多项式 在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程
在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程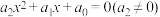 ,在复数集内的根为
,在复数集内的根为 ,
, ,则方程
,则方程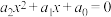 可变形为
可变形为 ,展开得:
,展开得: 则有
则有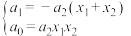 ,即
,即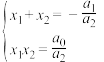 ,类比上述推理方法可得实系数一元三次方程根与系数的关系.
,类比上述推理方法可得实系数一元三次方程根与系数的关系.①若
 ,方程
,方程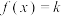 在复数集内的根为
在复数集内的根为 ,当
,当 时,求
时,求 的最大值;
的最大值;②若
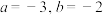 ,函数
,函数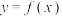 的零点分别为
的零点分别为 ,求
,求 的值.
的值.
您最近一年使用:0次
4 . 对于非空集合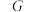 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在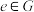 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得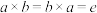 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意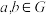 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群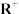 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群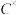 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
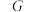 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
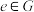 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得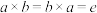 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意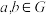 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
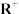 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群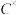 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近一年使用:0次
解题方法
5 . 设M是由复数组成的集合,对M的一个子集A,若存在复平面上的一个圆,使得A的所有数在复平面上对应的点都在圆内或圆周上,且 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
(1)判断 是否是
是否是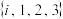 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;
(2)设复数z满足 ,其中
,其中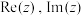 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: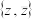 是
是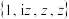 的“可分离子集”当且仅当
的“可分离子集”当且仅当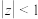 .
.
 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.(1)判断
 是否是
是否是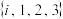 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;(2)设复数z满足
 ,其中
,其中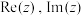 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: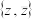 是
是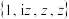 的“可分离子集”当且仅当
的“可分离子集”当且仅当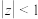 .
.
您最近一年使用:0次
6 . 已知 :
: 为有穷数列.若对任意的
为有穷数列.若对任意的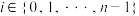 ,都有
,都有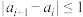 (规定
(规定 ),则称
),则称 具有性质
具有性质 .设
.设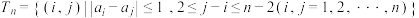 .
.
(1)判断数列 :1,0.1,-0.2,0.5,
:1,0.1,-0.2,0.5, :1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合
:1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合 ;
;
(2)若 具有性质
具有性质 ,证明:
,证明: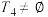 ;
;
(3)给定正整数 ,对所有具有性质
,对所有具有性质 的数列
的数列 ,求
,求 中元素个数的最小值.
中元素个数的最小值.
 :
: 为有穷数列.若对任意的
为有穷数列.若对任意的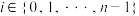 ,都有
,都有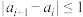 (规定
(规定 ),则称
),则称 具有性质
具有性质 .设
.设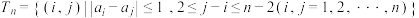 .
.(1)判断数列
 :1,0.1,-0.2,0.5,
:1,0.1,-0.2,0.5, :1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合
:1,2,0.7,1.2,2是否具有性质P?若具有性质P,写出对应的集合 ;
;(2)若
 具有性质
具有性质 ,证明:
,证明: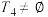 ;
;(3)给定正整数
 ,对所有具有性质
,对所有具有性质 的数列
的数列 ,求
,求 中元素个数的最小值.
中元素个数的最小值.
您最近一年使用:0次
2023-11-02更新
|
467次组卷
|
2卷引用:北京一零一中2023-2024学年高二上学期期中考试数学试题
7 . 设 为正整数,若
为正整数,若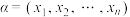 满足:①
满足:①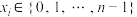 ,
, ,2,…,
,2,…, ;②对于
;②对于 ,均有
,均有 .则称
.则称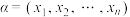 具有性质
具有性质 .对于
.对于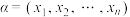 和
和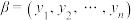 ,定义集合
,定义集合 .
.
(1)设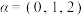 ,若
,若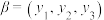 具有性质
具有性质 ,写出一个
,写出一个 及相应的
及相应的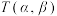 ;
;
(2)设 和
和 具有性质
具有性质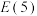 ,那么
,那么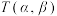 是否可能为
是否可能为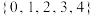 ,若可能,写出一组
,若可能,写出一组 和
和 ,若不可能,说明理由;
,若不可能,说明理由;
(3)设 和
和 具有性质
具有性质 ,对于给定的
,对于给定的 ,求证:满足
,求证:满足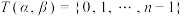 的
的 有偶数个.
有偶数个.
 为正整数,若
为正整数,若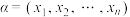 满足:①
满足:①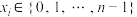 ,
, ,2,…,
,2,…, ;②对于
;②对于 ,均有
,均有 .则称
.则称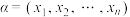 具有性质
具有性质 .对于
.对于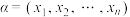 和
和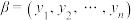 ,定义集合
,定义集合 .
.(1)设
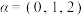 ,若
,若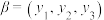 具有性质
具有性质 ,写出一个
,写出一个 及相应的
及相应的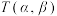 ;
;(2)设
 和
和 具有性质
具有性质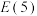 ,那么
,那么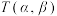 是否可能为
是否可能为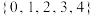 ,若可能,写出一组
,若可能,写出一组 和
和 ,若不可能,说明理由;
,若不可能,说明理由;(3)设
 和
和 具有性质
具有性质 ,对于给定的
,对于给定的 ,求证:满足
,求证:满足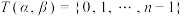 的
的 有偶数个.
有偶数个.
您最近一年使用:0次
8 . 若正整数 的二进制表示是
的二进制表示是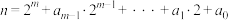 ,这里
,这里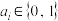 (
(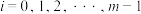 ),称有穷数列1,
),称有穷数列1,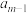 ,
, ,
, ,
, 为
为 的生成数列,设
的生成数列,设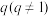 是一个给定的实数,称
是一个给定的实数,称 为
为 的生成数.
的生成数.
(1)求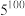 的生成数列的项数;
的生成数列的项数;
(2)求由 的生成数列
的生成数列 ,
, ,
, ,
, 的前
的前 项的和
项的和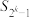 (用
(用 、
、 表示);
表示);
(3)若实数 满足
满足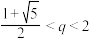 ,证明:存在无穷多个正整数
,证明:存在无穷多个正整数 ,使得不存在正整数
,使得不存在正整数 满足
满足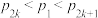 .
.
 的二进制表示是
的二进制表示是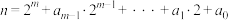 ,这里
,这里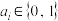 (
(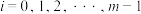 ),称有穷数列1,
),称有穷数列1,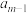 ,
, ,
, ,
, 为
为 的生成数列,设
的生成数列,设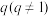 是一个给定的实数,称
是一个给定的实数,称 为
为 的生成数.
的生成数.(1)求
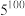 的生成数列的项数;
的生成数列的项数;(2)求由
 的生成数列
的生成数列 ,
, ,
, ,
, 的前
的前 项的和
项的和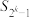 (用
(用 、
、 表示);
表示);(3)若实数
 满足
满足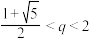 ,证明:存在无穷多个正整数
,证明:存在无穷多个正整数 ,使得不存在正整数
,使得不存在正整数 满足
满足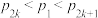 .
.
您最近一年使用:0次
9 . 对于无穷数列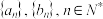 ,若
,若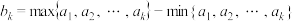 ,
,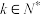 ,则称数列
,则称数列 是数列
是数列 的“收缩数列”,其中
的“收缩数列”,其中 分别表示
分别表示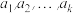 中的最大项和最小项,已知数列
中的最大项和最小项,已知数列 的前n项和为
的前n项和为 ,数列
,数列 是数列
是数列 的“收缩数列”
的“收缩数列”
(1)若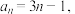 求数列
求数列 的前n项和;
的前n项和;
(2)证明:数列 的“收缩数列”仍是
的“收缩数列”仍是 ;
;
(3)若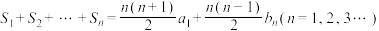 ,求所有满足该条件的数列
,求所有满足该条件的数列 .
.
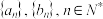 ,若
,若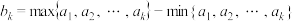 ,
,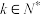 ,则称数列
,则称数列 是数列
是数列 的“收缩数列”,其中
的“收缩数列”,其中 分别表示
分别表示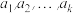 中的最大项和最小项,已知数列
中的最大项和最小项,已知数列 的前n项和为
的前n项和为 ,数列
,数列 是数列
是数列 的“收缩数列”
的“收缩数列”(1)若
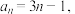 求数列
求数列 的前n项和;
的前n项和;(2)证明:数列
 的“收缩数列”仍是
的“收缩数列”仍是 ;
;(3)若
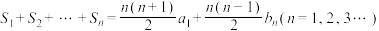 ,求所有满足该条件的数列
,求所有满足该条件的数列 .
.
您最近一年使用:0次
2020-09-03更新
|
1073次组卷
|
4卷引用:2020届上海市青浦区高三二模数学试题
10 . 已知函数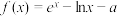 .
.
(1)若 .证明函数
.证明函数 有且仅有两个零点;
有且仅有两个零点;
(2)若函数 存在两个零点
存在两个零点 ,证明:
,证明: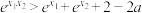 .
.
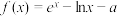 .
.(1)若
 .证明函数
.证明函数 有且仅有两个零点;
有且仅有两个零点;(2)若函数
 存在两个零点
存在两个零点 ,证明:
,证明: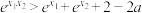 .
.
您最近一年使用:0次



