名校
解题方法
1 . 已知双曲线G的中心为坐标原点,离心率为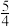 ,左、右顶点分别为
,左、右顶点分别为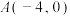 ,
,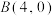 .
.
(1)求 的方程;
的方程;
(2)过右焦点 的直线l与G的右支交于M,N两点,若直线
的直线l与G的右支交于M,N两点,若直线 与
与 交于点
交于点 .
.
(i)证明:点 在定直线上:
在定直线上:
(ii)若直线 与
与 交于点
交于点 ,求证:
,求证: .
.
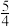 ,左、右顶点分别为
,左、右顶点分别为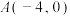 ,
,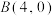 .
.(1)求
 的方程;
的方程;(2)过右焦点
 的直线l与G的右支交于M,N两点,若直线
的直线l与G的右支交于M,N两点,若直线 与
与 交于点
交于点 .
.(i)证明:点
 在定直线上:
在定直线上:(ii)若直线
 与
与 交于点
交于点 ,求证:
,求证: .
.
您最近一年使用:0次
2024-04-17更新
|
1114次组卷
|
2卷引用:辽宁省葫芦岛市2024届高三下学期第一次模拟数学试题
名校
2 . n个有次序的实数 ,
, ,…,
,…, 所组成的有序数组
所组成的有序数组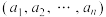 称为一个n维向量,其中
称为一个n维向量,其中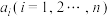 称为该向量的第i个分量.特别地,对一个n维向量
称为该向量的第i个分量.特别地,对一个n维向量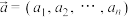 ,若
,若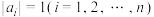 ,称
,称 为n维信号向量.设
为n维信号向量.设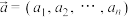 ,
,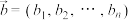 ,则
,则 和
和 的内积定义为
的内积定义为 ,且
,且 .
.
(1)直接写出4个两两垂直的4维信号向量;
(2)证明:不存在10个两两垂直的10维信号向量;
(3)已知k个两两垂直的2024维信号向量 ,
,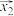 ,…,
,…,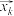 满足它们的前m个分量都是相同的,求证:
满足它们的前m个分量都是相同的,求证: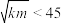 .
.
 ,
, ,…,
,…, 所组成的有序数组
所组成的有序数组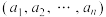 称为一个n维向量,其中
称为一个n维向量,其中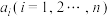 称为该向量的第i个分量.特别地,对一个n维向量
称为该向量的第i个分量.特别地,对一个n维向量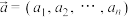 ,若
,若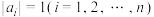 ,称
,称 为n维信号向量.设
为n维信号向量.设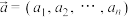 ,
,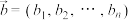 ,则
,则 和
和 的内积定义为
的内积定义为 ,且
,且 .
.(1)直接写出4个两两垂直的4维信号向量;
(2)证明:不存在10个两两垂直的10维信号向量;
(3)已知k个两两垂直的2024维信号向量
 ,
,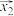 ,…,
,…,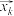 满足它们的前m个分量都是相同的,求证:
满足它们的前m个分量都是相同的,求证: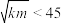 .
.
您最近一年使用:0次
22-23高二下·四川遂宁·阶段练习
3 . 已知抛物线C: ,过点
,过点 的直线l交抛物线交于A,B两点,抛物线在点A处的切线为
的直线l交抛物线交于A,B两点,抛物线在点A处的切线为 ,在点B处的切线为
,在点B处的切线为 ,直线
,直线 与
与 交于点M.
交于点M.
(1)设直线 ,
, 的斜率分别为直线
的斜率分别为直线 ,
, ,求证:
,求证: ;
;
(2)证明:点M在定直线上;
(3)设线段AB的中点为N,求 的取值范围.
的取值范围.
 ,过点
,过点 的直线l交抛物线交于A,B两点,抛物线在点A处的切线为
的直线l交抛物线交于A,B两点,抛物线在点A处的切线为 ,在点B处的切线为
,在点B处的切线为 ,直线
,直线 与
与 交于点M.
交于点M.(1)设直线
 ,
, 的斜率分别为直线
的斜率分别为直线 ,
, ,求证:
,求证: ;
;(2)证明:点M在定直线上;
(3)设线段AB的中点为N,求
 的取值范围.
的取值范围.
您最近一年使用:0次
名校
4 . 如图,在三棱柱 中,
中, 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 ,
, ,
, ,
, 的中点,
的中点,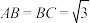 ,
, .
. 平面
平面 ;
;
(2)求平面 与直线
与直线 所成角的正弦值;
所成角的正弦值;
(3)证明:直线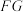 与平面
与平面 相交.
相交.
 中,
中, 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 ,
, ,
, ,
, 的中点,
的中点,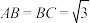 ,
, .
.
 平面
平面 ;
;(2)求平面
 与直线
与直线 所成角的正弦值;
所成角的正弦值;(3)证明:直线
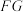 与平面
与平面 相交.
相交.
您最近一年使用:0次
5 . 已知椭圆 经过点
经过点 ,且焦距为
,且焦距为 .
.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左、右顶点分别为
的左、右顶点分别为 、
、 ,点
,点 为椭圆
为椭圆 上异于
上异于 、
、 的动点,设
的动点,设 交直线
交直线 于点
于点 ,连接
,连接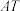 交椭圆
交椭圆 于点
于点 ,直线
,直线 的斜率分别为
的斜率分别为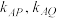 .
.
①求证: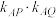 为定值;
为定值;
②证明:直线 经过
经过 轴上的定点,并求出该定点的坐标.
轴上的定点,并求出该定点的坐标.
 经过点
经过点 ,且焦距为
,且焦距为 .
.(1)求椭圆
 的方程;
的方程;(2)设椭圆
 的左、右顶点分别为
的左、右顶点分别为 、
、 ,点
,点 为椭圆
为椭圆 上异于
上异于 、
、 的动点,设
的动点,设 交直线
交直线 于点
于点 ,连接
,连接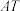 交椭圆
交椭圆 于点
于点 ,直线
,直线 的斜率分别为
的斜率分别为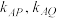 .
.①求证:
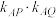 为定值;
为定值;②证明:直线
 经过
经过 轴上的定点,并求出该定点的坐标.
轴上的定点,并求出该定点的坐标.
您最近一年使用:0次
6 . 已知动圆 过定点
过定点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)已知 、
、 两点的坐标分别为
两点的坐标分别为 、
、 ,直线
,直线 、
、 的斜率分别为
的斜率分别为 、
、 ,证明:
,证明: ;
;
(2)若点 、
、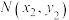 是轨迹
是轨迹 上的两个动点且
上的两个动点且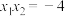 ,设线段
,设线段 的中点为
的中点为 ,圆
,圆 与动点
与动点 的轨迹
的轨迹 交于不同于
交于不同于 的三点
的三点 、
、 、
、 ,求证:
,求证: 的重心的横坐标为定值.
的重心的横坐标为定值.
 过定点
过定点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.(1)已知
 、
、 两点的坐标分别为
两点的坐标分别为 、
、 ,直线
,直线 、
、 的斜率分别为
的斜率分别为 、
、 ,证明:
,证明: ;
;(2)若点
 、
、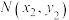 是轨迹
是轨迹 上的两个动点且
上的两个动点且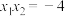 ,设线段
,设线段 的中点为
的中点为 ,圆
,圆 与动点
与动点 的轨迹
的轨迹 交于不同于
交于不同于 的三点
的三点 、
、 、
、 ,求证:
,求证: 的重心的横坐标为定值.
的重心的横坐标为定值.
您最近一年使用:0次
7 . 已知双曲线 的方程为
的方程为 ,虚轴长为2,点
,虚轴长为2,点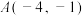 在
在 上.
上.
(1)求双曲线 的方程;
的方程;
(2)过原点 的直线与
的直线与 交于
交于 两点,已知直线
两点,已知直线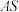 和直线
和直线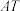 的斜率存在,证明:直线
的斜率存在,证明:直线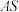 和直线
和直线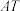 的斜率之积为定值;
的斜率之积为定值;
(3)过点 的直线交双曲线
的直线交双曲线 于
于 两点,直线
两点,直线 与
与 轴的交点分别为
轴的交点分别为 ,求证:
,求证: 的中点为定点.
的中点为定点.
 的方程为
的方程为 ,虚轴长为2,点
,虚轴长为2,点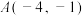 在
在 上.
上.(1)求双曲线
 的方程;
的方程;(2)过原点
 的直线与
的直线与 交于
交于 两点,已知直线
两点,已知直线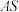 和直线
和直线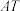 的斜率存在,证明:直线
的斜率存在,证明:直线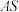 和直线
和直线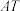 的斜率之积为定值;
的斜率之积为定值;(3)过点
 的直线交双曲线
的直线交双曲线 于
于 两点,直线
两点,直线 与
与 轴的交点分别为
轴的交点分别为 ,求证:
,求证: 的中点为定点.
的中点为定点.
您最近一年使用:0次
2024-03-03更新
|
1474次组卷
|
6卷引用:贵州省贵阳市2024届高三下学期适应性考试数学试卷(一)
2023·江苏·模拟预测
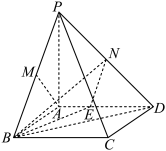
8 . 如图,在四棱锥 中,侧棱
中,侧棱 平面ABCD,底面四边形ABCD是矩形,
平面ABCD,底面四边形ABCD是矩形,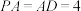 ,点M,N分别为棱PB,PD的中点,点E在棱AD上,
,点M,N分别为棱PB,PD的中点,点E在棱AD上,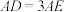 .
.
(1)求证:直线 平面BNE;
平面BNE;
(2)从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面PAB与平面PCD的交线l与直线BE所成角的余弦值为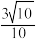 ;
;
②二面角 的余弦值为
的余弦值为 .
.
注:若选择不同的组合分别作答,则按第一个解答计分.
 中,侧棱
中,侧棱 平面ABCD,底面四边形ABCD是矩形,
平面ABCD,底面四边形ABCD是矩形,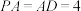 ,点M,N分别为棱PB,PD的中点,点E在棱AD上,
,点M,N分别为棱PB,PD的中点,点E在棱AD上,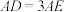 .
.
(1)求证:直线
 平面BNE;
平面BNE;(2)从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面PAB与平面PCD的交线l与直线BE所成角的余弦值为
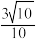 ;
;②二面角
 的余弦值为
的余弦值为 .
.注:若选择不同的组合分别作答,则按第一个解答计分.
您最近一年使用:0次
2023·安徽六安·模拟预测
名校
解题方法
9 . 已知点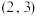 在双曲线
在双曲线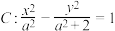 上.
上.
(1)双曲线上动点Q处的切线交 的两条渐近线于
的两条渐近线于 两点,其中O为坐标原点,求证:
两点,其中O为坐标原点,求证: 的面积
的面积 是定值;
是定值;
(2)已知点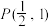 ,过点
,过点 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、 ,在线段
,在线段 上取异于点
上取异于点 、
、 的点
的点 ,满足
,满足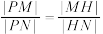 ,证明:点
,证明:点 恒在一条定直线上.
恒在一条定直线上.
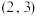 在双曲线
在双曲线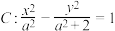 上.
上.(1)双曲线上动点Q处的切线交
 的两条渐近线于
的两条渐近线于 两点,其中O为坐标原点,求证:
两点,其中O为坐标原点,求证: 的面积
的面积 是定值;
是定值;(2)已知点
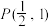 ,过点
,过点 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、 ,在线段
,在线段 上取异于点
上取异于点 、
、 的点
的点 ,满足
,满足 ,证明:点
,证明:点 恒在一条定直线上.
恒在一条定直线上.
您最近一年使用:0次
2023-05-17更新
|
1070次组卷
|
4卷引用:专题突破卷23 圆锥曲线大题归类
(已下线)专题突破卷23 圆锥曲线大题归类安徽省舒城中学2023届仿真模拟卷(二)数学试题(已下线)专题3.9 圆锥曲线中的定点、定值、定直线问题大题专项训练【九大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)山东省青岛市青岛第二中学2023-2024学年高二上学期期中数学试题
23-24高二上·上海·阶段练习
名校
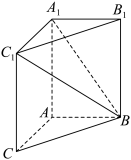
10 . 如图,在三棱柱 中,平面
中,平面 平面
平面 ,
, 边长为8的正方形,
边长为8的正方形,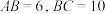 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)证明:在线段 上存在点
上存在点 ,使得
,使得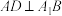 ,并求
,并求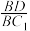 的值.
的值.
 中,平面
中,平面 平面
平面 ,
, 边长为8的正方形,
边长为8的正方形,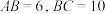 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)证明:在线段
 上存在点
上存在点 ,使得
,使得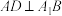 ,并求
,并求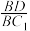 的值.
的值.
您最近一年使用:0次



