名校
1 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴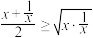 ,即
,即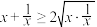 ,∴
,∴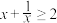 ,
,
当且仅当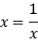 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①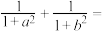 ___________.
___________.
②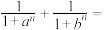 ___________.
___________.
(2)若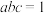 ,解方程
,解方程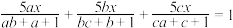 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴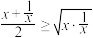 ,即
,即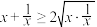 ,∴
,∴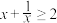 ,
,当且仅当
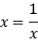 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
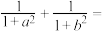 ___________.
___________.②
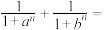 ___________.
___________.(2)若
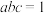 ,解方程
,解方程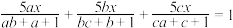 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2021-10-29更新
|
526次组卷
|
3卷引用:江苏省南通中学2020-2021学年高一上学期开学考试数学试题
江苏省南通中学2020-2021学年高一上学期开学考试数学试题江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
2 . 曲线的曲率定义如下:若 是
是 的导函数,令
的导函数,令 ,则曲线
,则曲线 在点
在点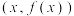 处的曲率
处的曲率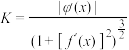 .已知函数
.已知函数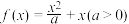 ,
, ,且
,且 在点
在点 处的曲率
处的曲率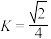 .
.
(1)求 的值,并证明:当
的值,并证明:当 时,
时, ;
;
(2)若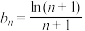 ,且
,且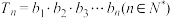 ,求证:
,求证: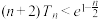 .
.
 是
是 的导函数,令
的导函数,令 ,则曲线
,则曲线 在点
在点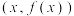 处的曲率
处的曲率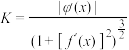 .已知函数
.已知函数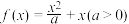 ,
, ,且
,且 在点
在点 处的曲率
处的曲率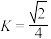 .
.(1)求
 的值,并证明:当
的值,并证明:当 时,
时, ;
;(2)若
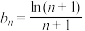 ,且
,且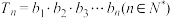 ,求证:
,求证: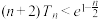 .
.
您最近一年使用:0次
2021-05-02更新
|
786次组卷
|
4卷引用:湖南省永州市2021届高三下学期三模数学试题
湖南省永州市2021届高三下学期三模数学试题(已下线)专题3.13 不等式的证明问题-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)第五篇 向量与几何 专题21 曲率与曲率圆 微点1 曲率与曲率圆(一)山西省晋城市第一中学校2024届高三上学期11月期中数学试题
名校
3 . 已知函数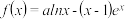 ,其中a为非零常数.
,其中a为非零常数.
 讨论
讨论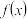 的极值点个数,并说明理由;
的极值点个数,并说明理由;
 若
若 ,
,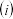 证明:
证明: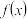 在区间
在区间 内有且仅有1个零点;
内有且仅有1个零点;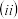 设
设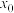 为
为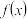 的极值点,
的极值点,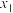 为
为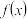 的零点且
的零点且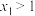 ,求证:
,求证: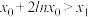 .
.
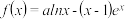 ,其中a为非零常数.
,其中a为非零常数. 讨论
讨论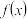 的极值点个数,并说明理由;
的极值点个数,并说明理由; 若
若 ,
,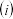 证明:
证明: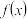 在区间
在区间 内有且仅有1个零点;
内有且仅有1个零点;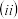 设
设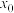 为
为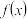 的极值点,
的极值点,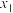 为
为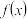 的零点且
的零点且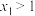 ,求证:
,求证: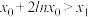 .
.
您最近一年使用:0次
2020-01-30更新
|
1028次组卷
|
7卷引用:2020届湖北省黄冈市高三上学期期末数学(理)试题
2020届湖北省黄冈市高三上学期期末数学(理)试题2020届湖北省第五届高考测评活动高三元月调考理科数学试题2020届广东省广州市执信中学高三2月月考数学(理)试题(已下线)必刷卷10-2020年高考数学必刷试卷(新高考)【学科网名师堂】-《2020年新高考政策解读与配套资源》2020届河南省平顶山市第一中学高三下学期开学检测(线上)文数试题安徽师范大学附属中学2019-2020学年高三下学期2月第一次月考理科数学试题(已下线)卷10-2020年高考数学冲刺逆袭必备卷(山东、海南专用)【学科网名师堂】
名校
4 . 已知函数 .
.
(1)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;
(2)当 时,求证:
时,求证: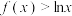 ;
;
(3)设函数 ,其中
,其中 为实常数,试讨论函数
为实常数,试讨论函数 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
 .
.(1)若曲线
 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;(2)当
 时,求证:
时,求证: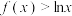 ;
;(3)设函数
 ,其中
,其中 为实常数,试讨论函数
为实常数,试讨论函数 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
您最近一年使用:0次
2019-12-30更新
|
1065次组卷
|
5卷引用:江苏省苏州市五校2019-2020学年高三上学期12月月考数学试卷
江苏省苏州市五校2019-2020学年高三上学期12月月考数学试卷2020届江苏省南京市十三中高三下学期期初考试数学试题(已下线)专题16 函数的零点-2021届江苏省新高考数学大讲坛大一轮复习天津市实验中学2022届高三下学期高考前热身训练数学试题天津市第四中学2023届高三高考热身数学试题
名校
5 . 已知函数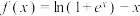 .
.
(Ⅰ)判断 零点的个数,并证明结论;
零点的个数,并证明结论;
(Ⅱ)已知 的三个顶点
的三个顶点 、
、 、
、 都在函数
都在函数 的图象上.且横坐标依次成等差数列,求证:
的图象上.且横坐标依次成等差数列,求证: 是钝角三角形.但不可能是等腰三角形.
是钝角三角形.但不可能是等腰三角形.
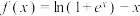 .
.(Ⅰ)判断
 零点的个数,并证明结论;
零点的个数,并证明结论;(Ⅱ)已知
 的三个顶点
的三个顶点 、
、 、
、 都在函数
都在函数 的图象上.且横坐标依次成等差数列,求证:
的图象上.且横坐标依次成等差数列,求证: 是钝角三角形.但不可能是等腰三角形.
是钝角三角形.但不可能是等腰三角形.
您最近一年使用:0次
名校
6 . 完成下列证明:
(Ⅰ)求证: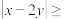
 ;
;
(Ⅱ)若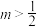 ,求证:
,求证: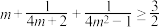 .
.
(Ⅰ)求证:
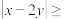
 ;
;(Ⅱ)若
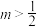 ,求证:
,求证: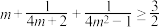 .
.
您最近一年使用:0次
2019-09-12更新
|
1114次组卷
|
3卷引用:江西省吉安市2018-2019学年高二下学期期末数学(理)试题
名校
解题方法
7 . 已知函数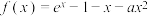 (
( ,
, 为自然对数的底数),
为自然对数的底数), 是
是 的导数.
的导数.
(1)当 时,求证:
时,求证: ;
;
(2)是否存在整数 ,使得
,使得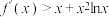 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的最大值,并证明你的结论;若不存在,也请说明理由.
的最大值,并证明你的结论;若不存在,也请说明理由.
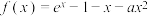 (
( ,
, 为自然对数的底数),
为自然对数的底数), 是
是 的导数.
的导数.(1)当
 时,求证:
时,求证: ;
;(2)是否存在整数
 ,使得
,使得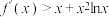 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的最大值,并证明你的结论;若不存在,也请说明理由.
的最大值,并证明你的结论;若不存在,也请说明理由.
您最近一年使用:0次
2020-03-22更新
|
427次组卷
|
4卷引用:2020届福建省福州第一中学高三下学期教学反馈检测数学(理)试题
2020届福建省福州第一中学高三下学期教学反馈检测数学(理)试题(已下线)2020届高三3月第01期(考点03)(理科)-《新题速递·数学》福建省福鼎第一中学2021-2022学年高二下学期第一次月考数学试题安徽省芜湖市第一中学2020届高三下学期3月第五次线上考试数学试题
名校
8 . 已知函数 ,其中
,其中 .
.
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)当 时,证明:
时,证明: ;
;
(Ⅲ)求证:对任意正整数n,都有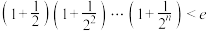 (其中e≈2.7183为自然对数的底数)
(其中e≈2.7183为自然对数的底数)
 ,其中
,其中 .
.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)当
 时,证明:
时,证明: ;
;(Ⅲ)求证:对任意正整数n,都有
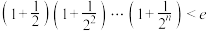 (其中e≈2.7183为自然对数的底数)
(其中e≈2.7183为自然对数的底数)
您最近一年使用:0次
2019-01-12更新
|
4101次组卷
|
10卷引用:【区级联考】天津市蓟州等部分区2019届高三上学期期末联考数学(文)试题
【区级联考】天津市蓟州等部分区2019届高三上学期期末联考数学(文)试题【区级联考】天津市部分区2019届高三(上)期末数学(文科)试题【全国百强校】四川省成都市成都外国语学校2018-2019学年高二下学期期中考试文科数学试题【全国百强校】河北省武邑中学2019届高三下学期第一次模拟考试数学(文)试题江西省五市八校2019-2020学年高三第二次联考文科数学试题湖北省武汉二中2019-2020学年高二下学期4月第二次线上测试数学试题四川省宜宾市第四中学校2019-2020学年高二下学期期中考试数学(理)试题四川省宜宾市第四中学校2019-2020学年高二下学期期中考试数学(文)试题广东省佛山市三水区三水中学2019-2020学年高二下学期第二次统考数学试题黑龙江省大庆实验中学2019届高三普通高等学校招生全国统一考试文科数学模拟试题
名校
9 . 用反证法证明命题①:“已知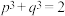 ,求证:
,求证: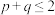 ”时,可假设“
”时,可假设“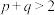 ”;命题②:“若
”;命题②:“若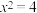 ,则
,则 或
或 ”时,可假设“
”时,可假设“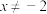 或
或 ”.以下结论正确的是
”.以下结论正确的是
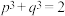 ,求证:
,求证: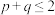 ”时,可假设“
”时,可假设“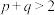 ”;命题②:“若
”;命题②:“若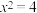 ,则
,则 或
或 ”时,可假设“
”时,可假设“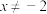 或
或 ”.以下结论正确的是
”.以下结论正确的是| A.①与②的假设都错误 | B.①与②的假设都正确 |
| C.①的假设正确,②的假设错误 | D.①的假设错误,②的假设正确 |
您最近一年使用:0次
2018-07-12更新
|
760次组卷
|
9卷引用:【全国市级联考】福建省三明市2017-2018学年高二下学期期末考试数学(文)试题
【全国市级联考】福建省三明市2017-2018学年高二下学期期末考试数学(文)试题湖北省咸宁市2018-2019学年高二下学期期末数学(文)试题黑龙江省大庆实验中学2021届高三得分训练(二)数学(理)试题安徽省宣城市郎溪中学2020-2021学年高二下学期第一次月考理科数学试题四川省仁寿第一中学校北校区2020-2021学年高二6月期末数学(文)试题广西河池市九校2020-2021学年高二下学期第二次联考数学(理)试题(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)数学(上海B卷)河南省灵宝市第五高级中学2021-2022学年高二下学期第一次月考数学文科试题
名校
10 . 已知定义在 上的函数
上的函数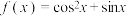 .
.
(1)求 的极大值点;
的极大值点;
(2)证明:对任意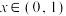 ,
,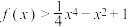 .
.
 上的函数
上的函数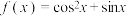 .
.(1)求
 的极大值点;
的极大值点;(2)证明:对任意
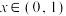 ,
,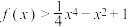 .
.
您最近一年使用:0次



