名校
1 . 已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)当 时,直线
时,直线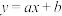 是曲线
是曲线 的切线,求
的切线,求 的最小值;
的最小值;
(3)若方程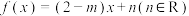 有两个实数根.
有两个实数根.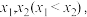 证明:
证明: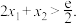
 .
.(1)讨论函数
 的单调性;
的单调性;(2)当
 时,直线
时,直线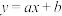 是曲线
是曲线 的切线,求
的切线,求 的最小值;
的最小值;(3)若方程
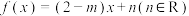 有两个实数根.
有两个实数根.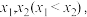 证明:
证明: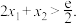
您最近一年使用:0次
2 . 已知函数 ,(
,( 为自然对数的底数).
为自然对数的底数).
(1)求函数 的单调区间:
的单调区间:
(2)设 在
在 处的切线方程为
处的切线方程为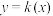 ,求证:当
,求证:当 时,
时,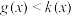 ;
;
(3)若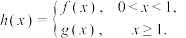 ,存在
,存在 ,使得
,使得 ,且
,且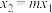 ,求证:当
,求证:当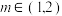 时,
时, .
.
 ,(
,( 为自然对数的底数).
为自然对数的底数).(1)求函数
 的单调区间:
的单调区间:(2)设
 在
在 处的切线方程为
处的切线方程为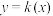 ,求证:当
,求证:当 时,
时,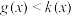 ;
;(3)若
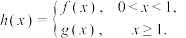 ,存在
,存在 ,使得
,使得 ,且
,且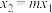 ,求证:当
,求证:当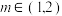 时,
时, .
.
您最近一年使用:0次
名校
3 . 已知函数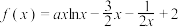 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 时,
时, ,求a的取值范围;
,求a的取值范围;
(3)对于任意 ,证明:
,证明: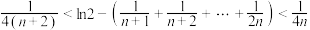 .
.
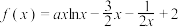 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若
 时,
时, ,求a的取值范围;
,求a的取值范围;(3)对于任意
 ,证明:
,证明: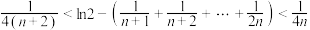 .
.
您最近一年使用:0次
2024-01-18更新
|
2380次组卷
|
10卷引用:天津市和平区耀华中学2024届高三下学期寒假验收考数学试卷
天津市和平区耀华中学2024届高三下学期寒假验收考数学试卷山东省济南市2024届高三上学期期末学习质量检测数学试题广东省佛山市第一中学2024届高三下学期开学预测数学试题(一)辽宁省沈阳市、大连市2023-2024学年高二上学期教学联盟大联考数学试题(已下线)5.3.1函数的单调性 第三练 能力提升拔高四川省成都市第七中学2024届高三上学期期末数学(理)试题(已下线)信息必刷卷04(天津专用)河南省濮阳市第一高级中学2023-2024学年高二下学期5月期中质量检测数学试题上海市华东师范大学第二附属中学2023-2024学年高二下学期5月月考数学试题四川省眉山市彭山区第一中学2024-2025学年高三上学期10月月考数学试卷
名校
4 . 已知函数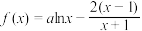
(1)当 时,求
时,求 在点
在点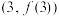 处的切线方程;
处的切线方程;
(2)若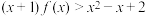 对
对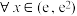 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(3) 若有3个零点
若有3个零点 ,其中
,其中 ,求实数
,求实数 的取值范围,并证明
的取值范围,并证明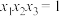 .
.
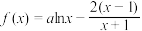
(1)当
 时,求
时,求 在点
在点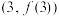 处的切线方程;
处的切线方程;(2)若
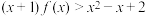 对
对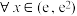 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围(3)
 若有3个零点
若有3个零点 ,其中
,其中 ,求实数
,求实数 的取值范围,并证明
的取值范围,并证明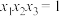 .
.
您最近一年使用:0次
2023-11-30更新
|
935次组卷
|
3卷引用:天津市和平区天津一中2024届高三上学期第三次月考数学试题
名校
5 . 已知函数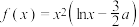 ,a为实数.
,a为实数.
(1)当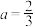 时,求函数在
时,求函数在 处的切线方程;
处的切线方程;
(2)求函数 的单调区间;
的单调区间;
(3)若函数 在
在 处取得极值,
处取得极值, 是函数
是函数 的导函数,且
的导函数,且 ,
, ,证明:
,证明: .
.
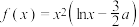 ,a为实数.
,a为实数.(1)当
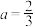 时,求函数在
时,求函数在 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3)若函数
 在
在 处取得极值,
处取得极值, 是函数
是函数 的导函数,且
的导函数,且 ,
, ,证明:
,证明: .
.
您最近一年使用:0次
名校
解题方法
6 . 设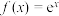 ,
,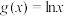 ,
,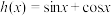 .
.
(1)求函数 ,
, 的单调区间和极值;
的单调区间和极值;
(2)若关于x不等式 在区间
在区间 上恒成立,求实数a的值;
上恒成立,求实数a的值;
(3)若存在直线 ,其与曲线
,其与曲线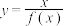 和
和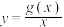 共有3个不同交点
共有3个不同交点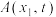 ,
, ,
,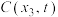 (
( ),求证:
),求证: 成等比数列.
成等比数列.
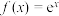 ,
,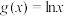 ,
,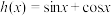 .
.(1)求函数
 ,
, 的单调区间和极值;
的单调区间和极值;(2)若关于x不等式
 在区间
在区间 上恒成立,求实数a的值;
上恒成立,求实数a的值;(3)若存在直线
 ,其与曲线
,其与曲线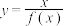 和
和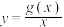 共有3个不同交点
共有3个不同交点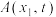 ,
, ,
,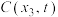 (
( ),求证:
),求证: 成等比数列.
成等比数列.
您最近一年使用:0次
7 . 已知函数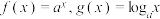 ,其中
,其中 ,
,
(1)若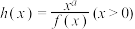 ,
,
(i)当 时,求
时,求 的单调区间;
的单调区间;
(ii)曲线 与直线
与直线 有且仅有两个交点,求
有且仅有两个交点,求 的取值范围.
的取值范围.
(2)证明:当 时,存在直线
时,存在直线 ,使直线
,使直线 是曲线
是曲线 的切线,也是曲线
的切线,也是曲线 的切线.
的切线.
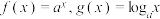 ,其中
,其中 ,
,(1)若
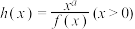 ,
,(i)当
 时,求
时,求 的单调区间;
的单调区间;(ii)曲线
 与直线
与直线 有且仅有两个交点,求
有且仅有两个交点,求 的取值范围.
的取值范围.(2)证明:当
 时,存在直线
时,存在直线 ,使直线
,使直线 是曲线
是曲线 的切线,也是曲线
的切线,也是曲线 的切线.
的切线.
您最近一年使用:0次
2023-04-26更新
|
1084次组卷
|
3卷引用:天津市和平区2023届高三二模数学试题
名校
解题方法
8 . 已知函数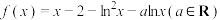 .
.
(1)令 ,讨论
,讨论 的单调性并求极值;
的单调性并求极值;
(2)令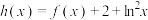 ,若
,若 有两个零点;
有两个零点;
(i)求a的取值范围:
(ii)若方程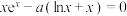 有两个实根
有两个实根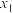 ,
,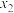 ,
, ,证明:
,证明: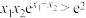 .
.
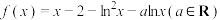 .
.(1)令
 ,讨论
,讨论 的单调性并求极值;
的单调性并求极值;(2)令
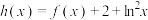 ,若
,若 有两个零点;
有两个零点;(i)求a的取值范围:
(ii)若方程
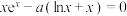 有两个实根
有两个实根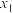 ,
,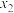 ,
, ,证明:
,证明: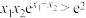 .
.
您最近一年使用:0次
2022-10-26更新
|
2388次组卷
|
10卷引用:天津市第二南开学校2021-2022学年高三上学期期中数学试题
天津市第二南开学校2021-2022学年高三上学期期中数学试题天津市耀华中学2022届高三下学期统练9数学试题天津市滨海七校2020-2021学年高三上学期期末联考数学试题四川省绵阳南山中学2022-2023学年高三上学期绵阳一诊热身考试理科数学试题黑龙江省哈尔滨市第九中学校2022-2023学年高三上学期第三次月考数学试题天津市北京师范大学天津附属中学2022-2023学年高三上学期期末数学试题(已下线)第二篇 函数与导数 专题6 函数周期性、对称性、拐点 微点2 函数的拐点与对称中心天津市实验中学滨海学校2022-2023学年高二下学期期中数学试题(已下线)模块八 专题11 以函数与导数为背景的压轴解答题(已下线)北京市丰台区2023届高三下学期3月一模数学试题变式题16-21
名校
9 . 已知函数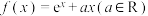 ,
,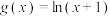 .
.
(1)当 时,求函数
时,求函数 在点
在点 处的切线;
处的切线;
(2)若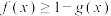 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证: 时,
时,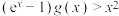 .
.
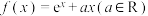 ,
,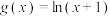 .
.(1)当
 时,求函数
时,求函数 在点
在点 处的切线;
处的切线;(2)若
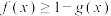 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)求证:
 时,
时,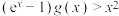 .
.
您最近一年使用:0次
2022-05-29更新
|
1553次组卷
|
5卷引用:天津市耀华中学2022届高三下学期一模数学试题
名校
10 . 已知 ,设函数
,设函数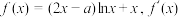 是
是 的导函数.
的导函数.
(1)若 ,求曲线
,求曲线 在点
在点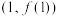 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上存在两个不同的零点
上存在两个不同的零点 ,
,
①求实数a范围;
②证明: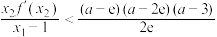 .
.
注,其中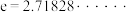 是自然对数的底数.
是自然对数的底数.
 ,设函数
,设函数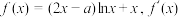 是
是 的导函数.
的导函数.(1)若
 ,求曲线
,求曲线 在点
在点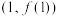 处的切线方程;
处的切线方程;(2)若
 在区间
在区间 上存在两个不同的零点
上存在两个不同的零点 ,
,①求实数a范围;
②证明:
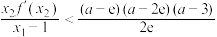 .
.注,其中
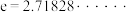 是自然对数的底数.
是自然对数的底数.
您最近一年使用:0次
2022-05-13更新
|
949次组卷
|
3卷引用:天津市第一中学2022-2023学年高三上学期第一次月考数学试题



