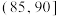2023·全国·模拟预测
解题方法
1 . 玻璃缸中装有2个黑球和4个白球,现从中先后无放回地取2个球.记“第一次取得黑球”为 ,“第一次取得白球”为
,“第一次取得白球”为 ,“第二次取得黑球”为
,“第二次取得黑球”为 ,“第二次取得白球”为
,“第二次取得白球”为 ,则( )
,则( )
 ,“第一次取得白球”为
,“第一次取得白球”为 ,“第二次取得黑球”为
,“第二次取得黑球”为 ,“第二次取得白球”为
,“第二次取得白球”为 ,则( )
,则( )A. | B. |
C. | D.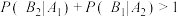 |
您最近半年使用:0次
名校
2 . 甲、乙两人进行知识问答比赛,共有 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
(1)若 ,
, ,求甲获胜的概率;
,求甲获胜的概率;
(2)若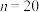 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:
①设随机变量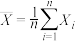 ,若以观测值
,若以观测值 的均值
的均值 作为
作为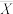 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值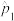 ;
;
②设随机变量 取到观测值
取到观测值 的概率为
的概率为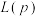 ,即
,即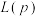
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得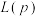 达到最大时
达到最大时 的取值
的取值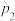 作为参数
作为参数 的一个估计值.求
的一个估计值.求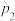 .
.
表1:甲得分的一组观测值.
附:若随机变量 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则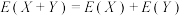 .
.
 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.(1)若
 ,
, ,求甲获胜的概率;
,求甲获胜的概率;(2)若
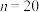 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:①设随机变量
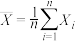 ,若以观测值
,若以观测值 的均值
的均值 作为
作为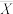 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值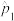 ;
;②设随机变量
 取到观测值
取到观测值 的概率为
的概率为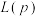 ,即
,即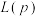
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得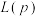 达到最大时
达到最大时 的取值
的取值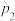 作为参数
作为参数 的一个估计值.求
的一个估计值.求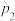 .
.| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分 | 1 | 0 | 0 | ﹣1 | 1 | 1 | ﹣1 | 0 | 0 | 0 |
| 题目 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 得分 | ﹣1 | 0 | 1 | 1 | ﹣1 | 0 | 0 | 0 | 1 | 0 |
附:若随机变量
 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则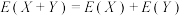 .
.
您最近半年使用:0次
今日更新
|
614次组卷
|
2卷引用:浙江省天域全国名校协作体2023-2024学年高三二模数学试题
解题方法
3 . 若随机变量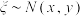 ,且
,且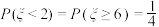 ,则( )
,则( )
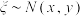 ,且
,且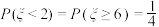 ,则( )
,则( )A.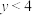 | B. | C. | D. |
您最近半年使用:0次
4 . 张先生每周有5个工作日,工作日出行采用自驾方式,必经之路上有一个十字路口,直行车道有三条,直行车辆可以随机选择一条车道通行,记事件 为“张先生驾车从左侧直行车道通行”.
为“张先生驾车从左侧直行车道通行”.
(1)某日张先生驾车上班接近路口时,看到自己车前是一辆大货车,遂选择不与大货车从同一车道通行.记事件 为“大货车从中间直行车道通行”,求
为“大货车从中间直行车道通行”,求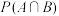 ;
;
(2)用 表示张先生每周工作日出行事件
表示张先生每周工作日出行事件 发生的次数,求
发生的次数,求 的分布及期望
的分布及期望 .
.
 为“张先生驾车从左侧直行车道通行”.
为“张先生驾车从左侧直行车道通行”.(1)某日张先生驾车上班接近路口时,看到自己车前是一辆大货车,遂选择不与大货车从同一车道通行.记事件
 为“大货车从中间直行车道通行”,求
为“大货车从中间直行车道通行”,求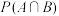 ;
;(2)用
 表示张先生每周工作日出行事件
表示张先生每周工作日出行事件 发生的次数,求
发生的次数,求 的分布及期望
的分布及期望 .
.
您最近半年使用:0次
解题方法
5 . 已知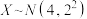 ,若
,若 ,则
,则
______ .
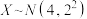 ,若
,若 ,则
,则
您最近半年使用:0次
名校
解题方法
6 . 设某批产品中,甲、乙、丙三个车间生产的产品分别为50%,30%,20%,甲、乙车间生产的产品的次品率分别为3%,5%,现从中任取一件,若取到的是次品的概率为3.6%,则推测丙车间的次品率为( )
| A.2% | B.3% | C.4% | D.5% |
您最近半年使用:0次
解题方法
7 . 据统计,2024年元旦假期,哈尔滨市累计接待游客304.79万人次,实现旅游总收入59.14亿元,游客接待量与旅游总收入达到历史峰值.现对某一时间段冰雪大世界的部分游客做问卷调查,其中75%的游客计划只游览冰雪大世界,另外25%的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.
(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为X,求X的分布列及数学期望;
(2)记 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 .
.
(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为X,求X的分布列及数学期望;
(2)记
 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 .
.
您最近半年使用:0次
解题方法
8 . 赣南脐橙,果大形正,橙红鲜绝,光洁美观,已被列为全国十一大优势农产品之一,是江西省赣州市特产,中国国家地理标志产品.荣获“中华名果”等称号.有甲、乙两个脐橙种植基地,按果径 (单位:
(单位: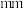 )的大小分级,其中
)的大小分级,其中 为特级果,
为特级果,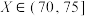 为一级果,
为一级果,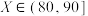 为二级果,
为二级果, 为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
(1)根据以上统计数据完成下表,并回答是否有 以上的把握认为“脐橙果径与所在基地有关?”
以上的把握认为“脐橙果径与所在基地有关?”
(2)以样本估计总体,用频率代替概率,从甲种植基地采摘的所有优质果中随机抽取3个,设被抽取的3个脐橙中特级果的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附: ,
, .
.
 (单位:
(单位: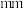 )的大小分级,其中
)的大小分级,其中 为特级果,
为特级果,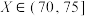 为一级果,
为一级果,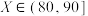 为二级果,
为二级果, 为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:果径分组(单位: |
|
|
|
|
|
|
甲基地频数 | 5 | 15 | 100 | 150 | 25 | 5 |
乙基地频数 | 10 | 25 | 110 | 120 | 25 | 10 |
 以上的把握认为“脐橙果径与所在基地有关?”
以上的把握认为“脐橙果径与所在基地有关?”甲基地 | 乙基地 | |
优质果 | ||
非优质果 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 ,
, .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
名校
9 . 掷两次质地均匀的骰子
(1)若其中有一次点数是偶数,则在此情况下另一次也是偶数的概率.
(2)设事件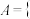 第一次的点数为4
第一次的点数为4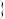 ,事件
,事件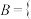 两次点数和为6
两次点数和为6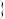 ,事件
,事件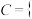 两次点数和为7
两次点数和为7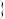 ,判断事件
,判断事件 和事件
和事件 是否独立,事件
是否独立,事件 和事件
和事件 是否独立?
是否独立?
(1)若其中有一次点数是偶数,则在此情况下另一次也是偶数的概率.
(2)设事件
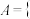 第一次的点数为4
第一次的点数为4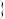 ,事件
,事件 两次点数和为6
两次点数和为6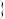 ,事件
,事件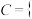 两次点数和为7
两次点数和为7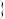 ,判断事件
,判断事件 和事件
和事件 是否独立,事件
是否独立,事件 和事件
和事件 是否独立?
是否独立?
您最近半年使用:0次
名校
解题方法
10 . 10件产品中有8件合格,2件次品,一次取两件产品,其中有次品的概率是______ .
您最近半年使用:0次