解题方法
1 . 已知二次函数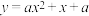 的值域为
的值域为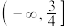 ,则实数
,则实数
________ .
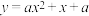 的值域为
的值域为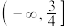 ,则实数
,则实数
您最近一年使用:0次
名校
解题方法
2 . 二次函数 在
在 上最大值为1,则实数a值为( )
上最大值为1,则实数a值为( )
 在
在 上最大值为1,则实数a值为( )
上最大值为1,则实数a值为( )A. | B. |
C. 或 或 | D. 或 或 |
您最近一年使用:0次
名校
解题方法
3 . 已知函数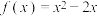 ,
, ,若
,若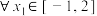 ,
,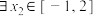 ,使得
,使得 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
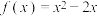 ,
, ,若
,若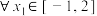 ,
,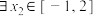 ,使得
,使得 ,则实数a的取值范围是( )
,则实数a的取值范围是( )A.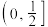 | B. | C.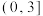 | D.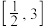 |
您最近一年使用:0次
2024-07-12更新
|
661次组卷
|
2卷引用:北京市首都师范大学附属中学2023-2024学年高二下学期6月月考数学试题
解题方法
4 . 已知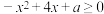 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是
的取值范围是________ .
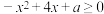 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
名校
解题方法
5 . 已知函数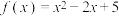 在
在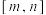 上的值域为
上的值域为 ,则
,则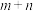 的值为
的值为______ .
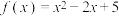 在
在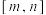 上的值域为
上的值域为 ,则
,则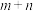 的值为
的值为
您最近一年使用:0次
2024-07-07更新
|
508次组卷
|
2卷引用:辽宁省部分学校2023-2024学年高二下学期6月份阶段考试数学试卷
名校
解题方法
6 . 已知函数 .
.
(1)若 ,求不等式
,求不等式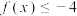 的解集;
的解集;
(2)若 时,
时, 的最小值为
的最小值为 ,求
,求 的值.
的值.
 .
.(1)若
 ,求不等式
,求不等式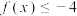 的解集;
的解集;(2)若
 时,
时, 的最小值为
的最小值为 ,求
,求 的值.
的值.
您最近一年使用:0次
2024-06-13更新
|
492次组卷
|
2卷引用:四川省乐山市五通桥中学2023-2024学年高一上学期期中数学试题
名校
解题方法
7 . 若函数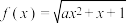 的值域为
的值域为 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
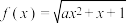 的值域为
的值域为 ,则实数
,则实数 的取值范围为( )
的取值范围为( )A.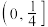 | B.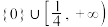 |
C. | D.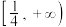 |
您最近一年使用:0次
2024-06-05更新
|
1088次组卷
|
5卷引用:云南曲靖市马龙区第一中学2023-2024学年高一上学期11月月考数学试卷
名校
解题方法
8 . 设 ,函数
,函数 的定义域为
的定义域为 .若对满足
.若对满足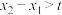 的任意
的任意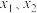 ,均有
,均有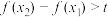 ,则称函数
,则称函数 具有“
具有“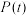 性质”.
性质”.
(1)在下述条件下,分别判断函数 是否具有
是否具有 性质,并说明理由;
性质,并说明理由;
①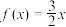 ; ②
; ②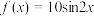 ;
;
(2)已知 ,且函数
,且函数 具有
具有 性质,求实数
性质,求实数 的取值范围;
的取值范围;
(3)证明:“函数 为增函数”是“对任意
为增函数”是“对任意 ,函数
,函数 均具有
均具有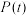 性质”的充要条件.
性质”的充要条件.
 ,函数
,函数 的定义域为
的定义域为 .若对满足
.若对满足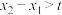 的任意
的任意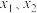 ,均有
,均有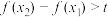 ,则称函数
,则称函数 具有“
具有“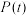 性质”.
性质”.(1)在下述条件下,分别判断函数
 是否具有
是否具有 性质,并说明理由;
性质,并说明理由;①
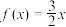 ; ②
; ②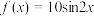 ;
;(2)已知
 ,且函数
,且函数 具有
具有 性质,求实数
性质,求实数 的取值范围;
的取值范围;(3)证明:“函数
 为增函数”是“对任意
为增函数”是“对任意 ,函数
,函数 均具有
均具有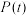 性质”的充要条件.
性质”的充要条件.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
9 . 已知函数 的值域为
的值域为 ,则实数
,则实数 的值为
的值为______ .
 的值域为
的值域为 ,则实数
,则实数 的值为
的值为
您最近一年使用:0次
解题方法
10 . 已知函数 ,设
,设 ,
,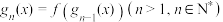 .且关于
.且关于 的函数
的函数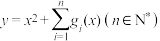 .则( )
.则( )
 ,设
,设 ,
,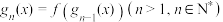 .且关于
.且关于 的函数
的函数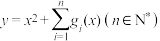 .则( )
.则( )A. 或 或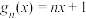 |
B.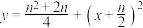 |
C.当 时,存在关于 时,存在关于 的函数 的函数 在区间 在区间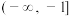 上的最小值为6, 上的最小值为6, |
D.当 时,存在关于 时,存在关于 的函数 的函数 在区间 在区间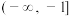 上的最小值为6, 上的最小值为6, |
您最近一年使用:0次



