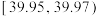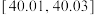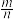名校
解题方法
1 . 在刚刚过去的寒假,由于新冠疫情的影响,哈尔滨市的 、
、 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取
两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取 名学生,对每名学生进行综合测试评分,记综合评分为
名学生,对每名学生进行综合测试评分,记综合评分为 及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有
及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有 名优秀学生,且
名优秀学生,且 学校的优秀学生占该校抽取总人数的
学校的优秀学生占该校抽取总人数的 .
.
(1)填写下面的列联表,并判断能否在犯错误概率不超过 的前提下认为学生综合测试评分优秀与教学方案有关.
的前提下认为学生综合测试评分优秀与教学方案有关.
(2)在 学校的
学校的 名学生中依据综合测评是否优秀进行分层抽样,抽取容量为
名学生中依据综合测评是否优秀进行分层抽样,抽取容量为 的样本,在
的样本,在 名学生中随机抽取
名学生中随机抽取 名同学,求
名同学,求 名同学都是优秀学生的概率.
名同学都是优秀学生的概率.
附:
 ,其中
,其中 .
.
 、
、 两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取
两所同类学校的高三学年分别采用甲、乙两种方案进行线上教学,为观测其教学效果,分别在两所学校的高三学年各随机抽取 名学生,对每名学生进行综合测试评分,记综合评分为
名学生,对每名学生进行综合测试评分,记综合评分为 及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有
及以上的学生为优秀学生.经统计得到两所学校抽取的学生中共有 名优秀学生,且
名优秀学生,且 学校的优秀学生占该校抽取总人数的
学校的优秀学生占该校抽取总人数的 .
.(1)填写下面的列联表,并判断能否在犯错误概率不超过
 的前提下认为学生综合测试评分优秀与教学方案有关.
的前提下认为学生综合测试评分优秀与教学方案有关.(2)在
 学校的
学校的 名学生中依据综合测评是否优秀进行分层抽样,抽取容量为
名学生中依据综合测评是否优秀进行分层抽样,抽取容量为 的样本,在
的样本,在 名学生中随机抽取
名学生中随机抽取 名同学,求
名同学,求 名同学都是优秀学生的概率.
名同学都是优秀学生的概率.| 优秀学生 | 非优秀学生 | 合计 | |
| 甲方案 | |||
| 乙方案 | |||
| 合计 |
 | 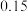 |  |  |  |  |  |  |
 | 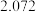 |  |  |  |  |  |  |
 ,其中
,其中 .
.
您最近半年使用:0次
2021-05-05更新
|
665次组卷
|
4卷引用:黑龙江省哈尔滨市第三中学2021届高三第三次模拟考试数学(文科)试题
黑龙江省哈尔滨市第三中学2021届高三第三次模拟考试数学(文科)试题(已下线)文科数学-2021年高考考前20天终极冲刺攻略+(三)(6月1日)全国Ⅱ卷决胜高考2021届高三数学(理)仿真卷试题(七)黑龙江省哈尔滨市第三中学校2021届高三三模数学(文)试题
19-20高三下·全国·阶段练习
解题方法
2 . 在机械化生产车间里,工人们在排列整齐的工作台旁紧张地生产同一种产品,工作台上方一条传送带在运转,带上设置若干钩子,钩子均匀排列,如图,工人将产品挂在经过他上方的钩子上带走.当生产进入稳定状态后,每个工人生产一件产品所需时间是不变的,而他挂产品的时刻是随机的.每个工人在任何时刻都能触到一只钩子,且只能触到一只,在他生产出一件产品的瞬间,如果他能触到的钩子是空的,则可将产品挂上带走;如果非空,则他只能将产品放下.放下的产品就永远退出这个传送系统.衡量这种传送系统的效率可以看它能否及时把工人的产品带走.显然,在工人数目不变的情况下传送带速度越快,带上钩子数越多,效率越高.设在一个周期内有m个钩子通过每一工作台上方,且到达第一个工作台上方的钩子都是空的.可将传送系统的效率D 定义为一个周期内(每个工人只生产一件产品)带走的产品数s与生产的全部产品数n之比,且满足关系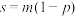 ,p为一个周期内每只钩子为空钩的概率.
,p为一个周期内每只钩子为空钩的概率.
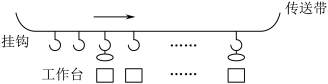
(1)当m=3,n=4时,求D的值;
(2)若m远大于n,试研究提高传送带效率的途径.
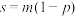 ,p为一个周期内每只钩子为空钩的概率.
,p为一个周期内每只钩子为空钩的概率.
(1)当m=3,n=4时,求D的值;
(2)若m远大于n,试研究提高传送带效率的途径.
您最近半年使用:0次
解题方法
3 . 已知某校甲、乙、丙三个兴趣小组的学生人数分别为36,24,12.现采用分层抽样的方法从中抽取6人,进行睡眠质量的调查.
(Ⅰ)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?
(Ⅱ)现从6人中随机抽取2人做进一步的身体检查,求抽取的2人来自同一兴趣小组的概率.
(Ⅰ)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?
(Ⅱ)现从6人中随机抽取2人做进一步的身体检查,求抽取的2人来自同一兴趣小组的概率.
您最近半年使用:0次
2020-09-04更新
|
433次组卷
|
3卷引用:陕西省西安市蓝田县2019-2020学年高一下学期期末数学试题
陕西省西安市蓝田县2019-2020学年高一下学期期末数学试题(已下线)10.2 事件的相互独立性 2020-2021高中数学新教材配套提升训练(人教A版必修第二册)陕西省榆林市府谷县第三中学2020-2021学年高二上学期期中文科数学试题
19-20高一·全国·课后作业
4 . 某校按分层随机抽样的方法从高中三个年级抽取部分学生调查,从三个年级抽取人数的比例为如图所示的扇形面积比,已知高二年级共有学生1 200人,并从中抽取了40人.

(1)该校的总人数为多少?
(2)三个年级分别抽取多少人?

(1)该校的总人数为多少?
(2)三个年级分别抽取多少人?
您最近半年使用:0次
名校
5 . 某几位大学生自主创业创办了一个服务公司提供 、
、 两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买
两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买 的概率为
的概率为 、购买
、购买 的概率为
的概率为 ,而前一次购买
,而前一次购买 产品的人下一次来购买
产品的人下一次来购买 产品的概率为
产品的概率为 、购买
、购买 产品的概率为
产品的概率为 ,前一次购买
,前一次购买 产品的人下一次来购买
产品的人下一次来购买 产品的概率为
产品的概率为 、购买
、购买 产品的概率也是
产品的概率也是 ,如此往复.记某人第
,如此往复.记某人第 次来购买
次来购买 产品的概率为
产品的概率为 .
.
(1)求 ,并证明数列
,并证明数列 是等比数列;
是等比数列;
(2)记第二次来公司购买产品的3个人中有 个人购买
个人购买 产品,求
产品,求 的分布列并求
的分布列并求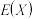 ;
;
(3)经过一段时间的经营每天来购买产品的人稳定在800人,假定这800人都已购买过很多次该两款产品,那么公司每天应至少准备 、
、 产品各多少份.(直接写结论、不必说明理由).
产品各多少份.(直接写结论、不必说明理由).
 、
、 两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买
两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买 的概率为
的概率为 、购买
、购买 的概率为
的概率为 ,而前一次购买
,而前一次购买 产品的人下一次来购买
产品的人下一次来购买 产品的概率为
产品的概率为 、购买
、购买 产品的概率为
产品的概率为 ,前一次购买
,前一次购买 产品的人下一次来购买
产品的人下一次来购买 产品的概率为
产品的概率为 、购买
、购买 产品的概率也是
产品的概率也是 ,如此往复.记某人第
,如此往复.记某人第 次来购买
次来购买 产品的概率为
产品的概率为 .
.(1)求
 ,并证明数列
,并证明数列 是等比数列;
是等比数列;(2)记第二次来公司购买产品的3个人中有
 个人购买
个人购买 产品,求
产品,求 的分布列并求
的分布列并求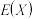 ;
;(3)经过一段时间的经营每天来购买产品的人稳定在800人,假定这800人都已购买过很多次该两款产品,那么公司每天应至少准备
 、
、 产品各多少份.(直接写结论、不必说明理由).
产品各多少份.(直接写结论、不必说明理由).
您最近半年使用:0次
2020-08-07更新
|
2362次组卷
|
3卷引用:湖北省武汉市2020届高三下学期六月供题(二)数学(理)试题
解题方法
6 . 某中学从甲、乙两个班中各选出7名学生参加数学竞赛,将他们的成绩(满分100分)进行统计分析,绘制成如图所示的茎叶图.已知甲班学生成绩的众数是83,乙班学生成绩的平均数是86.

(1)求x,y的值;
(2)设成绩在85分以上(含85分)的学生为优秀学生.从甲、乙两班的优秀学生中各取1人,记甲班选取的学生成绩不低于乙班选取的学生成绩为事件A,求事件A发生的概率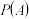 .
.

(1)求x,y的值;
(2)设成绩在85分以上(含85分)的学生为优秀学生.从甲、乙两班的优秀学生中各取1人,记甲班选取的学生成绩不低于乙班选取的学生成绩为事件A,求事件A发生的概率
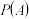 .
.
您最近半年使用:0次
7 . 某高校的入学面试中有4道不同的题目,每位面试者都要回答这4道题目.已知李明答对第1题、第2题、第3题、第4题的概率分别为 假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).
假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).
(1)写出所有的样本点;
(2)求李明通过面试的概率.
 假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).
假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).(1)写出所有的样本点;
(2)求李明通过面试的概率.
您最近半年使用:0次
2020-07-27更新
|
763次组卷
|
5卷引用:山东省枣庄市2019-2020学年高一(下)期末数学试题
山东省枣庄市2019-2020学年高一(下)期末数学试题(已下线)4.1.2、4.1.3 乘法公式与全概率公式、独立性与条件概率的关系-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)(已下线)专题10.2事件的相互独立性+单元测试(A卷基础篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)10.2事件的相互独立性(精练)-2020-2021学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)专题4.1 条件概率与事件的独立性(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)
解题方法
8 . “绿水青山就是金山银山”,为了响应国家政策,我市环保部门对市民进行了一次环境保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的50人的得分(满分:100分)数据,统计结果如表所示:
若规定问卷得分不低于70分的市民称为“环境保护关注者”,则上图中表格可得 列联表如下:
列联表如下:
(1)请完成上述 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环境保护达人”,现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答,再从这4名市民中随机抽取2人参与座谈会,求抽取的2名市民中,既有男“环境保护达人”又有女“环境保护达人”的概率.
附表及公式: ,其中
,其中 .
.
| 组别 |  | 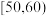 | 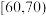 |  |  | 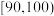 |
| 男 | 1 | 2 | 2 | 10 | 9 | 6 |
| 女 | 0 | 5 | 5 | 5 | 3 | 2 |
若规定问卷得分不低于70分的市民称为“环境保护关注者”,则上图中表格可得
 列联表如下:
列联表如下:| 非“环境保护关注者” | 是“环境保护关注者” | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
(1)请完成上述
 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?(2)若问卷得分不低于80分的人称为“环境保护达人”,现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答,再从这4名市民中随机抽取2人参与座谈会,求抽取的2名市民中,既有男“环境保护达人”又有女“环境保护达人”的概率.
附表及公式:
 ,其中
,其中 .
.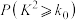 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
9 . 某制造商2019年8月份生产了一批乒乓球,随机抽取100个进行检查,测得每个乒乓球的直径(单位:mm),将数据分组如下表:
(1)请将上表补充完整;
(2)已知标准乒乓球的直径为 ,试估计这批乒乓球的直径误差不超过
,试估计这批乒乓球的直径误差不超过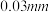 的概率.
的概率.
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |
(2)已知标准乒乓球的直径为
 ,试估计这批乒乓球的直径误差不超过
,试估计这批乒乓球的直径误差不超过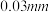 的概率.
的概率.
您最近半年使用:0次
10 . 为了解某种产品的质量,从一大批产品中抽出若干批进行质量检查,结果如下:
(1)计算各批产品中优等品的频率,把上表补充完整;
(2)从这一大批产品中随机抽取1个,则抽到优等品的概率约是多少?
抽取个数 | 50 | 100 | 200 | 500 | 1000 | 2000 |
优等品数 | 45 | 92 | 194 | 470 | 954 | 1902 |
优等品频率 |
(2)从这一大批产品中随机抽取1个,则抽到优等品的概率约是多少?
您最近半年使用:0次