解题方法
1 . 已知函数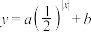 的图象过原点,且无限接近直线
的图象过原点,且无限接近直线 但又不与该直线相交,则该函数的解析式为
但又不与该直线相交,则该函数的解析式为______ ,单调递增区间为______ .
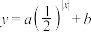 的图象过原点,且无限接近直线
的图象过原点,且无限接近直线 但又不与该直线相交,则该函数的解析式为
但又不与该直线相交,则该函数的解析式为
您最近一年使用:0次
2 . 已知函数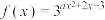 .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)若 的最大值为9,求a的值.
的最大值为9,求a的值.
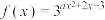 .
.(1)当
 时,求
时,求 的值域;
的值域;(2)若
 的最大值为9,求a的值.
的最大值为9,求a的值.
您最近一年使用:0次
2023-11-28更新
|
816次组卷
|
4卷引用:山东省泰安市肥城市第一高级中学2023-2024学年高一上学期12月月考数学试题
山东省泰安市肥城市第一高级中学2023-2024学年高一上学期12月月考数学试题河南省郑州市第四十四高级中学2023-2024学年高一上学期期中数学试题(已下线)专题04 与指数函数、对数函数有关的复合函数及函数方程综合应用-【寒假自学课】(人教A版2019)(已下线)4.2.2指数函数的图象和性质——课后作业(提升版)
名校
解题方法
3 . 已知函数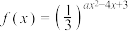 .
.
(1)若 ,求
,求 的单调区间
的单调区间
(2)若 有最大值3,求
有最大值3,求 的值
的值
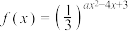 .
.(1)若
 ,求
,求 的单调区间
的单调区间(2)若
 有最大值3,求
有最大值3,求 的值
的值
您最近一年使用:0次
名校
解题方法
4 . 已知函数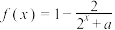 为定义在
为定义在 上的奇函数.
上的奇函数.
(1)求a的值;
(2)试判断函数的单调性,并用定义加以证明;
(3)若关于x的方程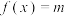 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
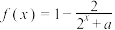 为定义在
为定义在 上的奇函数.
上的奇函数.(1)求a的值;
(2)试判断函数的单调性,并用定义加以证明;
(3)若关于x的方程
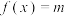 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 已知函数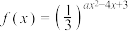 .
.
(1)若 ,求
,求 的单调区间
的单调区间
(2)若 有最大值3,求
有最大值3,求 的值
的值
(3)若 的值域是
的值域是 ,求
,求 的值
的值
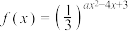 .
.(1)若
 ,求
,求 的单调区间
的单调区间(2)若
 有最大值3,求
有最大值3,求 的值
的值(3)若
 的值域是
的值域是 ,求
,求 的值
的值
您最近一年使用:0次
2023-04-10更新
|
2237次组卷
|
40卷引用:山东省泰安市肥城市慈明学校2025届高三上学期期中检测数学试题
山东省泰安市肥城市慈明学校2025届高三上学期期中检测数学试题2016-2017学年河北定兴三中高一上学期期中数学试卷西藏林芝市第一中学2018届高三9月月考数学(理)试题(已下线)2019高考备考一轮复习精品资料 【理】专题八 指数与指数函数 押题专练(已下线)2019高考备考一轮复习精品资料 【文】专题八 指数与指数函数 押题专练智能测评与辅导[文]-指数函数、对数函数、幂函数(已下线)专题2.6 指数与指数函数(讲)【文】-2020年高考一轮复习讲练测(已下线)专题2.6 指数与指数函数(讲)【理】-《2020年高考一轮复习讲练测》人教A版(2019) 必修第一册 突围者 第四章 易错疑难集训(一)山西省实验中学2017-2018学年高一上学期期中数学试题甘肃省兰州市第五十一中学2019-2020学年高一上学期期中数学试题(已下线)专题2.5 指数与指数函数(精测)-2021届高考数学(文)一轮复习讲练测(已下线)专题2.5 指数与指数函数(精讲)-2021届高考数学(文)一轮复习讲练测(已下线)专题2.5 指数与指数函数(精测)-2021届高考数学(理)一轮复习讲练测(已下线)考点09 指数函数(练习)-2021年高考数学复习一轮复习笔记(已下线)专题2.5 指数与指数函数-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破山西省晋中市祁县中学校2019-2020学年高二下学期6月月考数学(文)试题(已下线)专题2.5 指数与指数函数(精讲)-2021届高考数学(理)一轮复习讲练测陕西省商洛市商丹高新学校2018-2019学年高一上学期期末数学试题(已下线)【新东方】双师87(已下线)4.2 指数函数(精练)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教A版)(已下线)6.2.1 指数函数的概念、图象与性质(练习)-2020-2021学年上学期高一数学同步精品课堂(新教材苏教版必修第一册)青海省西宁市城西区青海湟川中学2020-2021学年高一上学期期末数学试题(已下线)第4课时 课后 指数函数的图象和性质的应用(已下线)专题09指数与指数函数-2022年(新高考)数学高频考点+重点题型(已下线)第07讲 指数与指数函数(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)2.4.6 指数函数(培优讲义)-2022年初升高数学无忧衔接安徽省马鞍山市第二中学2022-2023学年高一上学期期中数学试题第三章 指数运算与指数函数 单元测试-2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)第3课时 课后 指数函数的图象和性质的应用(完成)辽宁省大连市第八中学2021-2022学年高一上学期12月月考数学试题(已下线)考点10 指数函数 2024届高考数学考点总动员【练】(已下线)模块一 专题4 指数与指数函数(2)(人教A)(已下线)第三章 指数运算与指数函数章末测试-同步精品课堂(北师大版2019必修第一册)安徽省合肥市六校联盟2022-2023学年高一上学期期中联考数学试题山西省阳泉市郊区阳泉市第一中学校2023-2024学年高一上学期11月期中数学试题甘肃省武威市民勤县第一中学2023-2024学年高一上学期第二次月考数学试题(已下线)专题09 指数与指数函数(已下线)2.7指数函数(高三一轮)【讲】 (提升版)(已下线)专题拓展:指数型与对数型复合函数-【暑假自学课】-(人教A版2019必修第一册)
6 . 已知函数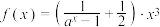 ,其中
,其中 且
且 .
.
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性;
的奇偶性;
(3)若关于 的不等式
的不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
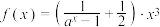 ,其中
,其中 且
且 .
.(1)求函数
 的定义域;
的定义域;(2)判断函数
 的奇偶性;
的奇偶性;(3)若关于
 的不等式
的不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-10更新
|
686次组卷
|
4卷引用:山东省淄博市2022-2023学年高一上学期期末数学试题
7 . 已知函数 的表达式为
的表达式为 .
.
(1)若 ,求函数
,求函数 的值域;
的值域;
(2)当 时,求函数
时,求函数 的最小值
的最小值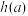 ;
;
(3)对于(2)中的函数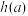 ,是否存在实数
,是否存在实数 ,同时满足下列两个条件:(i)
,同时满足下列两个条件:(i)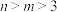 ;(ii)当
;(ii)当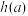 的定义域为
的定义域为 ,其值域为
,其值域为 ;若存在,求出
;若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的表达式为
的表达式为 .
.(1)若
 ,求函数
,求函数 的值域;
的值域;(2)当
 时,求函数
时,求函数 的最小值
的最小值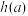 ;
;(3)对于(2)中的函数
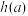 ,是否存在实数
,是否存在实数 ,同时满足下列两个条件:(i)
,同时满足下列两个条件:(i)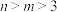 ;(ii)当
;(ii)当 的定义域为
的定义域为 ,其值域为
,其值域为 ;若存在,求出
;若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2022-12-02更新
|
1197次组卷
|
18卷引用:山东省滕州市第三中学2018届高三数学一轮复习专题:函数概念与基本初等函数
山东省滕州市第三中学2018届高三数学一轮复习专题:函数概念与基本初等函数河北省邯郸市大名一中2019-2020学年度高一上学期实验班10月月考数学试题(已下线)上海市华东师范大学第二附属中学2018-2019学年高一上学期期末数学试题2017年上海市长宁、嘉定区高三上学期期末质量调研(一模)数学试题2017年上海市嘉定区高考一模数学试题上海市上海交通大学附属中学2016-2017学年度高一上学期期末数学试题(已下线)6.1 幂函数-2020-2021学年高一数学课时同步练(苏教版2019必修第一册)(已下线)6.1 幂函数- 2021-2022学年高一数学10分钟课前预习练(苏教版2019)(已下线)专题6.3 幂函数、指数函数和对数函数 章末检测3(难)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(苏教版2019必修第一册)内蒙古霍林霍市一中2021-2022学年高一年级第一学期12月月考数学试题(已下线)专题05 二次函数(模拟练)上海交通大学附属中学2020-2021学年高一上学期12月月考数学试题上海市南洋模范中学2022-2023学年高一上学期12月月考数学试题上海师范大学附属中学2022-2023学年高一上学期期末数学试题(已下线)4.2 指数函数-同步精品课堂(沪教版2020必修第一册)(已下线)4.1 幂函数-同步精品课堂(沪教版2020必修第一册)上海市南汇中学2023-2024学年高一上学期12月月考数学试卷(已下线)第04讲 指数与指数函数(八大题型)(讲义)
名校
解题方法
8 . 若函数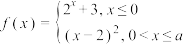 的定义域和值域的交集为空集,则正数
的定义域和值域的交集为空集,则正数 的取值范围是
的取值范围是______ .
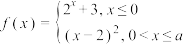 的定义域和值域的交集为空集,则正数
的定义域和值域的交集为空集,则正数 的取值范围是
的取值范围是
您最近一年使用:0次
2022-09-11更新
|
954次组卷
|
6卷引用:山东省济宁市嘉祥县第一中学2024-2025学年高三上学期10月月考数学试题
山东省济宁市嘉祥县第一中学2024-2025学年高三上学期10月月考数学试题北京市第五十七中学2023届高三上学期开学考试数学试题北京市第五十七中学2024届高三暑期检测(开学考试)数学试题(已下线)考点2 分段函数 2024届高考数学考点总动员 (讲)(已下线)函数及其表示03-一轮复习考点专练(已下线)考点08 分段函数 --高考数学100个黄金考点(2025届)【练】
名校
解题方法
9 . 已知函数 ,
,
(1)当 时,求函数
时,求函数 在
在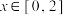 的值域
的值域
(2)若关于x的方程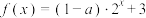 有解,求a的取值范围.
有解,求a的取值范围.
 ,
,
(1)当
 时,求函数
时,求函数 在
在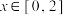 的值域
的值域(2)若关于x的方程
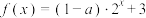 有解,求a的取值范围.
有解,求a的取值范围.
您最近一年使用:0次
2022-07-12更新
|
2253次组卷
|
11卷引用:山东省泰安市泰山中学2023-2024学年高一上学期期中数学试题
山东省泰安市泰山中学2023-2024学年高一上学期期中数学试题四川省雅安市2021-2022学年高二下学期期末数学(文)试题江苏省扬州市宝应县2022-2023学年高三上学期期初检测数学试题安徽省安庆市怀宁县第二中学2022-2023学年高三上学期第一次月考数学试题(已下线)专题04 幂函数、指数函数与对数函数(讲义)-2(已下线)突破4.2 指数函数(课时训练)-【新教材优创】突破满分数学之2022-2023学年高一数学重难点突破+课时训练 (人教A版2019必修第一册)(已下线)期末模拟卷02(测试范围:必修第一册全部内容)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)新疆乌鲁木齐市新疆实验中学2022-2023学年高一上学期期中考试数学试题上海市进才中学2023-2024学年高一上学期期中数学试题单元测试B卷——第四章 指数函数与对数函数江苏省宿迁市泗阳县王集中学2024-2025学年高三上学期第一次质量调研数学试卷(艺术班)
10-11高一·广东河源·期中
10 . 若直线 与函数
与函数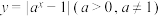 的图象有两个公共点,则a的取值范围是
的图象有两个公共点,则a的取值范围是______ .
 与函数
与函数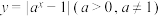 的图象有两个公共点,则a的取值范围是
的图象有两个公共点,则a的取值范围是
您最近一年使用:0次
2021-12-02更新
|
2288次组卷
|
41卷引用:山东省青岛市青岛第五十八中学2021-2022学年高一上学期期中数学试题
山东省青岛市青岛第五十八中学2021-2022学年高一上学期期中数学试题(已下线)2010-2011年广东省龙川一中高一期中考试数学试卷(已下线)2011-2012学年浙江省温州市直六校高一上学期期中数学试卷(已下线)2011-2012学年浙江省衢州一中高二下学期期中文科数学试卷北京市朝阳陈经纶中学2016-2017学年高一上期中数学试题【全国百强校】贵州省铜仁市第一中学2018-2019学年高一上学期期中数学试题安徽省滁州市民办高中2018-2019学年高一上学期第三次月考数学试题江西省赣州市于都二中2019-2020学年高一上学期第二次月考数学试题新疆博尔塔拉蒙古自治州第五师高级中学2019-2020学年高一上学期第二次月考数学试卷(已下线)专题2.5 指数与指数函数(精测)-2021届高考数学(文)一轮复习讲练测(已下线)[新教材精创] 3.3.2 指数函数的图象和性质(2)练习(1) -北师大版高中数学必修第一册内蒙古乌兰察布市集宁一中西校区2019-2020学年高二(下)期末数学(理科)试题内蒙古集宁一中(西校区)2019-2020学年高二下学期期末考试数学(理)试题西藏山南市第二高级中学2021届高三上学期第一次月考数学(文)试题(已下线)【新东方】杭州新东方高中数学试卷372上海市曹杨中学2020-2021学年高一上学期12月月考数学试题(已下线)4.2 指数函数(精讲)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教A版)(已下线)第三章 指数函数和对数函数(基础过关)-2020-2021学年高一数学单元测试定心卷(北师大版必修1) 黑龙江省哈尔滨市哈尔滨第九中学2021届高三下学期四模数学(文)试题黑龙江省哈尔滨市呼兰区第一中学校2021届高三下学期5月第四次模拟考试数学(文)试试题(已下线)第15讲 指数函数-【A+课堂】2021-2022学年高一数学同步精讲精练(沪教版2020必修第一册)(已下线)6.2指数函数(2)-2021-2022学年高一数学链接教材精准变式练(苏教版2019必修第一册)(已下线)第07讲 指数与指数函数(讲)- 2022年高考数学一轮复习讲练测(课标全国版)贵州省贵阳市五校(贵阳民中 贵阳九中 贵州省实验中学 贵阳二中 贵阳八中)2022届高三上学期联合考试(二)数学(文)试题贵州省贵阳市五校(贵阳民中 贵阳九中 贵州省实验中学 贵阳二中 贵阳八中)2022届高三上学期联合考试(二)数学(理)试题沪教版(2020) 必修第一册 堂堂清 第四章 复习检测四广东省广州市五中2021-2022学年高一上学期11月学段考数学试题(已下线)试卷20(第1章-7.1 角与弧度)2021-2022学年高一数学易错题、精典题滚动训练(苏教版2019必修第一册)(已下线)知识点02 指数函数-【提升专练】2021-2022学年高一数学新教材同步学案+课时对点练(苏教版2019必修第一册)四川省绵阳市绵阳第一中学2021-2022学年高一上学期期中数学试题广西柳州市第三中学2022届高三3月模热身考数学(理)试题广西柳州市第三中学2022届高三3月模热身考数学(文)试题2004 年普通高等学校招生考试数学(文)试题(湖南卷)沪教版(2020) 必修第一册 单元训练 第5章 单元测试(A卷)广东省广州外国语学校2022-2023学年高一上学期期末数学试题第三章 指数运算与指数函数 单元检测卷-2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)考点10 指数函数 2024届高考数学考点总动员【练】(已下线)第四章 幂函数、指数函数与对数函数(易错必刷30题11种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)专题07 函数解析式中的参变量----运动变化思想的应用(一题多变)黑龙江省大庆市第四中学2023-2024学年高二下学期7月期末数学试题单元测试B卷——第四章 指数函数与对数函数



