名校
解题方法
1 . 在空间直角坐标系 中,已知向量
中,已知向量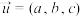 ,点
,点 .若直线
.若直线 以
以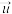 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为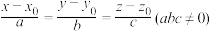 ;若平面
;若平面 以
以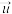 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为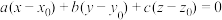 .
.
(1)已知直线 的标准式方程为
的标准式方程为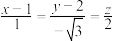 ,平面
,平面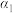 的点法式方程可表示为
的点法式方程可表示为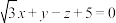 ,求直线
,求直线 与平面
与平面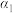 所成角的余弦值;
所成角的余弦值;
(2)已知平面 的点法式方程可表示为
的点法式方程可表示为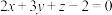 ,平面外一点
,平面外一点 ,点
,点 到平面
到平面 的距离;
的距离;
 中,已知向量
中,已知向量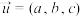 ,点
,点 .若直线
.若直线 以
以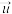 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为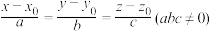 ;若平面
;若平面 以
以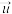 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程表示为
的点法式方程表示为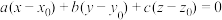 .
.(1)已知直线
 的标准式方程为
的标准式方程为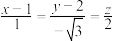 ,平面
,平面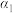 的点法式方程可表示为
的点法式方程可表示为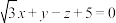 ,求直线
,求直线 与平面
与平面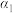 所成角的余弦值;
所成角的余弦值;(2)已知平面
 的点法式方程可表示为
的点法式方程可表示为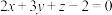 ,平面外一点
,平面外一点 ,点
,点 到平面
到平面 的距离;
的距离;
您最近一年使用:0次
2 . 如图,在平行四边形 中,
中,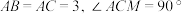 ,以
,以 为折痕将
为折痕将 折起,使点M到达点D的位置,且
折起,使点M到达点D的位置,且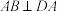 .
.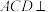 平面
平面 .
.
(2)Q为线段 上一点,P为线段
上一点,P为线段 上一点,且
上一点,且 ,求点P到平面ABQ的距离.
,求点P到平面ABQ的距离.
 中,
中,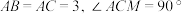 ,以
,以 为折痕将
为折痕将 折起,使点M到达点D的位置,且
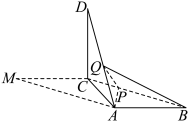
折起,使点M到达点D的位置,且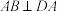 .
.
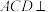 平面
平面 .
.(2)Q为线段
 上一点,P为线段
上一点,P为线段 上一点,且
上一点,且 ,求点P到平面ABQ的距离.
,求点P到平面ABQ的距离.
您最近一年使用:0次
名校
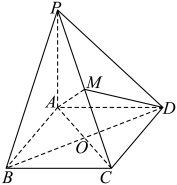
3 . 如图,在四棱锥 中,
中,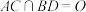 ,
, 与
与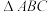 均是边长为
均是边长为 的正三角形,四边形
的正三角形,四边形 是平行四边形,二面角
是平行四边形,二面角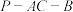 的平面角为
的平面角为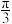 .
. ;
;
(2)若 为侧棱
为侧棱 的中点,求直线
的中点,求直线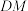 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,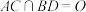 ,
, 与
与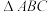 均是边长为
均是边长为 的正三角形,四边形
的正三角形,四边形 是平行四边形,二面角
是平行四边形,二面角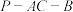 的平面角为
的平面角为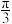 .
.
 ;
;(2)若
 为侧棱
为侧棱 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
解题方法
4 . 如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 是
是 的中点.
的中点.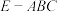 的体积;
的体积;
(2)求平面 与平面
与平面 夹角的余弦值;
夹角的余弦值;
(3)在棱 上是否存在一点
上是否存在一点 ,使直线
,使直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,若存在,求出求线段
,若存在,求出求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 是
是 的中点.
的中点.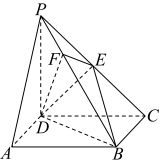
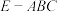 的体积;
的体积;(2)求平面
 与平面
与平面 夹角的余弦值;
夹角的余弦值;(3)在棱
 上是否存在一点
上是否存在一点 ,使直线
,使直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,若存在,求出求线段
,若存在,求出求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
您最近一年使用:0次
名校
5 . 在 中,
中,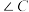 为直角,
为直角,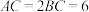 ,点
,点 分别在边
分别在边 和
和 上,且
上,且

 ,如图甲.将
,如图甲.将 沿
沿 折起到
折起到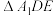 的位置,使
的位置,使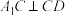 ,点
,点 在棱
在棱 上,如图乙.
上,如图乙.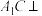 平面
平面 ;
;
(2)若 是
是 的中点,求
的中点,求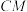 与平面
与平面 所成角的大小;
所成角的大小;
(3)若平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为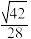 ,求
,求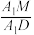 的值.
的值.
 中,
中,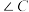 为直角,
为直角,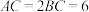 ,点
,点 分别在边
分别在边 和
和 上,且
上,且

 ,如图甲.将
,如图甲.将 沿
沿 折起到
折起到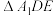 的位置,使
的位置,使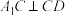 ,点
,点 在棱
在棱 上,如图乙.
上,如图乙.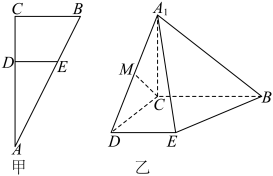
 平面
平面 ;
;(2)若
 是
是 的中点,求
的中点,求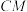 与平面
与平面 所成角的大小;
所成角的大小;(3)若平面
 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为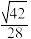 ,求
,求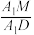 的值.
的值.
您最近一年使用:0次
解题方法
6 . 已知两个非零向量 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作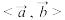 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
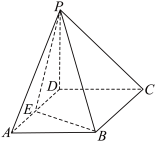
都垂直,它的模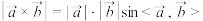 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 为
为 上一点,
上一点,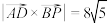 .
. 的长;
的长;
(2)若 为
为 的中点,求平面
的中点,求平面 与平面
与平面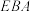 所成角的余弦值;
所成角的余弦值;
(3)若 为
为 上一点,且满足
上一点,且满足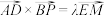 ,求
,求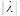 .
.
 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作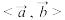 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
都垂直,它的模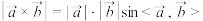 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 为
为 上一点,
上一点,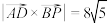 .
.
 的长;
的长;(2)若
 为
为 的中点,求平面
的中点,求平面 与平面
与平面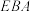 所成角的余弦值;
所成角的余弦值;(3)若
 为
为 上一点,且满足
上一点,且满足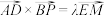 ,求
,求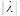 .
.
您最近一年使用:0次
2024-11-02更新
|
398次组卷
|
3卷引用:贵州省贵阳市六校联盟2024-2025学年高二上学期联合考试(一)(10月)数学试题
贵州省贵阳市六校联盟2024-2025学年高二上学期联合考试(一)(10月)数学试题辽宁省沈阳市部分学校2025届高三上学期第二次联合教学质量检测数学试题(已下线)阶段测5 周测14-周测16(高三一轮好卷基础卷)
7 . 如图所示,在三棱柱 中,
中, ,侧面
,侧面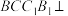 底面
底面 ,
, ,
, 分别为棱
分别为棱 和
和 的中点.
的中点. 平面
平面 ;
;
(2)若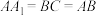 ,且平面
,且平面 平面
平面 ,求二面角
,求二面角 的余弦值大小.
的余弦值大小.
 中,
中, ,侧面
,侧面 底面
底面 ,
, ,
, 分别为棱
分别为棱 和
和 的中点.
的中点.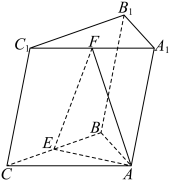
 平面
平面 ;
;(2)若
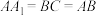 ,且平面
,且平面 平面
平面 ,求二面角
,求二面角 的余弦值大小.
的余弦值大小.
您最近一年使用:0次
2024-11-02更新
|
784次组卷
|
4卷引用:2025届湖南省衡阳市衡阳县高三一模数学试题
2025届湖南省衡阳市衡阳县高三一模数学试题(已下线)阶段测6周测14-周测18【实战演练】提升卷(已下线)第三节 直线、平面平行的判定与性质【讲】北京专版 江西省上饶市余干县第二中学2024-2025学年高二上学期10月检测数学试卷
8 . 如图,在三棱柱 中,
中,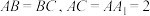 ,点
,点 为棱
为棱 的中点,平面
的中点,平面 平面
平面 ,且
,且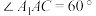 .(统一以
.(统一以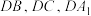 分别为
分别为 轴建立空间直角坐标系)
轴建立空间直角坐标系)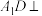 平面
平面 ;
;
(2)若 ,求二面角
,求二面角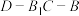 的正弦值
的正弦值
 中,
中,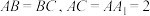 ,点
,点 为棱
为棱 的中点,平面
的中点,平面 平面
平面 ,且
,且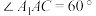 .(统一以
.(统一以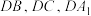 分别为
分别为 轴建立空间直角坐标系)
轴建立空间直角坐标系)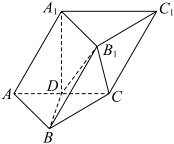
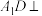 平面
平面 ;
;(2)若
 ,求二面角
,求二面角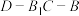 的正弦值
的正弦值
您最近一年使用:0次
名校
解题方法
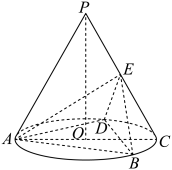
9 . 如图, 为圆锥的顶点,
为圆锥的顶点, 是圆锥底面的圆心,
是圆锥底面的圆心, 为底面直径,
为底面直径, 为底面圆
为底面圆 的内接正三角形,点
的内接正三角形,点 在母线
在母线 上,且
上,且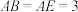 ,
,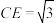 .
.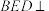 平面
平面 ;
;
(2)求直线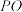 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)在线段 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为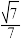 ?若存在,确定点
?若存在,确定点 的位置,若不存在,请说明理由
的位置,若不存在,请说明理由
 为圆锥的顶点,
为圆锥的顶点, 是圆锥底面的圆心,
是圆锥底面的圆心, 为底面直径,
为底面直径, 为底面圆
为底面圆 的内接正三角形,点
的内接正三角形,点 在母线
在母线 上,且
上,且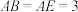 ,
,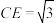 .
.
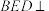 平面
平面 ;
;(2)求直线
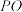 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在线段
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为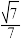 ?若存在,确定点
?若存在,确定点 的位置,若不存在,请说明理由
的位置,若不存在,请说明理由
您最近一年使用:0次
2024-11-02更新
|
1040次组卷
|
3卷引用:广东省深圳市深圳实验学校高中部2024-2025学年高二上学期第一阶段考试数学试卷
解题方法
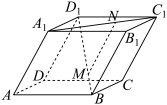
10 . 如图,在棱长均为1的四棱柱 中,
中, ,设
,设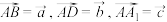 .
.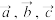 表示
表示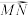 ;
;
(2)求 的长度;
的长度;
(3)求直线 与直线
与直线 所成角的余弦值.
所成角的余弦值.
 中,
中, ,设
,设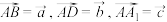 .
.
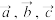 表示
表示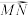 ;
;(2)求
 的长度;
的长度;(3)求直线
 与直线
与直线 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024-11-02更新
|
223次组卷
|
2卷引用:河南省洛阳市创新联盟发展2024-2025学年高二上学期第二次月考(10月)数学试题



