名校
解题方法
1 . 对于 ,定义
,定义 ,
,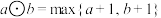 ,其中
,其中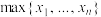 为
为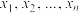 中最大的数,例如:
中最大的数,例如: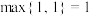 ,
,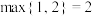 ,
, . 给定正整数
. 给定正整数 ,根据以上内容,对于
,根据以上内容,对于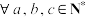 ,请回答下列问题:
,请回答下列问题:
(1)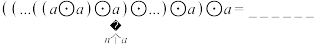 (用
(用 和
和 表示);
表示);
(2)满足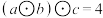 的有序数对
的有序数对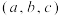 有多少个?
有多少个?
(3)满足 的有序数对
的有序数对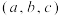 有多少个?
有多少个?
(4)满足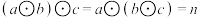 的有序数对
的有序数对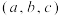 有多少个?
有多少个?
 ,定义
,定义 ,
,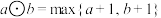 ,其中
,其中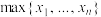 为
为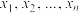 中最大的数,例如:
中最大的数,例如: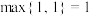 ,
,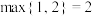 ,
, . 给定正整数
. 给定正整数 ,根据以上内容,对于
,根据以上内容,对于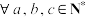 ,请回答下列问题:
,请回答下列问题:(1)
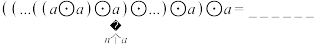 (用
(用 和
和 表示);
表示);(2)满足
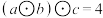 的有序数对
的有序数对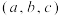 有多少个?
有多少个?(3)满足
 的有序数对
的有序数对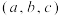 有多少个?
有多少个?(4)满足
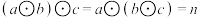 的有序数对
的有序数对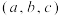 有多少个?
有多少个?
您最近一年使用:0次
名校
解题方法
2 . 在下面两个条件中任选一个,补充到下面的问题中,并对其求解.
条件①: ;条件②:
;条件②: .
.
问题:已知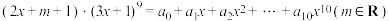 ,若__________.
,若__________.
(1)求实数 的值;
的值;
(2)求 的值.
的值.
条件①:
 ;条件②:
;条件②: .
.问题:已知
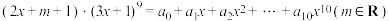 ,若__________.
,若__________.(1)求实数
 的值;
的值;(2)求
 的值.
的值.
您最近一年使用:0次
3 . 唐诗是中国古典文化最灿烂的瑰宝之一.2023年7月8日,电影《长安三万里》上映以来,全国掀起了诗词背诵的狂潮,在电影院背诗成了当下最常见的现象,某诗词协会为了了解观众对影片中出现的48首唐诗的熟悉情况(若会背诵其中40首唐诗为极熟悉,否则为不太熟悉),在影片放映结束后,随机抽取了200位观众进行调查,得到如下2×2列联表:
附: ,
, .
.
(1)补全2×2列联表
(2)是否有97.5%的把握认为对这48首唐诗的熟悉程度与年龄有关?
(3)按分层随机抽样的方式在极熟悉48首唐诗的观众中抽取6人进行唐诗小调查,随后再从这6人中抽取3人进行唐诗接力赛,记3人中年龄超过30岁的人数为X,求X的分布列与均值
| 对48首唐诗极熟悉 | 对48首唐诗不太熟悉 | 总计 | |
| 不超过30岁 | 80 | 120 | |
| 超过30岁 | 40 | ||
| 总计 |
 ,
, .
.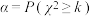 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)是否有97.5%的把握认为对这48首唐诗的熟悉程度与年龄有关?
(3)按分层随机抽样的方式在极熟悉48首唐诗的观众中抽取6人进行唐诗小调查,随后再从这6人中抽取3人进行唐诗接力赛,记3人中年龄超过30岁的人数为X,求X的分布列与均值
您最近一年使用:0次
名校
解题方法
4 . 一次知识竞赛中,共有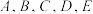 五道题,参赛人从中抽出三道题回答,每题的分值如下:
五道题,参赛人从中抽出三道题回答,每题的分值如下:
答对该试题可得相应的分值,答错不得分,得分不低于60分可以获奖.已知参赛人甲答对 题的概率为
题的概率为 ,答对
,答对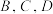 题的概率均为
题的概率均为 ,答对E题的概率为
,答对E题的概率为 ,则甲能获奖的概率为( )
,则甲能获奖的概率为( )
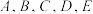 五道题,参赛人从中抽出三道题回答,每题的分值如下:
五道题,参赛人从中抽出三道题回答,每题的分值如下:
|
|
|
|
| |
分值 | 10 | 20 | 20 | 20 | 30 |
 题的概率为
题的概率为 ,答对
,答对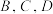 题的概率均为
题的概率均为 ,答对E题的概率为
,答对E题的概率为 ,则甲能获奖的概率为( )
,则甲能获奖的概率为( )A.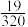 | B. | C.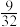 | D. |
您最近一年使用:0次
2024-06-04更新
|
107次组卷
|
2卷引用:河北省保定市部分学校2023-2024学年高二下学期5月期中考试数学试题
名校
解题方法
5 . 某校为了给高三学生举办“18岁成人礼”活动,由团委草拟了活动方案,并以问卷的形式调查了部分同学对活动方案的评分(满分100分),所得评分统计如图所示. 的人数为
的人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.
(2)为了解评分是否与性别有关,随机抽取了部分问卷,统计结果如下表所示,则依据 的独立性检验,能否认为评分与性别有关?
的独立性检验,能否认为评分与性别有关?
(3)若将(2)中表格的人数数据都扩大为原来的10倍,则依据 的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
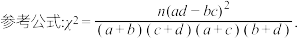
参考数据:
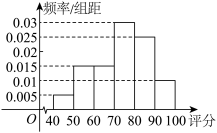
 的人数为
的人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.(2)为了解评分是否与性别有关,随机抽取了部分问卷,统计结果如下表所示,则依据
 的独立性检验,能否认为评分与性别有关?
的独立性检验,能否认为评分与性别有关?| 男生 | 女生 | |
评分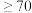 | 30 | 35 |
评分 | 20 | 15 |
(3)若将(2)中表格的人数数据都扩大为原来的10倍,则依据
 的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.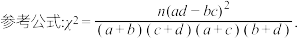
参考数据:
 | 0.1 | 0.05 | 0.01 |
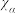 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
名校
6 . 为贯彻落实《健康中国行动(2023-2030年)》、《关于全面加强和改进新时代学校体育工作的意见》等文件精神,某高中学校学生发展中心随机抽查了100名学生,其中男生与女生人数之比为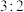 ,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
(1)请根据要求完成 列联表,并根据独立性检验,判断是否有
列联表,并根据独立性检验,判断是否有 的把握认为“是否喜欢体育运动”与性别有关;
的把握认为“是否喜欢体育运动”与性别有关;
(2)为了了解学生不喜欢体育运动的原因,从上述不喜欢体育运动的同学中随机选3位同学进行咨询,所选的3人中已知至少有两位是男生的条件下,求另外一位是女生的概率.
参考公式: .
.
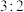 ,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:
,并对他们进行了“是否喜欢体育运动”的问卷调查,得到如下统计结果:| 性别 | 体育运动 | 合计 | |
| 喜欢 | 不喜欢 | ||
| 男生 | 50 | ||
| 女生 | 15 | ||
| 合计 | |||
 列联表,并根据独立性检验,判断是否有
列联表,并根据独立性检验,判断是否有 的把握认为“是否喜欢体育运动”与性别有关;
的把握认为“是否喜欢体育运动”与性别有关;(2)为了了解学生不喜欢体育运动的原因,从上述不喜欢体育运动的同学中随机选3位同学进行咨询,所选的3人中已知至少有两位是男生的条件下,求另外一位是女生的概率.
参考公式:
 .
. | 0.10 | 0.05 | 0.01 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
名校
解题方法
7 . 在一个阳光明媚的周末,市射击俱乐部举办了一场盛大的射击比赛,来自各地的射击爱好者纷纷报名参加,甲乙作为一个组合报名参加了射击小组赛.该项比赛规则为:每个小组2人,每人每轮依次射击一次,共有2轮.若两人合计射中靶心次数不少于3次,则称这组为“神枪手组合”.已知甲、乙射中靶心的概率分别为 和
和 ,若
,若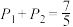 ,那么甲乙小组最后获得“神枪手组合”称号的最大可能性为
,那么甲乙小组最后获得“神枪手组合”称号的最大可能性为________ (假设所有选手每次射击都互相独立).
 和
和 ,若
,若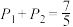 ,那么甲乙小组最后获得“神枪手组合”称号的最大可能性为
,那么甲乙小组最后获得“神枪手组合”称号的最大可能性为
您最近一年使用:0次
名校
8 . 贵州省“美丽乡村”篮球联赛在比赛间隙进行芦笙舞、侗族大歌等非物质文化遗产展演,这项活动将体育运动与当地民族民俗文化相触合,创造出独特的文体公共产品.为了打造更具吸引力的赛事,某平台发起了群众观赛意见反馈调查,共收回了200份调查问卷.
(1)通过进一步分析关注赛事群众的调查问卷得知,关注表演的女性用户有24名,现从关注赛事的群众中抽取一人,设“抽取的一人为男性”为事件A,“抽取的一人关注表演”为事件B,若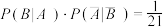 ,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
(2)是否有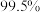 的把握认为是否关注赛事与性别有关?
的把握认为是否关注赛事与性别有关?
附: ,其中
,其中 .
.
性别 | 关注赛事 | 不关注赛事 |
男 | 84 | 36 |
女 | 40 | 40 |
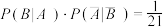 ,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;(2)是否有
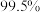 的把握认为是否关注赛事与性别有关?
的把握认为是否关注赛事与性别有关?附:
 ,其中
,其中 .
.
| 0.050 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
9 . 若m, ,
, ,
,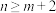 ,则
,则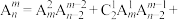
_____________ .(请用一个排列数来表示)
 ,
, ,
,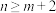 ,则
,则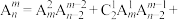
您最近一年使用:0次
名校
解题方法
10 . 在探究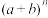 的展开式的二项式系数性质时,我们把系数列成一张表,借助它发现了一些规律.在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中,出现了这个表,我们称这个表为杨辉三角.杨辉三角是中国古代数学中十分精彩的篇章.杨辉三角如下图所示:
的展开式的二项式系数性质时,我们把系数列成一张表,借助它发现了一些规律.在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中,出现了这个表,我们称这个表为杨辉三角.杨辉三角是中国古代数学中十分精彩的篇章.杨辉三角如下图所示:
第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
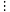
如上图,杨辉三角第6行的7个数依次为 ,
,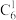 ,
, …
…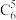 ,
, .现将杨辉三角中第
.现将杨辉三角中第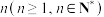 行的第
行的第 个数乘以
个数乘以 ,第0行的一个数为0,得到一个新的三角数阵如下图:
,第0行的一个数为0,得到一个新的三角数阵如下图:
第0行 0
第1行 0 1
第2行 0 2 2
第3行 0 3 6 3
第4行 0 4 12 12 4
第5行 0 5 20 30 20 5
第6行 0 6 30 60 60 30 6
在这个新的三角数阵中,第10行的第3个数为________ ;从第一行开始的前 行的所有数的和为
行的所有数的和为________ .
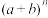 的展开式的二项式系数性质时,我们把系数列成一张表,借助它发现了一些规律.在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中,出现了这个表,我们称这个表为杨辉三角.杨辉三角是中国古代数学中十分精彩的篇章.杨辉三角如下图所示:
的展开式的二项式系数性质时,我们把系数列成一张表,借助它发现了一些规律.在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中,出现了这个表,我们称这个表为杨辉三角.杨辉三角是中国古代数学中十分精彩的篇章.杨辉三角如下图所示:第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
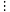
如上图,杨辉三角第6行的7个数依次为
 ,
,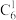 ,
, …
…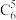 ,
, .现将杨辉三角中第
.现将杨辉三角中第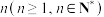 行的第
行的第 个数乘以
个数乘以 ,第0行的一个数为0,得到一个新的三角数阵如下图:
,第0行的一个数为0,得到一个新的三角数阵如下图:第0行 0
第1行 0 1
第2行 0 2 2
第3行 0 3 6 3
第4行 0 4 12 12 4
第5行 0 5 20 30 20 5
第6行 0 6 30 60 60 30 6
在这个新的三角数阵中,第10行的第3个数为
 行的所有数的和为
行的所有数的和为
您最近一年使用:0次








