名校
解题方法
1 . 新高考数学试卷出现多项选择题,即每小题的四个选项中,有多项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.若正确答案为两项,每对一项得3分:若正确答案为三项,每对一项得2分;
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:
若此题的正确选项为AC.求学生甲答此题得6分的概率:
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为 ,正确答案是三个选项的概率为
,正确答案是三个选项的概率为 (
( ).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
①若 ,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
②以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好?
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:
| 选项 | 作出正确判断 | 判断不了(不选) | 作出错误判断 |
| A | 0.8 | 0.1 | 0.1 |
| B | 0.7 | 0.1 | 0.2 |
| C | 0.6 | 0.3 | 0.1 |
| D | 0.5 | 0.3 | 0.2 |
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为
 ,正确答案是三个选项的概率为
,正确答案是三个选项的概率为 (
( ).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.①若
 ,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.②以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好?
您最近一年使用:0次
2 . 将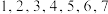 这七个数随机地排成一个数列,记第i项为
这七个数随机地排成一个数列,记第i项为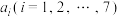 ,则下列说法正确的是( )
,则下列说法正确的是( )
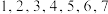 这七个数随机地排成一个数列,记第i项为
这七个数随机地排成一个数列,记第i项为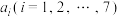 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若 , ,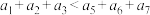 ,则这样的数列共有360个 ,则这样的数列共有360个 |
| B.若该数列恰好先增后减,则这样的数列共有64个 |
| C.若所有的奇数不相邻,所有的偶数也不相邻,则这样的数列共有144个 |
D.若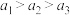 , ,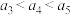 , ,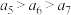 ,则这样的数列共有71个 ,则这样的数列共有71个 |
您最近一年使用:0次
解题方法
3 . 三个人猜拳决定胜利者,三个人分别可以出“石头”,“剪刀”,“布”,其中“石头”赢“剪刀”,“剪刀”赢“布”,“布”赢“石头”,例如,当一个人出“布”,另两个人出“石头”时,只用一回正好决定胜利者;当一人出“石头”,另两人出“布”时,则淘汰出“石头”的人,三人猜拳输的人被淘汰,直到决出一个胜利者为止.
(1)求一次猜拳决出胜利者的概率;
(2)求在第 回猜拳决出胜利者的概率.
回猜拳决出胜利者的概率.
(1)求一次猜拳决出胜利者的概率;
(2)求在第
 回猜拳决出胜利者的概率.
回猜拳决出胜利者的概率.
您最近一年使用:0次
4 . 已知函数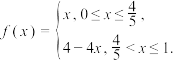 随机变量
随机变量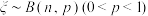 ,随机变量
,随机变量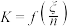 ,
, 的期望为
的期望为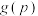 .
.
(1)当 时,求
时,求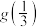 ;
;
(2)当 时,求
时,求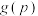 的表达式.
的表达式.
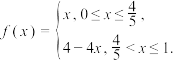 随机变量
随机变量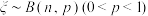 ,随机变量
,随机变量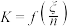 ,
, 的期望为
的期望为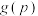 .
.(1)当
 时,求
时,求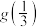 ;
;(2)当
 时,求
时,求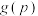 的表达式.
的表达式.
您最近一年使用:0次
2024-06-16更新
|
411次组卷
|
4卷引用:河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)
河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)(已下线)辽宁省沈阳市第二中学2024届高三下学期三模数学试题内蒙古自治区锡林郭勒盟2024届高三下学期5月模拟考试理科数学试题(已下线)概率、随机变量及其分布-综合测试卷B卷
名校
解题方法
5 . 切比雪夫不等式是19世纪俄国数学家切比雪夫(1821.5~1894.12)在研究统计规律时发现的,其内容是:对于任一随机变量 ,若其数学期望
,若其数学期望 和方差
和方差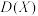 均存在,则对任意正实数
均存在,则对任意正实数 ,有
,有 .根据该不等式可以对事件
.根据该不等式可以对事件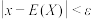 的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号
的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号 次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量
次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量 ,为了至少有
,为了至少有 的把握使发射信号“1”的频率在区间
的把握使发射信号“1”的频率在区间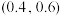 内,估计信号发射次数
内,估计信号发射次数 的值至少为
的值至少为______ .
 ,若其数学期望
,若其数学期望 和方差
和方差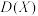 均存在,则对任意正实数
均存在,则对任意正实数 ,有
,有 .根据该不等式可以对事件
.根据该不等式可以对事件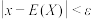 的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号
的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号 次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量
次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量 ,为了至少有
,为了至少有 的把握使发射信号“1”的频率在区间
的把握使发射信号“1”的频率在区间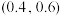 内,估计信号发射次数
内,估计信号发射次数 的值至少为
的值至少为
您最近一年使用:0次
2024-06-11更新
|
758次组卷
|
9卷引用:辽宁省沈阳市第二中学2024届高三第五次模拟考试数学试题
辽宁省沈阳市第二中学2024届高三第五次模拟考试数学试题(已下线)第3套 期末全真模拟卷(高二期末基础卷)(已下线)高二数学下学期期末押题卷01-2023-2024学年高二数学同步讲与练(人教A版2019)山东省部分学校2023-2024学年高二下学期期末联合教学质量检测数学试卷山东省泰安市部分学校2023-2024学年高二下学期期末测试数学试题山东省齐鲁名师联盟2025届高三上学期第一次诊断考试数学试题宁夏回族自治区银川一中2025届高三上学期八月开学复习巩固测试数学试题河南省驻马店市新蔡县第一高级中学2025届高三上学期8月开学考试数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】
6 . 在足球比赛中,有时需通过点球决定胜负.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将(也称为守门员)也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数 的分布列和期望;
的分布列和期望;
(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外 人中的
人中的  人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能接住.记第
人,如此不停地传下去,假设传出的球都能接住.记第 次传球之前球在甲脚下的概率为
次传球之前球在甲脚下的概率为 ,易知
,易知 .
.
① 试证明: 为等比数列;
为等比数列;
② 设第 次传球之前球在乙脚下的概率为
次传球之前球在乙脚下的概率为 ,比较
,比较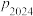 与
与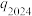 的大小.
的大小.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将(也称为守门员)也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有
 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数 的分布列和期望;
的分布列和期望;(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外
 人中的
人中的  人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能接住.记第
人,如此不停地传下去,假设传出的球都能接住.记第 次传球之前球在甲脚下的概率为
次传球之前球在甲脚下的概率为 ,易知
,易知 .
.① 试证明:
 为等比数列;
为等比数列;② 设第
 次传球之前球在乙脚下的概率为
次传球之前球在乙脚下的概率为 ,比较
,比较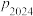 与
与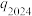 的大小.
的大小.
您最近一年使用:0次
名校
7 . 知识卡片:一般地,如果 是区间
是区间 上的连续函数,并且
上的连续函数,并且 ,那么
,那么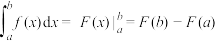 .这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.当
.这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.当 ,
,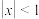 时,有如下表达式:
时,有如下表达式: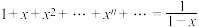 ,两边同时积分得:
,两边同时积分得: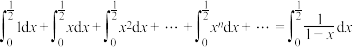 ,从而得到如下等式:
,从而得到如下等式: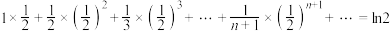 请根据以上材料所蕴含的数学思想方法,由二项式定理
请根据以上材料所蕴含的数学思想方法,由二项式定理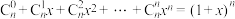 计算:
计算: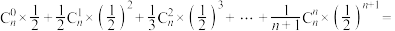
_______ .
 是区间
是区间 上的连续函数,并且
上的连续函数,并且 ,那么
,那么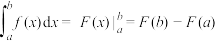 .这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.当
.这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.当 ,
,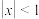 时,有如下表达式:
时,有如下表达式: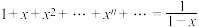 ,两边同时积分得:
,两边同时积分得: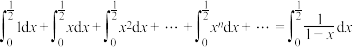 ,从而得到如下等式:
,从而得到如下等式: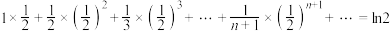 请根据以上材料所蕴含的数学思想方法,由二项式定理
请根据以上材料所蕴含的数学思想方法,由二项式定理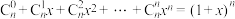 计算:
计算: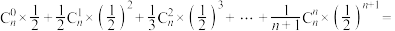
您最近一年使用:0次
2024-06-07更新
|
300次组卷
|
3卷引用:湖北省襄阳第四中学2024届高三下学期五月高考适应性考试(二)数学试卷
解题方法
8 . 甲、乙两同学进行射击比赛,已知甲射击一次命中的概率为 ,乙射击一次命中的概率为
,乙射击一次命中的概率为 ,比赛共进行n轮次,且每次射击结果相互独立,现有两种比赛方案,方案一:射击n次,每次命中得2分,未命中得0分;方案二:从第一次射击开始,若本次命中,则得6分,并继续射击;若本次未命中,则得0分,并终止射击.
,比赛共进行n轮次,且每次射击结果相互独立,现有两种比赛方案,方案一:射击n次,每次命中得2分,未命中得0分;方案二:从第一次射击开始,若本次命中,则得6分,并继续射击;若本次未命中,则得0分,并终止射击.
(1)设甲同学在方案一中射击n轮次总得分为随机变量是 ,求
,求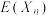 ;
;
(2)设乙同学选取方案二进行比赛,乙同学的总得分为随机变量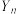 ,求
,求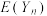 ;
;
(3)甲同学选取方案一、乙同学选取方案二进行比赛,试确定N的最小值,使得当 时,甲的总得分期望大于乙.
时,甲的总得分期望大于乙.
 ,乙射击一次命中的概率为
,乙射击一次命中的概率为 ,比赛共进行n轮次,且每次射击结果相互独立,现有两种比赛方案,方案一:射击n次,每次命中得2分,未命中得0分;方案二:从第一次射击开始,若本次命中,则得6分,并继续射击;若本次未命中,则得0分,并终止射击.
,比赛共进行n轮次,且每次射击结果相互独立,现有两种比赛方案,方案一:射击n次,每次命中得2分,未命中得0分;方案二:从第一次射击开始,若本次命中,则得6分,并继续射击;若本次未命中,则得0分,并终止射击.(1)设甲同学在方案一中射击n轮次总得分为随机变量是
 ,求
,求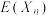 ;
;(2)设乙同学选取方案二进行比赛,乙同学的总得分为随机变量
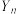 ,求
,求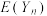 ;
;(3)甲同学选取方案一、乙同学选取方案二进行比赛,试确定N的最小值,使得当
 时,甲的总得分期望大于乙.
时,甲的总得分期望大于乙.
您最近一年使用:0次
名校
解题方法
9 . 某人在 次射击中击中目标的次数为
次射击中击中目标的次数为 ,
,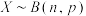 ,其中
,其中 ,
, ,击中奇数次为事件
,击中奇数次为事件 ,则( )
,则( )
 次射击中击中目标的次数为
次射击中击中目标的次数为 ,
,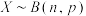 ,其中
,其中 ,
, ,击中奇数次为事件
,击中奇数次为事件 ,则( )
,则( )A.若 , ,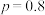 ,则 ,则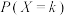 取最大值时 取最大值时 |
B.当 时, 时, 取得最小值 取得最小值 |
C.当 时, 时,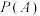 随着 随着 的增大而增大 的增大而增大 |
D.当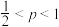 时, 时,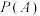 随着 随着 的增大而减小 的增大而减小 |
您最近一年使用:0次
2024-06-01更新
|
428次组卷
|
22卷引用:山东省泰安肥城市2023届高考适应性训练数学试题(三)
山东省泰安肥城市2023届高考适应性训练数学试题(三)山东省新高考质量检测联盟2024届高三第一次质量检测数学试题(A)(已下线)模块一 专题2 概率(北师大2019版)(已下线)模块一 专题4 随机变量及其分布 (人教A)(已下线)模块一 专题3 概率 (苏教版)(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练(已下线)单元提升卷11 统计与概率湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题(已下线)考点13 二项分布与超级几何分布 2024届高考数学考点总动员【练】(已下线)第11讲 二项分布与超几何分布-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)随机变量及其分布(已下线)专题04 超几何分布+二项分布+正态分布压轴题(4)(已下线)7.4.1 二项分布(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)黄金卷02(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-1辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题(已下线)高二下期末考前押题卷02--高二期末考点大串讲(人教B版2019选择性必修)(已下线)概率、随机变量及其分布-综合测试卷A卷(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】
名校
10 . 第二次世界大战期间,了解德军坦克的生产能力对盟军具有非常重要的战略意义.已知德军的每辆坦克上都有一个按生产顺序从1开始的连续编号.假设德军某月生产的坦克总数为N,随机缴获该月生产的n辆( )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记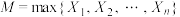 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
甲同学根据样本均值估计总体均值的思想,用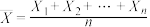 估计总体的均值,因此
估计总体的均值,因此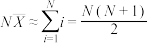 ,得
,得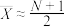 ,故可用
,故可用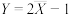 作为N的估计.
作为N的估计.
乙同学对此提出异议,认为这种方法可能出现 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若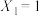 ,
,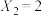 ,
,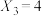 ,则
,则 ,此时
,此时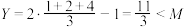 .
.
(1)当 ,
, 时,求条件概率
时,求条件概率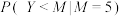 ;
;
(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;
(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
 )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记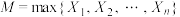 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.甲同学根据样本均值估计总体均值的思想,用
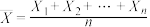 估计总体的均值,因此
估计总体的均值,因此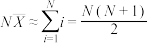 ,得
,得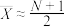 ,故可用
,故可用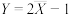 作为N的估计.
作为N的估计.乙同学对此提出异议,认为这种方法可能出现
 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若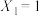 ,
,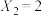 ,
,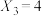 ,则
,则 ,此时
,此时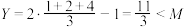 .
.(1)当
 ,
, 时,求条件概率
时,求条件概率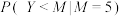 ;
;(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当
 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现
 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
您最近一年使用:0次
2024-05-28更新
|
1062次组卷
|
4卷引用:浙江省(杭州二中、绍兴一中、温州中学、金华一中、衢州二中)五校联考2024届高考数学模拟卷



