1 . 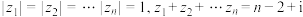 ,求
,求 的值.
的值.
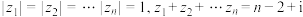 ,求
,求 的值.
的值.
您最近一年使用:0次
2 . 将正整数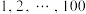 填入
填入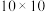 方格表中,每个小方格恰好填1个数,要求每行从左到右10个数依次递减,记第
方格表中,每个小方格恰好填1个数,要求每行从左到右10个数依次递减,记第 行的10个数之和为
行的10个数之和为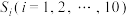 . 设
. 设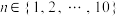 满足:存在一种填法,使得
满足:存在一种填法,使得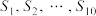 均大于第
均大于第 列上的10个数之和,求
列上的10个数之和,求 的最小值.
的最小值.
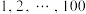 填入
填入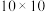 方格表中,每个小方格恰好填1个数,要求每行从左到右10个数依次递减,记第
方格表中,每个小方格恰好填1个数,要求每行从左到右10个数依次递减,记第 行的10个数之和为
行的10个数之和为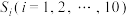 . 设
. 设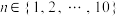 满足:存在一种填法,使得
满足:存在一种填法,使得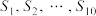 均大于第
均大于第 列上的10个数之和,求
列上的10个数之和,求 的最小值.
的最小值.
您最近一年使用:0次
3 . 数列 满足:
满足: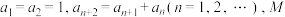 是大于1的正整数,试证明:在数列
是大于1的正整数,试证明:在数列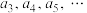 中存在相邻的两项,它们除以
中存在相邻的两项,它们除以 余数相同.
余数相同.
 满足:
满足: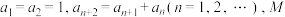 是大于1的正整数,试证明:在数列
是大于1的正整数,试证明:在数列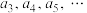 中存在相邻的两项,它们除以
中存在相邻的两项,它们除以 余数相同.
余数相同.
您最近一年使用:0次
4 . 求所有正整数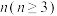 ,满足正
,满足正 边形能内接于平面直角坐标系
边形能内接于平面直角坐标系 中椭圆
中椭圆 .
.
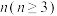 ,满足正
,满足正 边形能内接于平面直角坐标系
边形能内接于平面直角坐标系 中椭圆
中椭圆 .
.
您最近一年使用:0次
解题方法
5 . 如果 是离散型随机变量,则
是离散型随机变量,则 在
在 事件下的期望满足
事件下的期望满足 其中
其中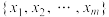 是
是 所有可能取值的集合.已知某独立重复试验的成功概率为
所有可能取值的集合.已知某独立重复试验的成功概率为 ,进行
,进行 次试验,求第
次试验,求第 次试验恰好是第二次成功的条件下,第一次成功的试验次数
次试验恰好是第二次成功的条件下,第一次成功的试验次数 的数学期望是
的数学期望是__________ .
 是离散型随机变量,则
是离散型随机变量,则 在
在 事件下的期望满足
事件下的期望满足 其中
其中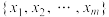 是
是 所有可能取值的集合.已知某独立重复试验的成功概率为
所有可能取值的集合.已知某独立重复试验的成功概率为 ,进行
,进行 次试验,求第
次试验,求第 次试验恰好是第二次成功的条件下,第一次成功的试验次数
次试验恰好是第二次成功的条件下,第一次成功的试验次数 的数学期望是
的数学期望是
您最近一年使用:0次
6 . 已知 是定义在
是定义在 上单调递增且图像连续不断的函数,且有
上单调递增且图像连续不断的函数,且有 ,设
,设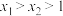 ,则下列说法正确的是( )
,则下列说法正确的是( )
 是定义在
是定义在 上单调递增且图像连续不断的函数,且有
上单调递增且图像连续不断的函数,且有 ,设
,设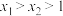 ,则下列说法正确的是( )
,则下列说法正确的是( )A.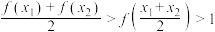 |
B.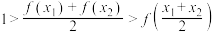 |
C. |
D. |
您最近一年使用:0次
7 . 若数列 满足对任意
满足对任意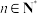 ,数列
,数列 的前
的前 项至少有
项至少有 项大于
项大于 ,且
,且 ,则称数列
,则称数列 具有性质
具有性质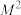 .若存在具有性质
.若存在具有性质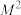 的数列
的数列 ,使得其前n项和
,使得其前n项和 恒成立,则
恒成立,则整数  的最小值是
的最小值是_____________ .
 满足对任意
满足对任意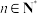 ,数列
,数列 的前
的前 项至少有
项至少有 项大于
项大于 ,且
,且 ,则称数列
,则称数列 具有性质
具有性质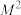 .若存在具有性质
.若存在具有性质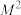 的数列
的数列 ,使得其前n项和
,使得其前n项和 恒成立,则
恒成立,则 的最小值是
的最小值是
您最近一年使用:0次
8 . A,B,C为 内角,x,y,z为实数,求以下三式中恒成立的个数.
内角,x,y,z为实数,求以下三式中恒成立的个数.
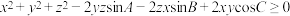
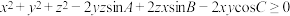
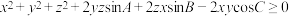
 内角,x,y,z为实数,求以下三式中恒成立的个数.
内角,x,y,z为实数,求以下三式中恒成立的个数.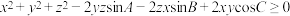
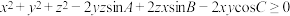
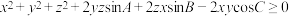
您最近一年使用:0次
解题方法
9 . 对集合 ,定义其特征函数
,定义其特征函数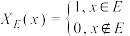 ,考虑集合
,考虑集合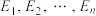 和正实数
和正实数 ,定义
,定义 为
为 和式函数.设
和式函数.设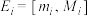 ,则
,则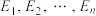 为闭区间列;如果集合
为闭区间列;如果集合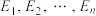 对任意
对任意 ,有
,有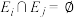 ,则称
,则称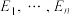 是无交集合列,设集合
是无交集合列,设集合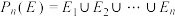 .
.
(1)证明:L和式函数的值域为有限集合;
(2)设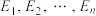 为闭区间列,
为闭区间列,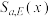 是定义在
是定义在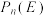 上的函数.已知存在唯一的正整数
上的函数.已知存在唯一的正整数 ,各项不同的非零实数
,各项不同的非零实数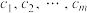 ,和无交集合列
,和无交集合列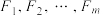 使得
使得 ,并且
,并且 ,称
,称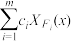 为
为 和式函数
和式函数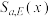 的典范形式.设
的典范形式.设 为
为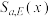 的典范数.
的典范数.
(i)设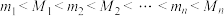 ,证明:
,证明: ;
;
(ii)给定正整数 ,任取正实数
,任取正实数 和闭区间列
和闭区间列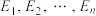 ,判断
,判断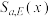 的典范数
的典范数 最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
 ,定义其特征函数
,定义其特征函数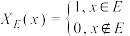 ,考虑集合
,考虑集合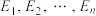 和正实数
和正实数 ,定义
,定义 为
为 和式函数.设
和式函数.设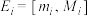 ,则
,则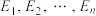 为闭区间列;如果集合
为闭区间列;如果集合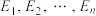 对任意
对任意 ,有
,有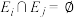 ,则称
,则称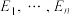 是无交集合列,设集合
是无交集合列,设集合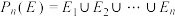 .
.(1)证明:L和式函数的值域为有限集合;
(2)设
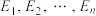 为闭区间列,
为闭区间列,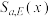 是定义在
是定义在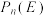 上的函数.已知存在唯一的正整数
上的函数.已知存在唯一的正整数 ,各项不同的非零实数
,各项不同的非零实数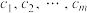 ,和无交集合列
,和无交集合列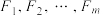 使得
使得 ,并且
,并且 ,称
,称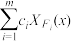 为
为 和式函数
和式函数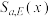 的典范形式.设
的典范形式.设 为
为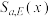 的典范数.
的典范数.(i)设
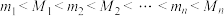 ,证明:
,证明: ;
;(ii)给定正整数
 ,任取正实数
,任取正实数 和闭区间列
和闭区间列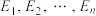 ,判断
,判断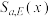 的典范数
的典范数 最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
您最近一年使用:0次
10 . 设有两个集合 ,如果对任意
,如果对任意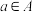 ,存在唯一的
,存在唯一的 ,满足
,满足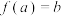 ,那么称
,那么称 是一个
是一个 的函数.设
的函数.设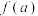 是
是 的函数,
的函数, 是
是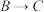 的函数,那么
的函数,那么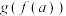 是
是 的函数,称为
的函数,称为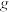 和
和 的复合,记为
的复合,记为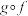 .如果两个
.如果两个 的函数
的函数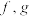 对任意
对任意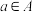 ,都有
,都有 ,则称
,则称 .
.
(1)对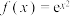 ,分别求一个
,分别求一个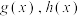 ,使得
,使得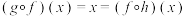 对全体
对全体 恒成立;
恒成立;
(2)设集合 和
和 的函数
的函数 以及
以及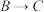 的函数
的函数 .
.
(i)对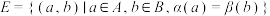 ,构造
,构造 的函数
的函数 以及
以及 的函数
的函数 ,满足
,满足 ;
;
(ii)对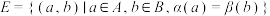 ,构造
,构造 的函数
的函数 以及
以及 的函数
的函数 ,满足
,满足 ,并且说明如果存在其它的集合
,并且说明如果存在其它的集合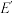 满足存在
满足存在 的函数
的函数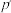 以及
以及 的函数
的函数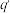 ,满足
,满足 ,则存在唯一的
,则存在唯一的 的函数
的函数 满足
满足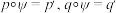 .
.
 ,如果对任意
,如果对任意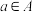 ,存在唯一的
,存在唯一的 ,满足
,满足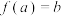 ,那么称
,那么称 是一个
是一个 的函数.设
的函数.设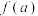 是
是 的函数,
的函数, 是
是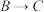 的函数,那么
的函数,那么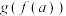 是
是 的函数,称为
的函数,称为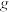 和
和 的复合,记为
的复合,记为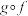 .如果两个
.如果两个 的函数
的函数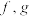 对任意
对任意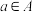 ,都有
,都有 ,则称
,则称 .
.(1)对
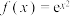 ,分别求一个
,分别求一个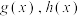 ,使得
,使得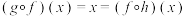 对全体
对全体 恒成立;
恒成立;(2)设集合
 和
和 的函数
的函数 以及
以及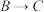 的函数
的函数 .
.(i)对
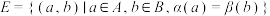 ,构造
,构造 的函数
的函数 以及
以及 的函数
的函数 ,满足
,满足 ;
;(ii)对
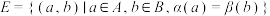 ,构造
,构造 的函数
的函数 以及
以及 的函数
的函数 ,满足
,满足 ,并且说明如果存在其它的集合
,并且说明如果存在其它的集合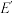 满足存在
满足存在 的函数
的函数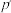 以及
以及 的函数
的函数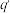 ,满足
,满足 ,则存在唯一的
,则存在唯一的 的函数
的函数 满足
满足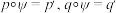 .
.
您最近一年使用:0次



