解题方法
1 . 已知函数 ,
,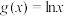 .
.
(1)若 是方程
是方程 的根,证明
的根,证明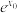 是方程
是方程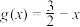 的根;
的根;
(2)设方程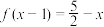 ,
, 的根分别是
的根分别是 ,
, ,求证:
,求证: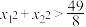 .
.
 ,
,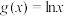 .
.(1)若
 是方程
是方程 的根,证明
的根,证明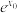 是方程
是方程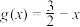 的根;
的根;(2)设方程
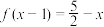 ,
, 的根分别是
的根分别是 ,
, ,求证:
,求证: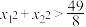 .
.
您最近一年使用:0次
解题方法
2 . 已知连续不断函数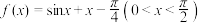 ,
,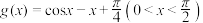 .
.
(1)求证:函数 在区间
在区间 上有且只有一个零点;
上有且只有一个零点;
(2)现已知函数 在
在 上有且只有一个零点(不必证明),记
上有且只有一个零点(不必证明),记 和
和 在
在 上的零点分别为
上的零点分别为 ,试求
,试求 的值.
的值.
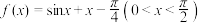 ,
,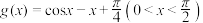 .
.(1)求证:函数
 在区间
在区间 上有且只有一个零点;
上有且只有一个零点;(2)现已知函数
 在
在 上有且只有一个零点(不必证明),记
上有且只有一个零点(不必证明),记 和
和 在
在 上的零点分别为
上的零点分别为 ,试求
,试求 的值.
的值.
您最近一年使用:0次
2021-01-31更新
|
290次组卷
|
3卷引用:湖北省鄂东南新高考联盟2020-2021学年高一上学期期末联考数学试题
名校
3 . 已知函数
(1)若 ,求证:函数
,求证:函数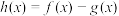 恰有一个正零点;(用图像法证明不给分)
恰有一个正零点;(用图像法证明不给分)
(2)若函数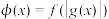 恰有三个零点,求实数
恰有三个零点,求实数 取值范围.
取值范围.

(1)若
 ,求证:函数
,求证:函数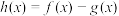 恰有一个正零点;(用图像法证明不给分)
恰有一个正零点;(用图像法证明不给分)(2)若函数
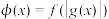 恰有三个零点,求实数
恰有三个零点,求实数 取值范围.
取值范围.
您最近一年使用:0次
2020-11-24更新
|
1259次组卷
|
6卷引用:卷12 指数函数与对数函数 章末复习单元检测(难)-2021-2022学年高一数学单元卷模拟(易中难)(2019人教A版必修第一册)
(已下线)卷12 指数函数与对数函数 章末复习单元检测(难)-2021-2022学年高一数学单元卷模拟(易中难)(2019人教A版必修第一册)(已下线)专题6.2 方程的根与函数零点 B卷-2021-2022学年高一数学单元卷模拟(易中难)(2019人教A版必修第一册)河南省南阳市第一中学校2021-2022学年高一上学期第四次月考数学试题山西省大同市第一中学2021-2022学年高一上学期12 月学情检测数学试题(已下线)专题6.2函数零点与方程根的分布 B卷-2021-2022学年高一数学单元卷模拟(易中难)(人教A版2019必修第一册)广东省深圳市2019-2020学年高一上学期期末数学试题
名校
4 . 若函数 是
是 上的偶函数,
上的偶函数, 是
是 上的奇函数,且满足
上的奇函数,且满足 .
.
(1)求 ,
, 的解析式;
的解析式;
(2)令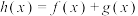 ,证明函数
,证明函数 有且只有
有且只有 个零点.
个零点.
 是
是 上的偶函数,
上的偶函数, 是
是 上的奇函数,且满足
上的奇函数,且满足 .
.(1)求
 ,
, 的解析式;
的解析式;(2)令
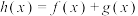 ,证明函数
,证明函数 有且只有
有且只有 个零点.
个零点.
您最近一年使用:0次
2024-06-19更新
|
394次组卷
|
5卷引用:福建省八县(市)一中2020-2021学年高二下学期期末联考数学试题
福建省八县(市)一中2020-2021学年高二下学期期末联考数学试题重庆市清华中学2022届高三上学期7月月考数学试题福建省永泰县第一中学2020-2021学年高二下学期期末数学试题(已下线)专题07函数期末8种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019)(已下线)专题09 导数与零点、不等式综合常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第三册)
5 . 已知函数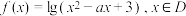 .
.
(1)若 且
且 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(2) ,求解函数的零点,并证明其中大于1的那个零点是无理数;
,求解函数的零点,并证明其中大于1的那个零点是无理数;
(3)若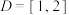 ,且
,且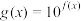 ,设
,设 的最小值为
的最小值为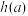 ,求函数
,求函数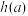 及其定义域
及其定义域 ,并证明其在定义域
,并证明其在定义域 内严格单调递减.
内严格单调递减.
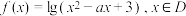 .
.(1)若
 且
且 为偶函数,求实数
为偶函数,求实数 的值;
的值;(2)
 ,求解函数的零点,并证明其中大于1的那个零点是无理数;
,求解函数的零点,并证明其中大于1的那个零点是无理数;(3)若
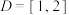 ,且
,且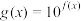 ,设
,设 的最小值为
的最小值为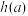 ,求函数
,求函数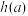 及其定义域
及其定义域 ,并证明其在定义域
,并证明其在定义域 内严格单调递减.
内严格单调递减.
您最近一年使用:0次
解题方法
6 . 设函数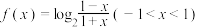 .
.
(1)证明:函数 为奇函数;
为奇函数;
(2)求函数 的零点.
的零点.
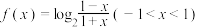 .
.(1)证明:函数
 为奇函数;
为奇函数;(2)求函数
 的零点.
的零点.
您最近一年使用:0次
7 . 已知函数 在定义域
在定义域 上严格单调递增.
上严格单调递增.
(1)证明:函数 至多存在一个零点.
至多存在一个零点.
(2)若函数 存在零点
存在零点 ,证明:存在
,证明:存在 ,使得
,使得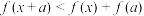 对于任意
对于任意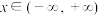 恒成立的充分必要条件是
恒成立的充分必要条件是 .
.
 在定义域
在定义域 上严格单调递增.
上严格单调递增.(1)证明:函数
 至多存在一个零点.
至多存在一个零点.(2)若函数
 存在零点
存在零点 ,证明:存在
,证明:存在 ,使得
,使得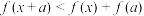 对于任意
对于任意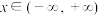 恒成立的充分必要条件是
恒成立的充分必要条件是 .
.
您最近一年使用:0次
解题方法
8 . 已知实系数三次函数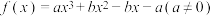 .
.
(1)求证: 是函数
是函数 的零点;
的零点;
(2)a与b满足什么关系时,函数 还有其他零点?
还有其他零点?
(3)如果 是函数
是函数 的零点,求证:
的零点,求证: 也是函数
也是函数 的零点.
的零点.
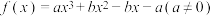 .
.(1)求证:
 是函数
是函数 的零点;
的零点;(2)a与b满足什么关系时,函数
 还有其他零点?
还有其他零点?(3)如果
 是函数
是函数 的零点,求证:
的零点,求证: 也是函数
也是函数 的零点.
的零点.
您最近一年使用:0次
2021-12-02更新
|
136次组卷
|
2卷引用:沪教版(2020) 必修第一册 堂堂清 第五章 5.3(4)函数的应用
9 . 已知函数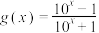 ,
, ,函数
,函数 是函数
是函数 的反函数.
的反函数.
(1)求函数 的解析式,并写出定义域
的解析式,并写出定义域 ;
;
(2)设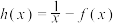 ,判断函数
,判断函数 在区间
在区间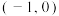 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)设 ,求证:函数
,求证:函数 在区间
在区间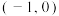 内必有唯一的零点,并求出该零点.(精确到
内必有唯一的零点,并求出该零点.(精确到 ).
).
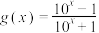 ,
, ,函数
,函数 是函数
是函数 的反函数.
的反函数.(1)求函数
 的解析式,并写出定义域
的解析式,并写出定义域 ;
;(2)设
 ,判断函数
,判断函数 在区间
在区间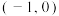 上的单调性,并说明理由;
上的单调性,并说明理由;(3)设
 ,求证:函数
,求证:函数 在区间
在区间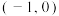 内必有唯一的零点,并求出该零点.(精确到
内必有唯一的零点,并求出该零点.(精确到 ).
).
您最近一年使用:0次
名校
10 . 已知函数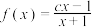 (
( 为常数),若1为函数
为常数),若1为函数 的零点.
的零点.
(1)求 的值;
的值;
(2)证明函数 在
在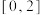 上是单调增函数;
上是单调增函数;
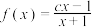 (
( 为常数),若1为函数
为常数),若1为函数 的零点.
的零点.(1)求
 的值;
的值;(2)证明函数
 在
在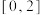 上是单调增函数;
上是单调增函数;
您最近一年使用:0次
2023-02-25更新
|
186次组卷
|
2卷引用:湖北省武汉市第四十九中学2021-2022学年高一上学期期中模拟考试数学试题



