1 . 将数列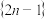 中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列,
中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列,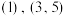 ,
, ,…,则以下结论中正确的是( )
,…,则以下结论中正确的是( )
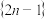 中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列,
中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列,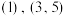 ,
, ,…,则以下结论中正确的是( )
,…,则以下结论中正确的是( )| A.第10个括号内的第一个数为1025 | B.2021在第11个括号内 |
| C.前10个括号内一共有1025个数 | D.第10个括号内的数字之和 |
您最近一年使用:0次
解题方法
2 . 已知新同学小王每天中午会在自己学校提供的A、B两家餐厅中选择就餐,小王第1天午餐时随机选择一家餐厅用餐、如果第1天去A餐厅,那么第2天去A餐厅的概率为0.8;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.4,如此往复.
(1)求小王第2天中午去A餐厅用餐的概率;
(2)求小王第i天中午去B餐厅用餐的概率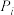 ;
;
(3)已知:若随机变量 服从两点分布,且
服从两点分布,且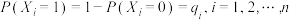 ,则
,则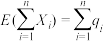 .记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求
.记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求 .
.
(1)求小王第2天中午去A餐厅用餐的概率;
(2)求小王第i天中午去B餐厅用餐的概率
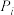 ;
;(3)已知:若随机变量
 服从两点分布,且
服从两点分布,且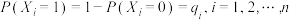 ,则
,则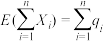 .记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求
.记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求 .
.
您最近一年使用:0次
3 . 若数列 满足:
满足: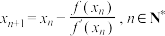 ,则定义数列
,则定义数列 为函数
为函数 的“切线——零点数列”.已知
的“切线——零点数列”.已知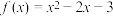 ,数列
,数列 为函数
为函数 的“切线——零底数列”,
的“切线——零底数列”, ,若数列
,若数列 满足
满足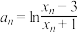 ,则数列
,则数列 的前n项和
的前n项和
___________ .
 满足:
满足: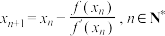 ,则定义数列
,则定义数列 为函数
为函数 的“切线——零点数列”.已知
的“切线——零点数列”.已知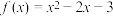 ,数列
,数列 为函数
为函数 的“切线——零底数列”,
的“切线——零底数列”, ,若数列
,若数列 满足
满足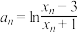 ,则数列
,则数列 的前n项和
的前n项和
您最近一年使用:0次
2024-02-23更新
|
432次组卷
|
4卷引用:福建省福州第三中学2023-2024学年高二上学期1月期末数学试题
福建省福州第三中学2023-2024学年高二上学期1月期末数学试题黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期4月月考数学试题(已下线)模块四 专题5 重组综合练(黑龙江)(8+3+3+5模式)(北师大版高二)(已下线)数学(北京卷03)
解题方法
4 . 已知平面上有 个点
个点 ,
, ,
, ,
, ,
,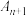 ,
,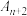 ,
,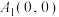 ,
, ,
,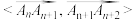
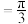 且
且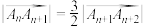 ,记
,记 的坐标为
的坐标为 ,将
,将 ,
,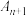 ,
,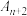 依次顺时针排列,求
依次顺时针排列,求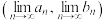 =
=________
 个点
个点 ,
, ,
, ,
, ,
,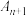 ,
,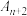 ,
,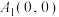 ,
, ,
,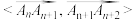
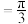 且
且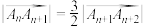 ,记
,记 的坐标为
的坐标为 ,将
,将 ,
,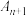 ,
,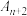 依次顺时针排列,求
依次顺时针排列,求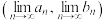 =
=
您最近一年使用:0次
2023-12-16更新
|
390次组卷
|
5卷引用:上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)
(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)上海市嘉定区2024届高三上学期质量调研数学试题上海市普陀区长征中学2024届高三上学期10月月考数学试题(已下线)第4章 数列(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)(已下线)第16题 数列递推求通项(高三二轮每日一题)
5 . 在数列 中,
中, ,
,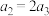 ,且数列
,且数列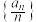 是等比数列.
是等比数列.
(1)求 的通项公式;
的通项公式;
(2)设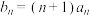 ,数列
,数列 的前n项和为
的前n项和为 ,证明:
,证明: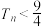 .
.
 中,
中, ,
,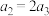 ,且数列
,且数列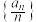 是等比数列.
是等比数列.(1)求
 的通项公式;
的通项公式;(2)设
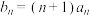 ,数列
,数列 的前n项和为
的前n项和为 ,证明:
,证明: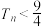 .
.
您最近一年使用:0次
6 . 如图1,抛物线上任意两点连接所得的弦与抛物线围成一个弓形区域,求抛物线弓形区域的面积是古希腊数学家阿基米得最优美的成果之一,阿基米德的计算方法是:将弓形区域分割成无数个三角形,然后将所有三角形的面积加起来就可以得到弓形区域的面积.第一次分割,如图2,在弓形区域里以 为底边分割出一个三角形
为底边分割出一个三角形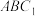 ,确保过顶点
,确保过顶点 的抛物线
的抛物线 的切线与底边
的切线与底边 平行,
平行,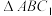 称为一级三角形;第二次分割,如图3,以
称为一级三角形;第二次分割,如图3,以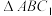 ,两个边
,两个边 ,
, 为底边,在第一次分割得到的两个弓形区域继续分割出两个三角形
为底边,在第一次分割得到的两个弓形区域继续分割出两个三角形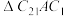 ,
, ,确保过顶点
,确保过顶点 ,
,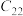 的抛物线
的抛物线 的切线分别与
的切线分别与 ,
, 平行,
平行,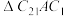 ,
, 都称为二级三角形;重复上述方法,继续分割新产生的弓形区域……,借助抛物线几何性质,阿基米德计算得出任意一级的所有三角形的面积都相等,且每个三角形的面积都是其上一级的一个三角形面积的
都称为二级三角形;重复上述方法,继续分割新产生的弓形区域……,借助抛物线几何性质,阿基米德计算得出任意一级的所有三角形的面积都相等,且每个三角形的面积都是其上一级的一个三角形面积的 .设抛物线
.设抛物线 的方程为
的方程为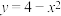 ,直线
,直线 的方程为
的方程为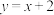 ,请你根据上述阿基米德的计算方法,求经过
,请你根据上述阿基米德的计算方法,求经过 次分割后得到的所有三角形面积之和为
次分割后得到的所有三角形面积之和为__________ .
 为底边分割出一个三角形
为底边分割出一个三角形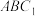 ,确保过顶点
,确保过顶点 的抛物线
的抛物线 的切线与底边
的切线与底边 平行,
平行, 称为一级三角形;第二次分割,如图3,以
称为一级三角形;第二次分割,如图3,以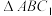 ,两个边
,两个边 ,
, 为底边,在第一次分割得到的两个弓形区域继续分割出两个三角形
为底边,在第一次分割得到的两个弓形区域继续分割出两个三角形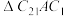 ,
, ,确保过顶点
,确保过顶点 ,
,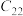 的抛物线
的抛物线 的切线分别与
的切线分别与 ,
, 平行,
平行,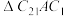 ,
, 都称为二级三角形;重复上述方法,继续分割新产生的弓形区域……,借助抛物线几何性质,阿基米德计算得出任意一级的所有三角形的面积都相等,且每个三角形的面积都是其上一级的一个三角形面积的
都称为二级三角形;重复上述方法,继续分割新产生的弓形区域……,借助抛物线几何性质,阿基米德计算得出任意一级的所有三角形的面积都相等,且每个三角形的面积都是其上一级的一个三角形面积的 .设抛物线
.设抛物线 的方程为
的方程为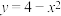 ,直线
,直线 的方程为
的方程为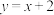 ,请你根据上述阿基米德的计算方法,求经过
,请你根据上述阿基米德的计算方法,求经过 次分割后得到的所有三角形面积之和为
次分割后得到的所有三角形面积之和为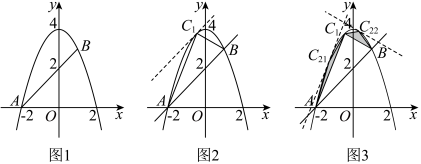
您最近一年使用:0次
7 . 已知 是等差数列,
是等差数列, 是递增的等比数列.
是递增的等比数列.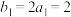 ,
,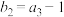 ,
,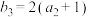 .
.
(1)求数列 和
和 的通项公式及
的通项公式及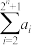 ;
;
(2)若数列 满足
满足 ,
,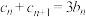 ,
,
(ⅰ)求证: 为等比数列;
为等比数列;
(ⅱ)设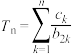 ,对
,对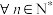 ,都有
,都有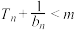 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是等差数列,
是等差数列, 是递增的等比数列.
是递增的等比数列.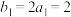 ,
,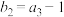 ,
,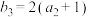 .
.(1)求数列
 和
和 的通项公式及
的通项公式及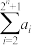 ;
;(2)若数列
 满足
满足 ,
,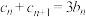 ,
,(ⅰ)求证:
 为等比数列;
为等比数列;(ⅱ)设
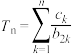 ,对
,对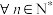 ,都有
,都有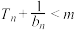 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
22-23高一下·上海浦东新·期末
名校
解题方法
8 . 定义:若对任意正整数n,数列 的前n项和
的前n项和 都为完全平方数,则称数列
都为完全平方数,则称数列 为“完全平方数列”;特别地,若存在正整数n,使得数列
为“完全平方数列”;特别地,若存在正整数n,使得数列 的前n项和
的前n项和 为完全平方数,则称数列
为完全平方数,则称数列 为“部分平方数列”.
为“部分平方数列”.
(1)若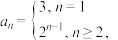
 ,求证:
,求证: 为部分平方数列;
为部分平方数列;
(2)若数列 的前n项和
的前n项和 (t是正整数),那么数列
(t是正整数),那么数列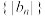 是否为“完全平方数列”?若是,求出t的值;若不是,请说明理由;
是否为“完全平方数列”?若是,求出t的值;若不是,请说明理由;
(3)试求所有为“完全平方数列”的等差数列的通项公式.
 的前n项和
的前n项和 都为完全平方数,则称数列
都为完全平方数,则称数列 为“完全平方数列”;特别地,若存在正整数n,使得数列
为“完全平方数列”;特别地,若存在正整数n,使得数列 的前n项和
的前n项和 为完全平方数,则称数列
为完全平方数,则称数列 为“部分平方数列”.
为“部分平方数列”.(1)若
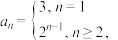
 ,求证:
,求证: 为部分平方数列;
为部分平方数列;(2)若数列
 的前n项和
的前n项和 (t是正整数),那么数列
(t是正整数),那么数列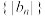 是否为“完全平方数列”?若是,求出t的值;若不是,请说明理由;
是否为“完全平方数列”?若是,求出t的值;若不是,请说明理由;(3)试求所有为“完全平方数列”的等差数列的通项公式.
您最近一年使用:0次
9 . 某高中通过甲、乙两家餐厅给1920名学生提供午餐,通过调查发现:开学后第一天有 的学生到甲餐厅就餐,剩余的学生到乙餐厅就餐,从第二天起,在前一天选择甲餐厅就餐的学生中,次日会有
的学生到甲餐厅就餐,剩余的学生到乙餐厅就餐,从第二天起,在前一天选择甲餐厅就餐的学生中,次日会有 的学生继续选择甲餐厅,在前一天选择乙餐厅就餐的学生中,次日会有
的学生继续选择甲餐厅,在前一天选择乙餐厅就餐的学生中,次日会有 的学生选择甲餐厅.设开学后第
的学生选择甲餐厅.设开学后第 天选择甲餐厅就餐的学生比例为
天选择甲餐厅就餐的学生比例为 ,则( )
,则( )
 的学生到甲餐厅就餐,剩余的学生到乙餐厅就餐,从第二天起,在前一天选择甲餐厅就餐的学生中,次日会有
的学生到甲餐厅就餐,剩余的学生到乙餐厅就餐,从第二天起,在前一天选择甲餐厅就餐的学生中,次日会有 的学生继续选择甲餐厅,在前一天选择乙餐厅就餐的学生中,次日会有
的学生继续选择甲餐厅,在前一天选择乙餐厅就餐的学生中,次日会有 的学生选择甲餐厅.设开学后第
的学生选择甲餐厅.设开学后第 天选择甲餐厅就餐的学生比例为
天选择甲餐厅就餐的学生比例为 ,则( )
,则( )A.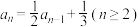 |
B.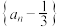 是等比数列 是等比数列 |
C.第100天选择甲餐厅就餐的学生比例约为 |
| D.开学后第一个星期(7天)中在甲餐厅就过餐的有5750人次 |
您最近一年使用:0次
2024-02-11更新
|
355次组卷
|
2卷引用:河南省开封市五校2023-2024学年高二上学期期末联考数学试题
解题方法
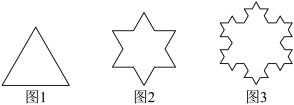
10 . 瑞典数学家科赫在1904年构造能描述雪花形状的图案,就是数学中一朵美丽的雪花——“科赫雪花”.它的绘制规则是:任意画一个正三角形 (图1),并把每一条边三等分,再以中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线
(图1),并把每一条边三等分,再以中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线 (图2),如此继续下去形成雪花曲线
(图2),如此继续下去形成雪花曲线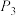 (图3),直到无穷,形成雪花曲线
(图3),直到无穷,形成雪花曲线 .设雪花曲线
.设雪花曲线 的边数为
的边数为 ,面积为
,面积为 ,若正三角形
,若正三角形 的边长为
的边长为 ,则
,则 =
=________ ;  =
=________ .
 (图1),并把每一条边三等分,再以中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线
(图1),并把每一条边三等分,再以中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线 (图2),如此继续下去形成雪花曲线
(图2),如此继续下去形成雪花曲线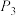 (图3),直到无穷,形成雪花曲线
(图3),直到无穷,形成雪花曲线 .设雪花曲线
.设雪花曲线 的边数为
的边数为 ,面积为
,面积为 ,若正三角形
,若正三角形 的边长为
的边长为 ,则
,则 =
= =
=
您最近一年使用:0次
2024-03-06更新
|
297次组卷
|
2卷引用:福建省福州市八县(市、区)一中2023-2024学年高二上学期期末联考数学试题



