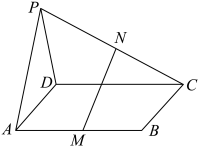
1 . 如图,在三棱锥 中,
中, 底面ABC,
底面ABC,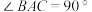 .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,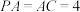 ,
, .
.
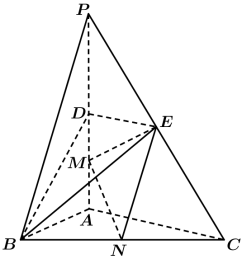
(1)求证: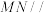 平面BDE;
平面BDE;
(2)求二面角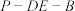 的余弦值.
的余弦值.
 中,
中, 底面ABC,
底面ABC,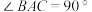 .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,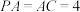 ,
, .
.
(1)求证:
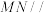 平面BDE;
平面BDE;(2)求二面角
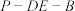 的余弦值.
的余弦值.
您最近一年使用:0次
名校
解题方法
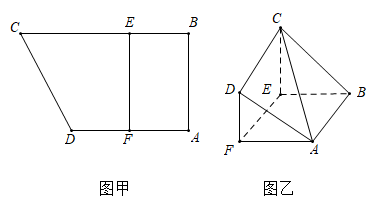
2 . 如图甲,直角梯形 中,
中, ,
, ,
, 为
为 中点,
中点, 在
在 上,且
上,且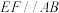 ,已知
,已知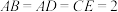 ,现沿
,现沿 把四边形
把四边形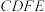 折起(如图乙),使平面
折起(如图乙),使平面 平面
平面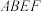 .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
 中,
中, ,
, ,
, 为
为 中点,
中点, 在
在 上,且
上,且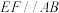 ,已知
,已知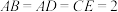 ,现沿
,现沿 把四边形
把四边形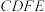 折起(如图乙),使平面
折起(如图乙),使平面 平面
平面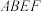 .
.
(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 .
.
您最近一年使用:0次
2022-01-07更新
|
597次组卷
|
3卷引用:广东省佛山市第一中学2021-2022学年高二上学期期中数学试题
解题方法
3 . 已知 是矩形
是矩形 所在平面外一点,
所在平面外一点, ,
, 分别是
分别是 ,
, 的中点,求证:
的中点,求证: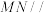 平面
平面 .
.
 是矩形
是矩形 所在平面外一点,
所在平面外一点, ,
, 分别是
分别是 ,
, 的中点,求证:
的中点,求证: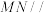 平面
平面 .
.
您最近一年使用:0次
解题方法
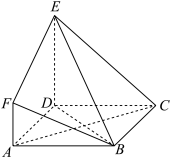
4 . 如图,四边形 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
,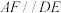 ,
, ,
, 与平面
与平面 所成角为
所成角为 .
.
(1)求证: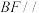 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
,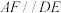 ,
, ,
, 与平面
与平面 所成角为
所成角为 .
.
(1)求证:
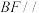 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
名校
解题方法
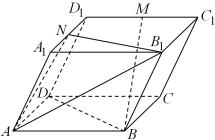
5 . 如图所示的平行六面体 中,已知
中,已知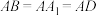 ,
,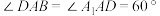 ,
,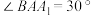 ,
, 为
为 上一点,且
上一点,且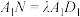 ,点
,点 棱
棱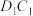 上,且
上,且 .
.
(1)用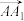 ,
,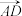 ,
, 表示
表示 ;
;
(2)若 ,求
,求 ;
;
(3)若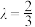 ,求证:
,求证: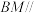 平面
平面 .
.
 中,已知
中,已知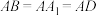 ,
,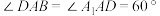 ,
,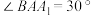 ,
, 为
为 上一点,且
上一点,且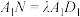 ,点
,点 棱
棱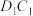 上,且
上,且 .
.
(1)用
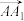 ,
,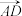 ,
, 表示
表示 ;
;(2)若
 ,求
,求 ;
;(3)若
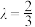 ,求证:
,求证: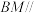 平面
平面 .
.
您最近一年使用:0次
名校
6 . 如图所示,正方形 所在平面与梯形
所在平面与梯形 所在平面垂直,
所在平面垂直,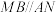 ,
, ,
,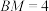 ,
,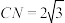
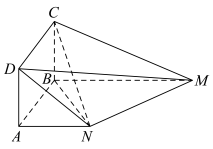
(1)证明: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)在线段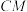 上是否存在一点
上是否存在一点 ,使得平面
,使得平面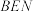 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为 ,若存在求出
,若存在求出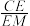 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 所在平面与梯形
所在平面与梯形 所在平面垂直,
所在平面垂直,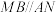 ,
, ,
,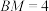 ,
,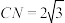

(1)证明:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在线段
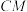 上是否存在一点
上是否存在一点 ,使得平面
,使得平面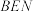 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为 ,若存在求出
,若存在求出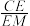 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次
2021-11-22更新
|
446次组卷
|
3卷引用:天津市第四十三中学2021-2022学年高二上学期期中数学试题
解题方法
7 . 如图,平面 平面
平面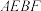 ,四边形
,四边形 为矩形,
为矩形,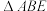 和
和 均为等腰直角三角形,且
均为等腰直角三角形,且 .
.
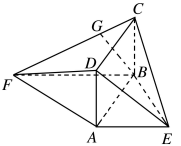
(1)求证:平面 平面
平面 ;
;
(2)若点 为线段
为线段 上任意一点,求证:
上任意一点,求证: 平面
平面 .
.
 平面
平面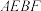 ,四边形
,四边形 为矩形,
为矩形,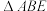 和
和 均为等腰直角三角形,且
均为等腰直角三角形,且 .
.
(1)求证:平面
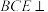 平面
平面 ;
;(2)若点
 为线段
为线段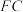 上任意一点,求证:
上任意一点,求证: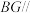 平面
平面 .
.
您最近一年使用:0次
2021-10-27更新
|
647次组卷
|
3卷引用:辽宁省辽东南协作体2021-2022学年高三上学期期中考试数学试题
名校
8 . 在四棱锥 中,
中, 为等边三角形,
为等边三角形,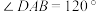 ,
, ,点
,点 为
为 的中点.
的中点.

(1)求证: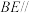 平面
平面 ;
;
(2)已知平面 平面
平面 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,
中, 为等边三角形,
为等边三角形,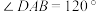 ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:
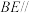 平面
平面 ;
;(2)已知平面
 平面
平面 ,求二面角
,求二面角 的余弦值.
的余弦值.
您最近一年使用:0次
2021-10-09更新
|
1522次组卷
|
5卷引用:河北省保定市唐县第一中学2022-2023学年高三上学期11月期中考试数学试题
名校
解题方法
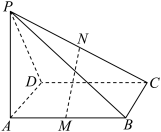
9 . 如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点 平面PAD;
平面PAD;
(2)在PB上确定一个点Q,使平面MNQ 平面PAD.
平面PAD.
 平面PAD;
平面PAD;(2)在PB上确定一个点Q,使平面MNQ
 平面PAD.
平面PAD.
您最近一年使用:0次
2021-09-09更新
|
1630次组卷
|
8卷引用:广东省珠海市艺术高级中学2020-2021学年高一下学期期中数学试题
名校
解题方法
10 . 如图,在直四棱柱 中,底面四边形
中,底面四边形 为梯形,点
为梯形,点 为
为 上一点,且
上一点,且 ,
, ,
, .
.
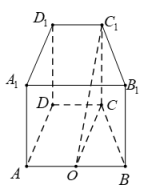
(1)求证: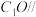 平面
平面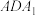 ;
;
(2)求点 到平面
到平面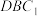 的距离.
的距离.
 中,底面四边形
中,底面四边形 为梯形,点
为梯形,点 为
为 上一点,且
上一点,且 ,
, ,
,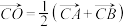 .
.
(1)求证:
 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2021-06-07更新
|
822次组卷
|
6卷引用:山西大学附属中学2022届高三上学期11月期中数学(文)试题
山西大学附属中学2022届高三上学期11月期中数学(文)试题山西省吕梁学院附属高级中学2022届高三上学期期中数学(文)试题安徽省蚌埠市第二中学2021届高三下学期高考最后一模文科数学试题四川省遂宁市2021届高三三模数学(文)试题(已下线)考点32 直线、平面平行的判定及其性质-备战2022年高考数学(文)一轮复习考点帮河南省名校联盟2021-2022学年上学期高三第一次诊断考试文科数学试题



