解题方法
1 . 四棱锥 中,
中, 底面
底面 ,底面
,底面 是正方形,且
是正方形,且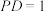 ,
, ,
, 是
是 的重心,则
的重心,则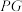 与平面
与平面 所成角
所成角 的正弦值为
的正弦值为______ .
 中,
中, 底面
底面 ,底面
,底面 是正方形,且
是正方形,且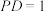 ,
, ,
, 是
是 的重心,则
的重心,则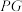 与平面
与平面 所成角
所成角 的正弦值为
的正弦值为
您最近一年使用:0次
2024-10-24更新
|
566次组卷
|
4卷引用:广东省部分学校2024-2025学年高二上学期第一次联考数学试卷
解题方法
2 . 如图,在正方体 中,
中, 为
为 的中点,
的中点,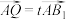 ,
,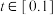 ;当
;当 与
与 所成角的余弦值为
所成角的余弦值为 时,则
时,则
______ .
 中,
中, 为
为 的中点,
的中点,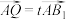 ,
,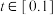 ;当
;当 与
与 所成角的余弦值为
所成角的余弦值为 时,则
时,则

您最近一年使用:0次
名校
解题方法
3 . 两条异面直线 ,
, 所成的角为
所成的角为 ,在直线
,在直线 ,
, 上分别取点
上分别取点 、
、 和点
和点 、
、 ,使得
,使得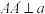 ,且
,且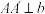 .已知
.已知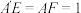 ,
, ,
, ,则
,则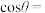
_____ .
 ,
, 所成的角为
所成的角为 ,在直线
,在直线 ,
, 上分别取点
上分别取点 、
、 和点
和点 、
、 ,使得
,使得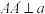 ,且
,且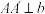 .已知
.已知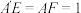 ,
, ,
, ,则
,则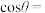
您最近一年使用:0次
名校
解题方法
4 . 空间四边形 中,
中, ,且异面直线
,且异面直线 与
与 成
成 ,求异面直线
,求异面直线 与
与 所成角的余弦值为
所成角的余弦值为______ .
 中,
中, ,且异面直线
,且异面直线 与
与 成
成 ,求异面直线
,求异面直线 与
与 所成角的余弦值为
所成角的余弦值为
您最近一年使用:0次
2024-10-19更新
|
555次组卷
|
2卷引用:广东省梅州市梅县东山中学2024-2025学年高二上学期月考(一) 数学试卷
名校
解题方法
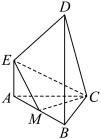
5 . 如图,在多面体 中,
中,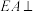 平面
平面 ,
,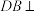 平面
平面 ,
, ,且
,且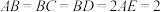 ,M是AB的中点,则平面
,M是AB的中点,则平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为______ .
 中,
中,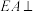 平面
平面 ,
,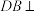 平面
平面 ,
, ,且
,且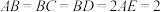 ,M是AB的中点,则平面
,M是AB的中点,则平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为
您最近一年使用:0次
2024-10-13更新
|
552次组卷
|
3卷引用:广东省中山市第一中学2023-2024学年高二上学期第一次段考数学试题
名校
解题方法
6 . 如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,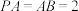 ,
,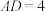 ,
, 为
为 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为_______ .
 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,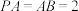 ,
,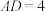 ,
, 为
为 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为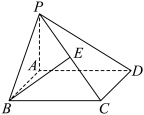
您最近一年使用:0次
2024-09-15更新
|
1002次组卷
|
2卷引用:广东省惠州市第一中学2024-2025学年高二上学期9月阶段考试数学试题
解题方法
7 . 两平面的法向量分别为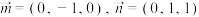 ,则两平面的夹角为
,则两平面的夹角为__________ .
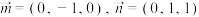 ,则两平面的夹角为
,则两平面的夹角为
您最近一年使用:0次
名校
解题方法
8 . 已知梯形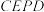 如图1所示,其中
如图1所示,其中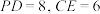 ,A为线段
,A为线段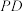 的中点,四边形
的中点,四边形 为正方形,现沿
为正方形,现沿 进行折叠,使得平面
进行折叠,使得平面 ⊥平面
⊥平面 ,得到如图2所示的几何体.已知当点F满足
,得到如图2所示的几何体.已知当点F满足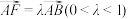 时,平面
时,平面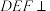 平面
平面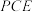 ,则λ的值为
,则λ的值为________ .
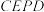 如图1所示,其中
如图1所示,其中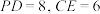 ,A为线段
,A为线段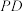 的中点,四边形
的中点,四边形 为正方形,现沿
为正方形,现沿 进行折叠,使得平面
进行折叠,使得平面 ⊥平面
⊥平面 ,得到如图2所示的几何体.已知当点F满足
,得到如图2所示的几何体.已知当点F满足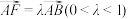 时,平面
时,平面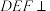 平面
平面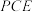 ,则λ的值为
,则λ的值为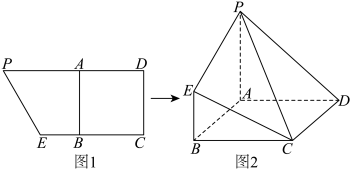
您最近一年使用:0次
2024-09-04更新
|
1121次组卷
|
6卷引用:广东省佛山市南海区罗村高级中学2024-2025学年高二上学期阶段测试一(10月)数学试题
名校
解题方法
9 . 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF 上移动,且CM和BN 的长度保持相等,记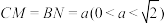 ,当MN的长最小时,平面MNA与平面MNB夹角的正弦值为
,当MN的长最小时,平面MNA与平面MNB夹角的正弦值为_______ .
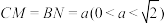 ,当MN的长最小时,平面MNA与平面MNB夹角的正弦值为
,当MN的长最小时,平面MNA与平面MNB夹角的正弦值为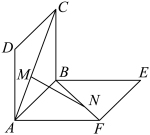
您最近一年使用:0次
2024-08-18更新
|
648次组卷
|
9卷引用:广东省佛山市南海区桂城中学2023-2024学年高二上学期第一次月考数学试卷
广东省佛山市南海区桂城中学2023-2024学年高二上学期第一次月考数学试卷(已下线)微点4 空间向量的应用【练】(高中同步进阶微专题)河南省洛阳市宜阳县部分高中2024-2025学年高二上学期第一次质量检测(9月)数学试题山东省济南市莱芜第一中学2024-2025学年高二上学期第一次阶段性测数学试题山东省泰安市宁阳县第一中学2024-2025学年高二上学期阶段性考试(一)(10月)数学试题山东省滨州市邹平市第二中学2024-2025学年高二上学期10月学业质量检测数学试题四川省南充市嘉陵第一中学2024-2025学年高二上学期第一次月考数学试题山东省肥城市慈明学校2024-2025学年高二上学期第一次月考数学试卷山东省济宁市嘉祥县第一中学2024-2025学年高二上学期第一次月考数学试题
名校
解题方法
10 . 在正方体 中,点P、Q分别在
中,点P、Q分别在 、
、 上,且
上,且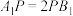 ,
,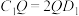 ,则异面直线
,则异面直线 与
与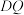 所成角的余弦值为
所成角的余弦值为__________
 中,点P、Q分别在
中,点P、Q分别在 、
、 上,且
上,且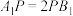 ,
,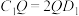 ,则异面直线
,则异面直线 与
与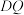 所成角的余弦值为
所成角的余弦值为
您最近一年使用:0次
2024-08-17更新
|
743次组卷
|
3卷引用:2025届广东省三校“决胜高考,梦圆乙巳”第一次联合模拟(一模)考试数学试题
2025届广东省三校“决胜高考,梦圆乙巳”第一次联合模拟(一模)考试数学试题广东省惠州市综合高级中学2024-2025学年高二上学期9月月考数学试卷(B)(已下线)难度4 小题强化限时晋级练(高二期中题型)



