解题方法
1 . 已知圆O: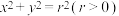 .
.
(1)求证:过圆O上点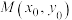 的切线方程为
的切线方程为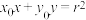 .类比前面的结论,写出过椭圆C:
.类比前面的结论,写出过椭圆C: 上一点
上一点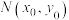 的切线方程(不用证明).
的切线方程(不用证明).
(2)已知椭圆C: ,Q为直线
,Q为直线 上任一点,过点Q作椭圆C的切线,切点分别为A、B,利用(1)的结论,求证:直线AB恒过定点.
上任一点,过点Q作椭圆C的切线,切点分别为A、B,利用(1)的结论,求证:直线AB恒过定点.
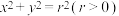 .
.(1)求证:过圆O上点
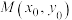 的切线方程为
的切线方程为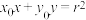 .类比前面的结论,写出过椭圆C:
.类比前面的结论,写出过椭圆C: 上一点
上一点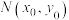 的切线方程(不用证明).
的切线方程(不用证明).(2)已知椭圆C:
 ,Q为直线
,Q为直线 上任一点,过点Q作椭圆C的切线,切点分别为A、B,利用(1)的结论,求证:直线AB恒过定点.
上任一点,过点Q作椭圆C的切线,切点分别为A、B,利用(1)的结论,求证:直线AB恒过定点.
您最近半年使用:0次
2022-02-27更新
|
503次组卷
|
4卷引用:河南省南阳市2021-2022学年高三上学期期末数学(理科)试题
河南省南阳市2021-2022学年高三上学期期末数学(理科)试题河南省南阳市2021-2022学年高三上学期期末数学(理)试题(已下线)技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题36 切线与切点弦问题
2 . (1)若圆 的方程是
的方程是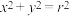 ,求证:过圆
,求证:过圆 上一点
上一点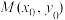 的切线方程为
的切线方程为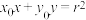 .
.
(2)若圆 的方程是
的方程是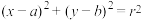 ,则过圆
,则过圆 上一点
上一点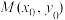 的切线方程为
的切线方程为_______ ,并证明你的结论.
 的方程是
的方程是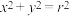 ,求证:过圆
,求证:过圆 上一点
上一点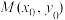 的切线方程为
的切线方程为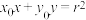 .
.(2)若圆
 的方程是
的方程是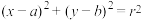 ,则过圆
,则过圆 上一点
上一点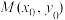 的切线方程为
的切线方程为
您最近半年使用:0次
2020-02-29更新
|
220次组卷
|
2卷引用:上海市七宝中学2019-2020学年高二上学期期末数学试题
解题方法
3 . 如图,P是直线 上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过
上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过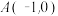 作圆Γ的两条切线分别与l交于E,F两点.
作圆Γ的两条切线分别与l交于E,F两点.
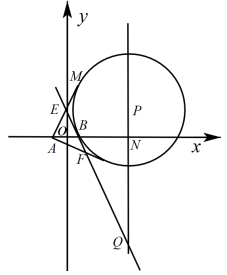
(1) 求证: 为定值
为定值
(2)设直线l交直线 于点Q,证明:
于点Q,证明:
 上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过
上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过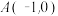 作圆Γ的两条切线分别与l交于E,F两点.
作圆Γ的两条切线分别与l交于E,F两点.
(1) 求证:
 为定值
为定值(2)设直线l交直线
 于点Q,证明:
于点Q,证明:
您最近半年使用:0次
2017-08-08更新
|
1154次组卷
|
2卷引用:浙江省杭州市2016-2017学年高二下学期期末教学质量检测数学试题
名校
4 . 在平面直角坐标系中,点 在抛物线
在抛物线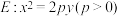 上.
上.
(1)求
 的准线方程.
的准线方程.(2)已知点
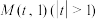 ,
, ,
, 是
是 的两条切线,
的两条切线, ,
, 是切点,圆
是切点,圆 经过点
经过点 ,
, ,
, .
.①若 ,求证:
,求证: ;
;
②设圆 在
在 ,
, 处的切线的交点为
处的切线的交点为 ,求证:直线
,求证:直线 过定点.
过定点.
附:若点
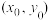 在圆
在圆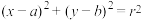 上,则圆在点
上,则圆在点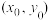 处的切线方程为
处的切线方程为 .
.
您最近半年使用:0次
解题方法
5 . 已知圆C: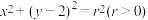 和直线l:
和直线l: 相切.
相切.
(1)求圆C半径 ;
;
(2)若动点M在直线 上,过点M引圆C的两条切线MA、MB,切点分别为A、B.
上,过点M引圆C的两条切线MA、MB,切点分别为A、B.
①记四边形MACB的面积为S,求S的最小值;
②证明直线AB恒过定点.
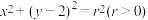 和直线l:
和直线l: 相切.
相切.(1)求圆C半径
 ;
;(2)若动点M在直线
 上,过点M引圆C的两条切线MA、MB,切点分别为A、B.
上,过点M引圆C的两条切线MA、MB,切点分别为A、B.①记四边形MACB的面积为S,求S的最小值;
②证明直线AB恒过定点.
您最近半年使用:0次
名校
解题方法
6 . 已知圆 ,点P为直线
,点P为直线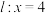 上的动点.
上的动点.
(1)若从P到圆O的切线长为 ,求P点的坐标以及两条切线所夹劣弧长;
,求P点的坐标以及两条切线所夹劣弧长;
(2)若点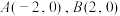 ,直线
,直线 与圆O的另一个交点分别为
与圆O的另一个交点分别为 ,求证:直线
,求证:直线 经过定点
经过定点 .
.
 ,点P为直线
,点P为直线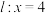 上的动点.
上的动点.(1)若从P到圆O的切线长为
 ,求P点的坐标以及两条切线所夹劣弧长;
,求P点的坐标以及两条切线所夹劣弧长;(2)若点
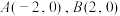 ,直线
,直线 与圆O的另一个交点分别为
与圆O的另一个交点分别为 ,求证:直线
,求证:直线 经过定点
经过定点 .
.
您最近半年使用:0次
2024-01-14更新
|
147次组卷
|
21卷引用:2015届江西省吉安市一中高三上学期期中考试理科数学试卷
2015届江西省吉安市一中高三上学期期中考试理科数学试卷2015届江西省吉安市一中高三上学期期中考试文科数学试卷苏教版(2019) 选修第一册 突围者 第2章 专项拓展训练2 与圆有关的定点、定值、探索性问题北师大版(2019) 选修第一册 突围者 第一章 专项拓展训练2 与圆有关的对称问题、最值问题黑龙江省哈尔滨市第三中学2021-2022学年高二上学期10月月考数学(普通班)试题湖南省长沙市长郡中学2021-2022学年高二上学期第一次月考数学试题人教B版(2019) 选修第一册 学习帮手 第二章 2.3.3 直线与圆的位置关系(第一课时)江苏省苏州市星海实验中学2021-2022学年高二上学期10月学情调研数学试题苏教版(2019) 选修第一册 一蹴而就 第2章 微专题集训二 圆的综合问题2023版 北师大版(2019) 选修第一册 突围者 第一章 专项拓展训练3 与圆有关的定点、定值、探索性问题湖南省长沙市长郡湘府中学2022-2023学年高二上学期第一次月考数学试题江西省赣州市赣县第三中学2022-2023学年高二上学期9月月考数学试题福建省厦门第二中学2022-2023学年高二上学期第一阶段考试数学试题第一章 直线和圆 单元检测卷-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册第一章 直线和圆单元检测B卷(综合篇)福建省漳州市第三中学2022-2023学年高二上学期期中数学试题(已下线)第09讲 直线与圆的位置关系(4大考点)-2022-2023学年高二数学考试满分全攻略(人教A版2019选择性必修第一册)(已下线)第二章 直线与圆的方程(压轴必刷30题5种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期中真题必刷压轴60题(18个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)江西省上饶市广丰区大千艺术学校2023-2024学年高二上学期期末数学试题河北省保定市部分学校2023-2024学年高一下学期1+3期中考试数学试题
解题方法
7 . 抛物线 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长.
的短轴长.
(1)求抛物线 的方程;
的方程;
(2)设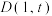 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作
作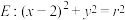 (其中
(其中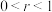 )的两条切线,分别交抛物线
)的两条切线,分别交抛物线 于点
于点 ,过原点作直线
,过原点作直线 的垂线,垂足为
的垂线,垂足为 ,证明点
,证明点 在定圆上,并求定圆方程
在定圆上,并求定圆方程
 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长.
的短轴长.(1)求抛物线
 的方程;
的方程;(2)设
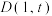 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作
作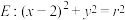 (其中
(其中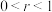 )的两条切线,分别交抛物线
)的两条切线,分别交抛物线 于点
于点 ,过原点作直线
,过原点作直线 的垂线,垂足为
的垂线,垂足为 ,证明点
,证明点 在定圆上,并求定圆方程
在定圆上,并求定圆方程
您最近半年使用:0次
解题方法
8 . 已知圆 过点
过点 ,圆心
,圆心 在直线
在直线 上,且圆
上,且圆 与
与 轴相切.
轴相切.
(1)求圆 的方程;
的方程;
(2)已知圆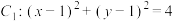 与圆
与圆 交于
交于 、
、 两点,过直线
两点,过直线 上(除线段
上(除线段 部分)一点
部分)一点 分别作两圆的切线,切点分别为点
分别作两圆的切线,切点分别为点 、
、 ,求证:
,求证: .
.
 过点
过点 ,圆心
,圆心 在直线
在直线 上,且圆
上,且圆 与
与 轴相切.
轴相切.(1)求圆
 的方程;
的方程;(2)已知圆
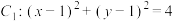 与圆
与圆 交于
交于 、
、 两点,过直线
两点,过直线 上(除线段
上(除线段 部分)一点
部分)一点 分别作两圆的切线,切点分别为点
分别作两圆的切线,切点分别为点 、
、 ,求证:
,求证: .
.
您最近半年使用:0次
解题方法
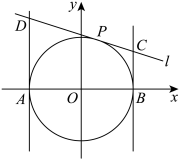
9 . 如图,在平面直角坐标系 中,过
中,过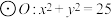 上的点
上的点 作切线
作切线 ,
, 分别与直线
分别与直线 ,
, 交于点
交于点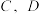 ,圆
,圆 与
与 轴交于点
轴交于点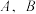 .
.
(1)若 点坐标是
点坐标是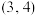 ,求直线
,求直线 的方程;
的方程;
(2)若 是圆
是圆 上的动点,证明:两条动直线
上的动点,证明:两条动直线 的交点
的交点 总在同一个椭圆
总在同一个椭圆 上,并求出椭圆
上,并求出椭圆 的方程.
的方程.
 中,过
中,过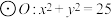 上的点
上的点 作切线
作切线 ,
, 分别与直线
分别与直线 ,
, 交于点
交于点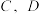 ,圆
,圆 与
与 轴交于点
轴交于点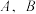 .
.
(1)若
 点坐标是
点坐标是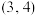 ,求直线
,求直线 的方程;
的方程;(2)若
 是圆
是圆 上的动点,证明:两条动直线
上的动点,证明:两条动直线 的交点
的交点 总在同一个椭圆
总在同一个椭圆 上,并求出椭圆
上,并求出椭圆 的方程.
的方程.
您最近半年使用:0次
2024-02-23更新
|
85次组卷
|
2卷引用:中原名校2022年高三上学期第一次精英联赛文科数学试题
10 . 已知椭圆 ,其离心率为
,其离心率为 ,直线
,直线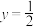 被椭圆截得的弦长为
被椭圆截得的弦长为 .
.
(1)求椭圆 的标准方程.
的标准方程.
(2)圆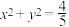 的切线交椭圆
的切线交椭圆 于
于 ,
, 两点,切点为
两点,切点为 ,求证:
,求证: 是定值.
是定值.
 ,其离心率为
,其离心率为 ,直线
,直线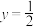 被椭圆截得的弦长为
被椭圆截得的弦长为 .
.(1)求椭圆
 的标准方程.
的标准方程.(2)圆
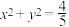 的切线交椭圆
的切线交椭圆 于
于 ,
, 两点,切点为
两点,切点为 ,求证:
,求证: 是定值.
是定值.
您最近半年使用:0次



