解题方法
1 . 设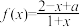 (a为实常数),
(a为实常数),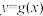 与
与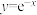 的图像关于y轴对称.
的图像关于y轴对称.
(1)若函数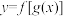 为奇函数,求a的取值;
为奇函数,求a的取值;
(2)当a=0时,若关于x的方程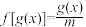 有两个不等实根,求m的范围;
有两个不等实根,求m的范围;
(3)当|a|<1时,求方程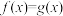 的实数根个数,并加以证明.
的实数根个数,并加以证明.
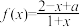 (a为实常数),
(a为实常数),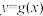 与
与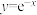 的图像关于y轴对称.
的图像关于y轴对称.(1)若函数
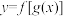 为奇函数,求a的取值;
为奇函数,求a的取值;(2)当a=0时,若关于x的方程
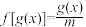 有两个不等实根,求m的范围;
有两个不等实根,求m的范围;(3)当|a|<1时,求方程
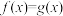 的实数根个数,并加以证明.
的实数根个数,并加以证明.
您最近一年使用:0次
名校
2 . 已知函数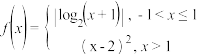 , 若
, 若 有四个互不相等的实数根
有四个互不相等的实数根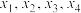 ,且
,且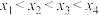 . 则
. 则 的取值
的取值 范围是( ).
范围是( ).
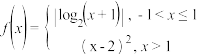 , 若
, 若 有四个互不相等的实数根
有四个互不相等的实数根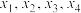 ,且
,且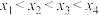 . 则
. 则 的取值
的取值 范围是( ).
范围是( ).A.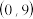 | B.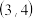 | C. | D.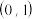 |
您最近一年使用:0次
2019-01-15更新
|
750次组卷
|
3卷引用:四川省宜宾第三中学2018-2019学年高一11月月考数学试题
名校
解题方法
3 . 若关于x的不等式 的解集为
的解集为 ,则实数a的范围是
,则实数a的范围是______ .
 的解集为
的解集为 ,则实数a的范围是
,则实数a的范围是
您最近一年使用:0次
2022-12-24更新
|
609次组卷
|
3卷引用:上海市进才中学2022-2023学年高一上学期12月月考数学试题
上海市进才中学2022-2023学年高一上学期12月月考数学试题(已下线)5.2.3 函数的最值-同步精品课堂(沪教版2020必修第一册)上海市闵行(文绮)中学2023-2024学年高一上学期12月学情调研数学试题
名校
解题方法
4 . 下列命题中正确的是( )
A.已知函数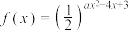 ,若函数 ,若函数 在区间 在区间 上是增函数,则 上是增函数,则 的取值范围是 的取值范围是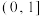 |
B.已知定义在 上的偶函数 上的偶函数 在 在 上单调递增,且 上单调递增,且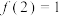 ,若 ,若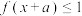 对 对 恒成立,则实数 恒成立,则实数 的取值范围是 的取值范围是 |
C.函数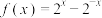 ,若不等式 ,若不等式 对 对 恒成立,则 恒成立,则 范围为 范围为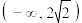 . . |
D.函数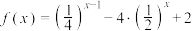 在 在 上的值域为 上的值域为 |
您最近一年使用:0次
23-24高一上·上海浦东新·阶段练习
名校
5 . 已知函数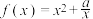 (
(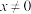 ,常数
,常数 ).
).
(1)求函数 的零点;
的零点;
(2)根据 的不同取值,判断函数
的不同取值,判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围,证明函数
的取值范围,证明函数 在
在 上有且仅有1个零点.
上有且仅有1个零点.
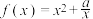 (
(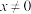 ,常数
,常数 ).
).(1)求函数
 的零点;
的零点;(2)根据
 的不同取值,判断函数
的不同取值,判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)若函数
 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围,证明函数
的取值范围,证明函数 在
在 上有且仅有1个零点.
上有且仅有1个零点.
您最近一年使用:0次
名校
解题方法
6 . 已知函数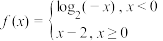 ,若函数
,若函数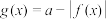 有四个零点
有四个零点 ,
, ,
, ,
, ,且
,且 ,则下列正确的是( )
,则下列正确的是( )
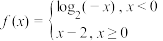 ,若函数
,若函数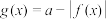 有四个零点
有四个零点 ,
, ,
, ,
, ,且
,且 ,则下列正确的是( )
,则下列正确的是( )A. 的范围 的范围 | B. + + + + + + 的范围 的范围 |
C.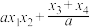 的取值范围 的取值范围  | D. 的范围 的范围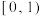 |
您最近一年使用:0次
2023-01-11更新
|
1068次组卷
|
4卷引用:安徽省淮北市第一中学2022-2023学年高一上学期期末数学试题
名校
7 . 给出下列四个命题:①命题“ ”为真,则实数
”为真,则实数 的范围是
的范围是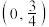 ;②设
;②设 ,则“
,则“ ”是“
”是“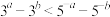 ”的充要条件;③关于
”的充要条件;③关于 的方程
的方程 ,存在实数
,存在实数 ,使得方程恰有5个不同的实根;④函数
,使得方程恰有5个不同的实根;④函数 的定义域为D,若满足:(1)
的定义域为D,若满足:(1) 在D内是单调函数;(2)存在
在D内是单调函数;(2)存在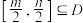 ,使得
,使得 在
在 上的值域为
上的值域为 ,那么就称函数
,那么就称函数 为“梦想函数”.若函数
为“梦想函数”.若函数 是“梦想函数”,则t的取值范围是
是“梦想函数”,则t的取值范围是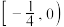 ;其中真命题有
;其中真命题有_________ (填序号)
 ”为真,则实数
”为真,则实数 的范围是
的范围是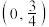 ;②设
;②设 ,则“
,则“ ”是“
”是“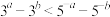 ”的充要条件;③关于
”的充要条件;③关于 的方程
的方程 ,存在实数
,存在实数 ,使得方程恰有5个不同的实根;④函数
,使得方程恰有5个不同的实根;④函数 的定义域为D,若满足:(1)
的定义域为D,若满足:(1) 在D内是单调函数;(2)存在
在D内是单调函数;(2)存在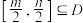 ,使得
,使得 在
在 上的值域为
上的值域为 ,那么就称函数
,那么就称函数 为“梦想函数”.若函数
为“梦想函数”.若函数 是“梦想函数”,则t的取值范围是
是“梦想函数”,则t的取值范围是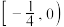 ;其中真命题有
;其中真命题有
您最近一年使用:0次
名校
8 . 已知函数 ,
, .
.
(1)若 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得函数
,使得函数 与函数
与函数 的图象在区间
的图象在区间 上有唯一的交点,若存在,求出
上有唯一的交点,若存在,求出 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
 ,
, .
.(1)若
 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围;
的取值范围;(2)在(1)的条件下,是否存在实数
 ,使得函数
,使得函数 与函数
与函数 的图象在区间
的图象在区间 上有唯一的交点,若存在,求出
上有唯一的交点,若存在,求出 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
您最近一年使用:0次
2022-02-17更新
|
606次组卷
|
4卷引用:广东省茂名市化州市第一中学2021-2022学年高一下学期期中数学试题
名校
9 . 设 ,函数
,函数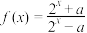 .
.
(1)若 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;
(2)若 ,函数
,函数 在区间
在区间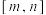 (
( )上的取值范围是
)上的取值范围是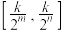 (
(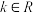 ),求
),求 的范围.
的范围.
 ,函数
,函数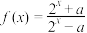 .
.(1)若
 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;(2)若
 ,函数
,函数 在区间
在区间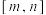 (
( )上的取值范围是
)上的取值范围是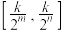 (
(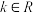 ),求
),求 的范围.
的范围.
您最近一年使用:0次
2022-02-16更新
|
792次组卷
|
4卷引用:广东省广州市天河区2021-2022学年高一上学期期末数学试题
10 . 设 ,函数
,函数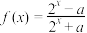 .
.
(1)若 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;
(2)若 ,函数
,函数 在区间
在区间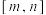
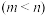 上的取值范围是
上的取值范围是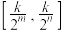
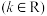 ,求
,求 的范围.
的范围.
 ,函数
,函数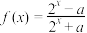 .
.(1)若
 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;(2)若
 ,函数
,函数 在区间
在区间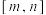
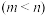 上的取值范围是
上的取值范围是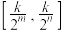
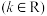 ,求
,求 的范围.
的范围.
您最近一年使用:0次
2022-01-21更新
|
687次组卷
|
2卷引用:浙江省杭州市八县区2021-2022学年高一上学期期末学业水平测试数学试题



