名校
1 . 设 为正整数,集合
为正整数,集合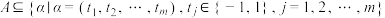 . 任取集合A中的
. 任取集合A中的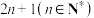 个元素(可以重复)
个元素(可以重复)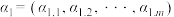 ,
,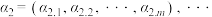 ,
, ,
,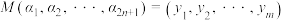 ,其中
,其中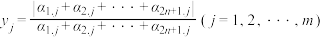 .
.
(1)若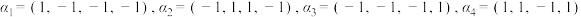 ,
, ,直接写出
,直接写出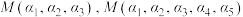 ;
;
(2)对于 ,
, ,
, ,证明:
,证明: ;
;
(3)对于某个正整数 ,若集合A满足:对于A中任意
,若集合A满足:对于A中任意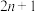 个元素
个元素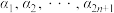 ,都有
,都有 ,则称集合A具有性质
,则称集合A具有性质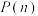 . 证明:若
. 证明:若 ,集合A具有性质
,集合A具有性质 ,则
,则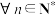 ,集合A都具有性质
,集合A都具有性质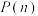 .
.
 为正整数,集合
为正整数,集合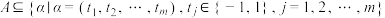 . 任取集合A中的
. 任取集合A中的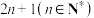 个元素(可以重复)
个元素(可以重复)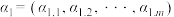 ,
,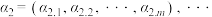 ,
, ,
,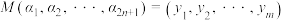 ,其中
,其中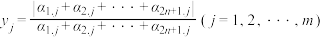 .
.(1)若
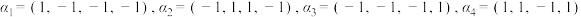 ,
, ,直接写出
,直接写出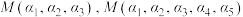 ;
;(2)对于
 ,
, ,
, ,证明:
,证明: ;
;(3)对于某个正整数
 ,若集合A满足:对于A中任意
,若集合A满足:对于A中任意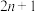 个元素
个元素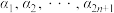 ,都有
,都有 ,则称集合A具有性质
,则称集合A具有性质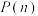 . 证明:若
. 证明:若 ,集合A具有性质
,集合A具有性质 ,则
,则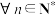 ,集合A都具有性质
,集合A都具有性质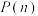 .
.
您最近一年使用:0次
名校
解题方法
2 . 设定义在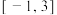 函数
函数 当
当 时,
时, 的值域为
的值域为_______ ;若 的最大值为1,则实数
的最大值为1,则实数 的所有取值组成的集合为
的所有取值组成的集合为______ .
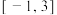 函数
函数 当
当 时,
时, 的值域为
的值域为 的最大值为1,则实数
的最大值为1,则实数 的所有取值组成的集合为
的所有取值组成的集合为
您最近一年使用:0次
23-24高三上·北京西城·期末
解题方法
3 . 设 ,函数
,函数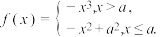 给出下列四个结论:
给出下列四个结论:
① 在区间
在区间 上单调递减;
上单调递减;
②当 时,
时, 存在最大值;
存在最大值;
③当 时,直线
时,直线 与曲线
与曲线 恰有3个交点;
恰有3个交点;
④存在正数 及点
及点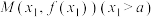 和
和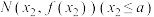 ,使
,使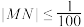 .
.
其中所有正确结论的序号是______ .
 ,函数
,函数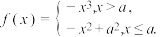 给出下列四个结论:
给出下列四个结论:①
 在区间
在区间 上单调递减;
上单调递减;②当
 时,
时, 存在最大值;
存在最大值;③当
 时,直线
时,直线 与曲线
与曲线 恰有3个交点;
恰有3个交点;④存在正数
 及点
及点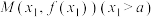 和
和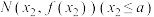 ,使
,使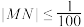 .
.其中所有正确结论的序号是
您最近一年使用:0次
23-24高三上·北京丰台·期末
4 . 已知函数 ,当
,当 时,记函数
时,记函数 的最大值为
的最大值为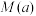 ,则
,则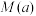 的最小值为( )
的最小值为( )
 ,当
,当 时,记函数
时,记函数 的最大值为
的最大值为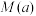 ,则
,则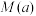 的最小值为( )
的最小值为( )| A.3.5 | B.4 |
| C.4.5 | D.5 |
您最近一年使用:0次
名校
5 . 已知集合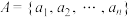 ,其中
,其中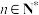 且
且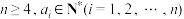 ,非空集合
,非空集合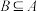 ,记
,记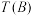 为集合B中所有元素之和,并规定当
为集合B中所有元素之和,并规定当 中只有一个元素
中只有一个元素 时,
时,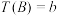 .
.
(1)若 ,写出所有可能的集合B;
,写出所有可能的集合B;
(2)若 ,且
,且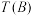 是12的倍数,求集合B的个数;
是12的倍数,求集合B的个数;
(3)若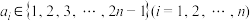 ,证明:存在非空集合
,证明:存在非空集合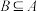 ,使得
,使得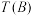 是
是 的倍数.
的倍数.
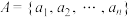 ,其中
,其中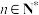 且
且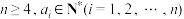 ,非空集合
,非空集合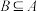 ,记
,记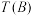 为集合B中所有元素之和,并规定当
为集合B中所有元素之和,并规定当 中只有一个元素
中只有一个元素 时,
时,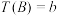 .
.(1)若
 ,写出所有可能的集合B;
,写出所有可能的集合B;(2)若
 ,且
,且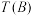 是12的倍数,求集合B的个数;
是12的倍数,求集合B的个数;(3)若
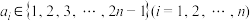 ,证明:存在非空集合
,证明:存在非空集合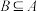 ,使得
,使得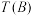 是
是 的倍数.
的倍数.
您最近一年使用:0次
2024-01-20更新
|
275次组卷
|
2卷引用:北京市北师大附中平谷第一分校2023-2024学年高一下学期2月开学测试数学试题
名校
6 . 设 ,已知由自然数组成的集合
,已知由自然数组成的集合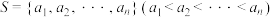 ,集合
,集合 ,
, ,…,
,…, 是
是 的互不相同的非空子集,定义
的互不相同的非空子集,定义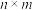 数表:
数表:
 ,其中
,其中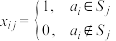 ,设
,设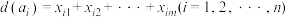 ,令
,令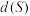 是
是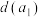 ,
,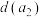 ,…,
,…,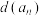 中的最大值.
中的最大值.
(1)若 ,
, ,且
,且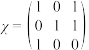 ,求
,求 ,
, ,
, 及
及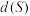 ;
;
(2)若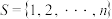 ,集合
,集合 ,
, ,…,
,…, 中的元素个数均相同,若
中的元素个数均相同,若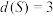 ,求
,求 的最小值;
的最小值;
(3)若 ,
, ,集合
,集合 ,
, ,…,
,…,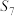 中的元素个数均为3,且
中的元素个数均为3,且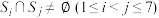 ,求证:
,求证: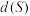 的最小值为3.
的最小值为3.
 ,已知由自然数组成的集合
,已知由自然数组成的集合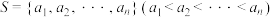 ,集合
,集合 ,
, ,…,
,…, 是
是 的互不相同的非空子集,定义
的互不相同的非空子集,定义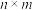 数表:
数表: ,其中
,其中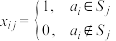 ,设
,设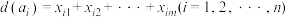 ,令
,令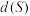 是
是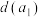 ,
,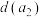 ,…,
,…,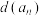 中的最大值.
中的最大值.(1)若
 ,
, ,且
,且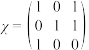 ,求
,求 ,
, ,
, 及
及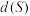 ;
;(2)若
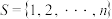 ,集合
,集合 ,
, ,…,
,…, 中的元素个数均相同,若
中的元素个数均相同,若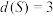 ,求
,求 的最小值;
的最小值;(3)若
 ,
, ,集合
,集合 ,
, ,…,
,…,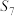 中的元素个数均为3,且
中的元素个数均为3,且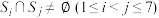 ,求证:
,求证: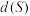 的最小值为3.
的最小值为3.
您最近一年使用:0次
2023-07-10更新
|
524次组卷
|
4卷引用:北京市陈经纶中学2023-2024学年高二上学期开学检测数学试题
北京市陈经纶中学2023-2024学年高二上学期开学检测数学试题北京市朝阳区2022-2023学年高一下学期期末质量检测数学试题(已下线)难关必刷01集合的综合问题(3种题型40题专项训练)-【满分全攻略】(人教A版2019必修第一册)(已下线)高一上学期期末考试解答题压轴题50题专练-举一反三系列
7 . 对任意正整数n,记集合 ,
, .
.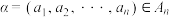 ,
,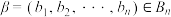 ,若对任意
,若对任意 都有
都有 ,则记
,则记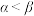 .
.
(1)写出集合 和
和 ;
;
(2)证明:对任意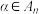 ,存在
,存在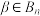 ,使得
,使得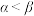 ;
;
(3)设集合 .求证:
.求证: 中的元素个数是完全平方数.
中的元素个数是完全平方数.
 ,
, .
.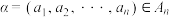 ,
,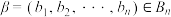 ,若对任意
,若对任意 都有
都有 ,则记
,则记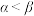 .
.(1)写出集合
 和
和 ;
;(2)证明:对任意
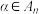 ,存在
,存在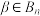 ,使得
,使得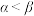 ;
;(3)设集合
 .求证:
.求证: 中的元素个数是完全平方数.
中的元素个数是完全平方数.
您最近一年使用:0次
2023-11-15更新
|
129次组卷
|
4卷引用:北京市第八十中学2023届高三上学期开学考试数学试题
名校
8 . 设函数 的定义域为D,若存在实数
的定义域为D,若存在实数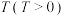 ,使得对于任意
,使得对于任意 ,都有
,都有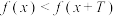 ,则称
,则称 为“
为“ 严格增函数”,对于“
严格增函数”,对于“ 严格增函数”,有以下四个结论:
严格增函数”,有以下四个结论:
①“ 严格增函数”
严格增函数” 一定在D上严格增;
一定在D上严格增;
②“ 严格增函数”
严格增函数” 一定是“
一定是“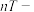 严格增函数”(其中
严格增函数”(其中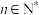 ,且
,且 )
)
③函数 是“
是“ 严格增函数”(其中
严格增函数”(其中 表示不大于x的最大整数)
表示不大于x的最大整数)
④函数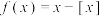 不是“
不是“ 严格增函数”(其中
严格增函数”(其中 表示不大于x的最大整数)
表示不大于x的最大整数)
其中,所有正确的结论序号是______ .
 的定义域为D,若存在实数
的定义域为D,若存在实数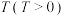 ,使得对于任意
,使得对于任意 ,都有
,都有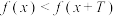 ,则称
,则称 为“
为“ 严格增函数”,对于“
严格增函数”,对于“ 严格增函数”,有以下四个结论:
严格增函数”,有以下四个结论:①“
 严格增函数”
严格增函数” 一定在D上严格增;
一定在D上严格增;②“
 严格增函数”
严格增函数” 一定是“
一定是“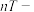 严格增函数”(其中
严格增函数”(其中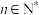 ,且
,且 )
)③函数
 是“
是“ 严格增函数”(其中
严格增函数”(其中 表示不大于x的最大整数)
表示不大于x的最大整数)④函数
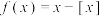 不是“
不是“ 严格增函数”(其中
严格增函数”(其中 表示不大于x的最大整数)
表示不大于x的最大整数)其中,所有正确的结论序号是
您最近一年使用:0次
2022-12-21更新
|
537次组卷
|
3卷引用:北京市海淀区首都师范大学附属中学2023届高三下学期2月阶段性质量检测数学试题
名校
解题方法
9 . 已知定义在R上的函数 满足
满足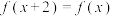 ,当
,当 时,
时,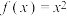 ,函数
,函数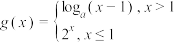 ,若函数
,若函数 在区间
在区间 上恰有8个零点,则a的取值范围为( )
上恰有8个零点,则a的取值范围为( )
 满足
满足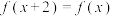 ,当
,当 时,
时,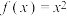 ,函数
,函数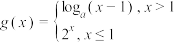 ,若函数
,若函数 在区间
在区间 上恰有8个零点,则a的取值范围为( )
上恰有8个零点,则a的取值范围为( )| A.(2,4) | B.(2,5) | C.(1,5) | D.(1,4) |
您最近一年使用:0次
2022-07-28更新
|
2400次组卷
|
7卷引用:北京市第八十中学2023届高三上学期开学考试数学试题
名校
10 . 已知函数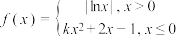 ,给出下列命题:
,给出下列命题:
(1)无论 取何值,
取何值, 恒有两个零点;
恒有两个零点;
(2)存在实数 ,使得
,使得 的值域是
的值域是 ;
;
(3)存在实数 使得
使得 的图像上关于原点对称的点有两对;
的图像上关于原点对称的点有两对;
(4)当 时,若
时,若 的图象与直线
的图象与直线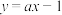 有且只有三个公共点,则实数
有且只有三个公共点,则实数 的取值范围是
的取值范围是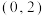 .
.
其中,所有正确命题的序号是___________ .
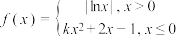 ,给出下列命题:
,给出下列命题:(1)无论
 取何值,
取何值, 恒有两个零点;
恒有两个零点;(2)存在实数
 ,使得
,使得 的值域是
的值域是 ;
;(3)存在实数
 使得
使得 的图像上关于原点对称的点有两对;
的图像上关于原点对称的点有两对;(4)当
 时,若
时,若 的图象与直线
的图象与直线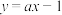 有且只有三个公共点,则实数
有且只有三个公共点,则实数 的取值范围是
的取值范围是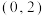 .
.其中,所有正确命题的序号是
您最近一年使用:0次
2022-05-01更新
|
892次组卷
|
3卷引用:北京市第五十七中学2023届高三上学期开学考试数学试题



