9-10高三·广西·阶段练习
1 . 记函数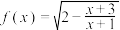 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 .
.
(1)求 ;
;
(2)若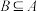 ,求实数
,求实数 的取值范围.
的取值范围.
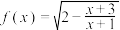 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 .
.(1)求
 ;
;(2)若
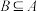 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-26更新
|
874次组卷
|
35卷引用:2015-2016学年河南省信阳高中高一下学期开学考试数学卷
2015-2016学年河南省信阳高中高一下学期开学考试数学卷(已下线)2012届河南省信阳市高中毕业班第一次调研考试文科数学试卷2015-2016学年江西省鹰潭市一中高一11月月考数学试卷河南省灵宝市实验高级中学2017-2018学年度高二下学期第二次月清数学(理)试题【全国百强校】河南省信阳高级中学2018-2019学年高一上学期期末考试数学试题(已下线)2011届广西希望高中高三第一次月考理科数学卷(已下线)2011届内蒙古包头市蒙中高三上学期期中考试数学试卷(已下线)2010--2011学年度北京五中高二第二学期期末考试文科数学(已下线)2012届甘肃省兰州一中高三9月月考试卷文科数学(已下线)2011-2012学年重庆市西南大学附属中学高一上学期期末考试数学(已下线)2012-2013年辽宁朝阳柳城高中高三上第三次月考文科数学试卷(已下线)2012-2013年辽宁朝阳柳城高中高三上第三次月考理科数学试卷(已下线)2013届辽宁省抚顺一中高三9月月考理科数学试卷河北省武邑中学2018届高三上学期第一次月考数学(理)试题(已下线)2018年高考二轮复习测试专项【苏教版】专题一 集合与简易逻辑(已下线)第3章 章末检测-2018-2019版数学创新设计课堂讲义同步系列(苏教版必修5)【全国百强校】江苏省扬州中学2018-2019学年高二4月月考数学(文)试题智能测评与辅导[文]-集合的概念与运算智能测评与辅导[文]-算法、推理与证明(复数)智能测评与辅导[理]-集合的概念与运算山西省朔州市怀仁市重点中学2019-2020学年高一上学期期末数学试题山西省朔州市怀仁县大地学校2019-2020学年高一上学期期末数学试题上海市实验学校2019-2020学年高一上学期期末数学试题海南省海口市琼山中学2020届上学期高三年级第一次月考数学试题上海市通河中学2021-2022学年高一上学期第二次阶段考试数学试题黑龙江省哈尔滨市尚志中学2021-2022学年高一上学期期中数学试题2004年普通高等学校招生考试数学(文)试题(上海卷)2004年普通高等学校招生考试数学(理)试题(上海卷)(已下线)高一数学上学期【第二次月考卷】(测试范围:第1章-第4章)-2022-2023学年高一数学考试满分全攻略(沪教版2020必修第一册)(已下线)第一章 集合与逻辑(易错必刷30题10种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)第4章 幂函数、指数函数与对数函数 单元测试卷-同步精品课堂(沪教版2020必修第一册)(已下线)4.4.2 对数函数的图象和性质(分层练习,五大题型)-同步精品课堂(人教A版2019必修第一册)上海市文来高中2023-2024学年高一上学期12月月考数学试题江苏省苏州市相城区望亭中学2023-2024学年高一上学期12月阶段性检测数学试卷(已下线)考点1 集合概念与基本关系 --2024届高考数学考点总动员【练】
10-11高一上·陕西西安·期中
名校
解题方法
2 . 某工厂生产某种零件的固定成本为20000元,每生产一个零件要增加投入100元,已知总收入 (单位:元)关于产量
(单位:元)关于产量 (单位:个)满足函数:
(单位:个)满足函数: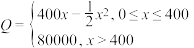 .
.
(1)将利润 (单位:元)表示为产量
(单位:元)表示为产量 的函数;(总收入=总成本+利润)
的函数;(总收入=总成本+利润)
(2)当产量为何值时,零件的单位利润最大?最大单位利润是多少元?(单位利润 利润
利润 产量)
产量)
 (单位:元)关于产量
(单位:元)关于产量 (单位:个)满足函数:
(单位:个)满足函数: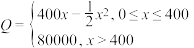 .
.(1)将利润
 (单位:元)表示为产量
(单位:元)表示为产量 的函数;(总收入=总成本+利润)
的函数;(总收入=总成本+利润)(2)当产量为何值时,零件的单位利润最大?最大单位利润是多少元?(单位利润
 利润
利润 产量)
产量)
您最近一年使用:0次
2023-09-19更新
|
751次组卷
|
103卷引用:2015-2016学年河南省鹤壁市淇一中高一下学期分班考试数学试卷
2015-2016学年河南省鹤壁市淇一中高一下学期分班考试数学试卷2015-2016学年四川省攀枝花市十五中高一上学期期中考试数学试卷2015-2016学年江西省鹰潭市一中高一11月月考数学试卷2015-2016学年福建省清流县一中高一上学期期中考试数学试卷2016-2017学年河北唐山曹妃甸一中高一上期中数学试卷【全国百强校】河南省安阳市第一中学2018-2019学年高一上学期第二阶段考试数学试题河南省平顶山市鲁山一中2019-2020学年高一上学期9月月考数学试题(已下线)2010年陕西省西安铁一中高一第一学期期中考试数学卷(已下线)2011-2012学年山东省兖州市高一上学期期中考试数学试卷(已下线)2011-2012学年浙江省宁波市慈湖中学高一上学期期中考试数学试卷(已下线)2011-2012学年广东省惠阳一中实验学校高一上学期期中数学试卷(已下线)2012-2013学年甘肃省天水市一中高一上学期期中数学试卷(已下线)2012-2013学年辽宁省五校协作体高一上学期期中考试数学试卷(已下线)2013-2014年学湖南省衡阳市八中高一上学期期末考试数学试卷(已下线)2014-2015学年河北唐山一中高一上学期期中考试数学试卷2014-2015学年广东省湛江市第一中学高一上学期期中考试数学试卷2014-2015学年河北省唐山一中高一上学期期中考试数学试卷2014-2015学年浙江省桐乡二中等三校高一上学期期中考试数学试卷2015-2016学年江苏省泰州中学高一创新班上期中数学试卷2015-2016学年广东省普宁市华美实验学校高一上学期期中数学试卷甘肃省会宁县第一中学2017-2018学年高一上学期第一次月考数学试题江西省樟树中学2017-2018学年高一上学期第一次月考数学试题广东省仲元中学2017-2018学年高一上学期期中考试数学试题2017-2018学年高中数学人教版A版必修一 第3章 3.2.2函数模型的应用实例4(已下线)活页作业25 实际问题的函数建模-2018年数学同步优化指导(北师大版必修1)广东省深圳市耀华实验学校2018-2019学年高一上学期期末考试数学试题沪教版 高一年级第一学期 领航者 第三章 单元测试宁夏回族自治区六盘山高级中学2019-2020学年高一上学期期中数学试题人教B版(2019) 必修第一册 过关斩将 第三章 3.3 函数的应用(一)&3.4 函数建模广东省佛山市第三中学2018-2019学年高一上学期期中数学试题江西省赣州市2019-2020学年高一上学期期中数学试题人教A版(2019) 必修第一册 过关斩将 第三章 3.4 函数的应用(一)人教A版(2019) 必修第一册 逆袭之路 第三章 函数的概念与性质 小结广东省梅州市2019-2020学年高一上学期期末数学试题(已下线)【新教材精创】3.3函数的应用(—)练习(2)-人教B版高中数学必修第—册湖北省黄冈市黄梅国际育才高级中学2019-2020学年高一上学期10月月考数学试题(已下线)第三章++函数的概念与性质章末综合检测-2020-2021学年高一数学课时同步练(新教材人教A版必修第一册)广西钦州市第一中学2020-2021学年高一10月月考数学试题湖南省岳阳市岳阳县第一中学、汨罗市第一中学2020-2021学年高一上学期第一次联考数学试题浙江省宁波市余姚中学2020-2021学年高一上学期10月质量检测数学试题吉林省乾安县第七中学2020-2021学年第一学期高一第二次质量检测数学(理)试题吉林省乾安县第七中学2020-2021学年第一学期高一第二次质量检测数学(文)试题(已下线)【新东方】双师 (63)山西省大同四中联盟学校2020-2021学年高一上学期期中数学试题(已下线)【新东方】【2021.5.25】【NB】【高一上】【高中数学】【NB00099】人教A版(2019) 必修第一册 新高考名师导学 第三章 复习参考题3云南省梁河县第一中学2020-2021学年高一上学期第二次月考数学试题新疆乌鲁木齐市第二十中学2020-2021学年高一上学期期中数学试题(已下线)3.4 函数的应用(一)(精讲)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第一册)(已下线)3.4 函数的应用(一)-2021-2022学年高一数学尖子生同步培优题典(人教A版2019必修第一册)(已下线)3.4 函数的应用(一)- 2021-2022高一上学期数学新教材配套提升训练(人教A版2019必修第一册)(已下线)第四章 指数函数与对数函数-2021-2022学年高一数学新教材单元过关测评卷(人教A版2019必修第一册)【学科网名师堂】甘肃省嘉峪关市第一中学2020-2021学年高二下学期期中考试数学(文)试题(已下线)考点10 函数模型及其应用-备战2022年高考数学(理)一轮复习考点帮(已下线)考点10 函数模型及其应用-备战2022年高考数学(文)一轮复习考点帮(已下线)专题3.9 函数的实际应用(练)- 2022年高考数学一轮复习讲练测(新教材新高考)宁夏固原市五原中学补习部2022届高三上学期期中考试数学(文)试题(已下线)复习参考题3新疆乌苏第一中学2021-2022学年高一上学期期中考试数学试题河北省邯郸市汇文中学2021-2022学年高一上学期11月月考数学试题(已下线)专题6.4 必修第一册(前三章)阶段测试题(难)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(人教A版2019必修第一册)(已下线)专题8.1 函数应用 章末检测1(易)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)第06讲 函数的应用(一)-【帮课堂】2021-2022学年高一数学同步精品讲义(人教A版2019必修第一册)(已下线)第08讲 函数模型的应用(二)-【帮课堂】2021-2022学年高一数学同步精品讲义(人教A版2019必修第一册)(已下线)专题3.4 函数的应用(一)-《聚能闯关》2021-2022学年高一数学提优闯关训练(人教A版2019必修第一册)(已下线)复习题三2(已下线)3.4 函数的应用(一)(基础知识+基本题型)--【一堂好课】2021-2022学年高一数学上学期同步精品课堂(人教A版2019必修第一册)(已下线)专题3.4 函数的应用(一)-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册) 新疆和硕县高级中学2021-2022学年高一上学期第二次月考数学试题(已下线)3.3 函数的应用(一)(已下线)专题21 函数的应用(一)(2)辽宁省沈阳市新民市第一高级中学2021-2022学年高一上学期期末考试数学试题广东省深圳市高级中学2021-2022学年高一上学期期中数学试题浙江省温州市永嘉县碧莲中学2021-2022学年高一上学期期中数学试题河北省邢台市六校2022-2023学年高一上学期期中数学试题天津市河西区2022-2023学年高一上学期期中数学试题福建省厦门双十中学2022-2023常年高一上学期期中考试数学试题浙江省嘉兴市八校联盟2022-2023学年高一上学期期中联考数学试题广东外语外贸大学实验中学2022-2023学年高一上学期阶段性训练数学试题福建省南平市浦城县2022-2023学年高一上学期期中考试数学试题山东省泰安市肥城市2022-2023学年高一上学期期中数学试题甘肃省酒泉市玉门市玉门油田第一中学2022-2023学年高一上学期期中数学试题黑龙江省鸡西市英桥高级中学2022-2023学年高二上学期期中考试数学试题2023年1月广东省普通高中学业水平合格性考试模拟三数学试题2022年黑龙江省普通高中学业水平合格性考试数学模拟试卷一福建福州外国语学校2022-2023学年高一上学期阶段性测试数学试题新疆生产建设兵团第二中学2022-2023学年高一上学期期末考试数学试题上海市上海中学2022届高三下学期高考模拟1数学试题广东省深圳外国语学校高中园2022-2023学年高一上学期学段(三)数学试题(已下线)8.2 函数与数学模型 (1)(已下线)第二章 综合测试B(提升卷)福建省福州外国语学校2022-2023学年高一上学期期中数学试题山东省单县第二中学2022-2023学年高二下学期阶段性考试数学试题(已下线)3.4 函数的应用(一)(精练)-《一隅三反》广东省汕尾市城区汕尾中学2022-2023学年高一下学期期中数学试题(已下线)第06讲 函数的应用(一)-【帮课堂】(人教A版2019必修第一册)新疆乌鲁木齐市第三十六中学2022-2023学年高一上学期期中考试数学试题新疆乌鲁木齐市第130中学2022-2023学年高一上学期期中考试数学试题山东省“学情空间”(聊城市第一实验学校等校)2024届高三上学期第一次阶段性测试数学试题广东省佛山市第一中学2023-2024学年高一上学期第一次教学质量检测(10月)数学试题(已下线)模块二 专题1 集合,简易逻辑与不等式 单元检测篇 A基础卷(已下线)模块一 专题2 函数的应用(人教A)2天津市静海区北师大静海实验学校2023-2024学年高一上学期第二次阶段检测(期中)数学试题
10-11高一上·广东中山·期中
名校
解题方法
3 . 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益 与投资额x成正比,且投资1万元时的收益为
与投资额x成正比,且投资1万元时的收益为 万元,投资股票等风险型产品的收益
万元,投资股票等风险型产品的收益 与投资额x的算术平方根成正比,且投资1万元时的收益为0.5万元.
与投资额x的算术平方根成正比,且投资1万元时的收益为0.5万元.
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
 与投资额x成正比,且投资1万元时的收益为
与投资额x成正比,且投资1万元时的收益为 万元,投资股票等风险型产品的收益
万元,投资股票等风险型产品的收益 与投资额x的算术平方根成正比,且投资1万元时的收益为0.5万元.
与投资额x的算术平方根成正比,且投资1万元时的收益为0.5万元.(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
您最近一年使用:0次
2023-09-19更新
|
211次组卷
|
101卷引用:2015-2016学年河南郑州宇华教育集团高一上抽考数学试卷
2015-2016学年河南郑州宇华教育集团高一上抽考数学试卷2015-2016学年福建省连江县尚德中学高一上学期期中考试数学试卷2015-2016学年四川省凉山州高一上学期期末数学试卷2015-2016学年山西省怀仁一中高一下期中理科数学试卷(已下线)同步君人教A版必修1第三章3.2.2 函数模型及其应用2016-2017学年福建福州外国语学校高一上期中数学试卷【全国百强校】河南省实验中学2018-2019学年高一上学期期中考试数学试题河南省郑州外国语学校2020-2021学年高一上学期第一次月考数学试题河南省郑州市第七高级中学2022-2023学年高一上学期学业质量测试数学试题(已下线)2011年广东省中山市实验高级中学高一上学期期中考试数学试卷(已下线)2012-2013学年重庆第49中学七校联盟高一上学期期中考试数学试卷(已下线)2014届陕西西安铁一中国际合作学校高三下第一次模拟考试文科数学试卷(已下线)2014届陕西省西安铁一中高三下学期第一次模拟文数学试卷2016届黑龙江省双鸭山一中高三上学期期中理科数学试卷2014-2015学年云南省玉溪市一中高一上学期期中数学试卷2016-2017年陕西西藏民族学院附中高一12月考数学试卷江苏省泰州中学2017-2018学年高一10月月考数学试题江苏省高邮一中2017-2018学年度高一上学期第一次学情调研数学试卷北京市第四中学2017-2018学年高一上学期期中考试数学试题高中数学人教版 必修1 第三章 函数的应用 3.2.2 函数模型的应用实例重庆市第八中学2017-2018学年高一上学期期末考试数学试题【全国百强校】广东省湛江第一中学2018-2019学年高一上学期第一次大考数学试题四川省眉山一中办学共同体2018-2019学年高一上学期半期考试数学试卷阶段质量评估4 函数应用-2018年数学同步优化指导(北师大版必修1)【全国百强校】福建省厦门市双十中学2018-2019学年高一上期中考试数学试题【校级联考】湖北省宜昌市协作体2018-2019学年高一上学期期末考试数学试题【市级联考】江西省赣州市2017-2018学年高一上学期期末考试数学试题【全国百强校】山东省日照市日照第一中学2018-2019学年高一上学期第二次阶段学习期中数学试题人教B版(2019) 必修第一册 必杀技 第三章 3.3函数的应用(一)人教A版(2019) 必修第一册 必杀技 第三章 3.4 函数的应用(一)江苏省南通市海安县南莫中学2019-2020学年高一上学期期中数学试题陕西省西安中学2019-2020学年高一上学期12月月考数学试题安徽省六安市舒城中学2019-2020学年高一上学期第一次月考数学试题四川省内江市威远中学2019-2020学年高一上学期期中数学试题福建省莆田市第六中学2019-2020学年高一上学期期中数学试题(B卷)重庆市外国语学校2018-2019学年高一上学期期末数学试题北京市陈经纶中学2019-2020学年高一上学期期中数学试题福建省莆田市第六中学2019-2020学年高一上学期期中数学试题(A卷)上海市松江二中2017-2018学年高一上学期12月月考数学试题海南省海南中学2019-2020学年高一上学期期末数学试题山东省潍坊市2018-2019学年高一上学期期中数学试题人教A版(2019) 必修第一册 逆袭之路 第三章 3.4 函数的应用(一)广东省中山市第一中学2018-2019学年高一上学期第二次段考数学试题专题12 函数的应用(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第一册)-《高中新教材知识讲学》江西省宜春市宜丰中学2019-2020学年高二下学期开学考试数学(文)试题安徽省六安市第一中学2019-2020学年高一上学期第二次段考数学试题贵州省织金县第二中学2019-2020学高一上学期期中考试数学试题内蒙古赤峰市2019-2020学年高一下学期期末联考(A卷)数学(文科)试题(已下线)综合测试(一)-2020-2021学年高一数学尖子生同步培优题典(人教A版2019必修第一册)山西省晋中市祁县中学校2019-2020学年高一上学期12月月考数学试题人教A版(2019) 必修第一册 过关斩将 第三章 3.2.1 单调性与最大(小)值 第二课时 函数的最大(小)值湖南省长沙市长郡中学2020-2021学年高一上学期期中数学试题重庆市第八中学2020-2021学年高一上学期第二次月考数学试题福建省厦门市第一中学2020-2021学年度高一数学12月适应性练习试题河北省正中实验中学2019-2020学年高一上学期第一次月考数学试题宁夏海原第一中学2020-2021学年高一上学期第二次月考数学试题(已下线)3.4 函数的应用-【新教材】人教A版(2019)高中数学必修第一册限时作业江苏省泰兴中学、南菁高级中学2020-2021学年高一(强化班)上学期第二次阶段考试数学试题(已下线)3.4 函数的应用(一)(精讲)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教版A版)(已下线)高一上学期期末全真模拟05-2020-2021学年高一数学期末考试高分直通车(沪教版2020,必修一)重庆市外国语学校2020-2021学年高一上学期12月月考数学试题(已下线)第08章 函数应用(A卷基础卷)-2020-2021学年高一数学必修第一册同步单元AB卷(新教材苏教版)全册综合测试模拟二 -【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第一册)-《高中新教材知识讲学》福建省泰宁第一中学2020-2021学年高一上学期学分认定暨第二次阶段考试数学试题江西省永丰县永丰中学2020-2021学年高一上学期期中考试数学试题(已下线)3.4 函数的应用(一)-2021-2022学年高一数学尖子生同步培优题典(人教A版2019必修第一册)(已下线)第三单元 (基础过关)函数的概念与性质 A卷-【双基双测】2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册)安徽省合肥市长丰县凤麟中学2020-2021学年高二下学期期中理科数学试题陕西省延安市黄陵中学2019-2020学年高一(普通班)上学期期末数学试题云南省昆明市第一中学2021-2022年高一上学期期中考数学试题广东省深圳技术大学附属中学2021-2022学年高一上学期期中数学试题四川省德阳市第五中学2021-2022学年高一年上学期第二次月考数学试题河北正中实验中学2021-2022学年高一上学期期中数学试题第8章 函数应用(A卷·夯实基础)-2021-2022学年高一数学同步单元AB卷(苏教版2019必修第一册)【学科网名师堂】(已下线)专题3.7 函数的应用(一)-重难点题型精讲-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)福建省泉州市五校联考2021-2022学年高一上学期期中考试数学试题广东实验中学2021-2022学年高一上学期期末数学试题内蒙古霍林郭勒市第一中学2021-2022学年高一上学期期中考试数学试题黑龙江省鸡西实验中学2020-2021学年高一上学期第一次月考数学试题安徽省六安市霍邱县第一中学2021-2022学年高一上学期第二次段考数学试题(已下线)3.4函数的应用(一)A卷2023版 湘教版(2019) 必修第一册 突围者 第4章 第五节 函数模型及其应用2023版 北师大版(2019) 必修第一册 突围者 第五章 第二节 实际问题中的函数模型山东省济南市章丘区第四中学2019-2020学年高一上学期12月月考数学试题广东省三校2022-2023学年高一上学期综合测试数学试题福建省莆田市第四中学2021-2022学年高一上学期第二次月考数学试题广东省中山市第一中学2022-2023学年高一上学期第二次段考数学试题山东省济南市济南第三中学2022-2023学年高一上学期12月月考数学试题福建省福州第十一中学2022-2023学年高一上学期适应性训练(期中)数学试题广东省深圳大学附属实验中学2022-2023学年高一上学期期末数学试题(已下线)第8章 函数应用(基础卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)专题3.4 函数的应用(一)(3类必考点)-2022-2023学年高一数学必考点分类集训系列(人教A版2019必修第一册)5.2 实际问题中的函数模型 同步练习 -2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)专题3.7 函数的应用(一)-重难点题型精讲-2022-2023学年高一数学举一反三系列(人教A版2019必修第一册)广东省深圳市聚龙科学中学2022-2023学年高一下学期第二次中段考数学试题河北省保定市部分高中2023-2024学年高一上学期9月月考数学试题(已下线)模块一 专题2 函数的应用(人教A)2上海市闵行第三中学2023-2024学年高一上学期12月月考数学试题(已下线)8.2 函数与数学模型(六大题型)-【帮课堂】(苏教版2019必修第一册)广西平果市铝城中学2023-2024学年高一上学期期末模拟数学试题(一)河北省保定市部分学校2023-2024学年高一上学期1月联考数学试题
12-13高三上·上海·期中
名校
4 . 某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为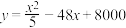 ,已知此生产线年产量最大为
,已知此生产线年产量最大为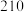 吨.
吨.
(1)求年产量为多少吨时,总成本最低,并求最低成本
(2)若每吨产品平均出厂价为 万元,那么当年产量为多少吨时,可以获得最大利润
万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
最大利润是多少
 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为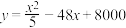 ,已知此生产线年产量最大为
,已知此生产线年产量最大为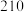 吨.
吨.(1)求年产量为多少吨时,总成本最低,并求最低成本

(2)若每吨产品平均出厂价为
 万元,那么当年产量为多少吨时,可以获得最大利润
万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
最大利润是多少
您最近一年使用:0次
2023-09-07更新
|
410次组卷
|
22卷引用:2015-2016学年河南省新乡延津高中高一下期中数学试卷
2015-2016学年河南省新乡延津高中高一下期中数学试卷2015-2016学年湖北省孝感六校联盟高一下学期期中考试文科数学卷2015-2016学年山东省临沂十八中高二下学期第一次月考文科数学试卷2015-2016学年江苏省泰兴一中高二下学期期中文科数学试卷2015-2016学年湖北省孝感市六校联盟高一下期中理科数学试卷2016-2017学年山西怀仁县一中高二上期开学考理数学试卷2016-2017学年山西怀仁县一中高二上期开学考文数学试卷2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(已下线)2012届上海市中国中学高三上学期期中考试文科数学试卷(已下线)2011-2012学年广东省执信中学高二上学期期末考试理科数学(已下线)2015届四川省成都市新都一中高三九月月考文科数学试卷2018届高三数学训练题(14 ):函数模型及其应用 (已下线)学科网2019年高考数学一轮复习讲练测2.9函数模型及其应用【江苏版】 练上海市七宝中学2015-2016学年高一上学期期中数学试题山西省晋中市平遥县综合职业技术学校2018-2019学年高三(普通班)上学期期中数学试题山东省临沂第十八中学2024届高三第一次调研考试数学试题河北省承德市第二中学2024届高三上学期开学初摸底数学试题(已下线)高一上学期期中复习【第三章 函数的概念与性质】十大题型归纳(基础篇)-举一反三系列(已下线)第四章 指数函数与对数函数 章末重难点归纳总结-《一隅三反》(已下线)3.4 函数的应用(一)(6大题型)精讲-【题型分类归纳】(人教A版2019必修第一册)宁夏回族自治区银川一中2023-2024学年高一上学期期中考试数学试题上海市上海中学东校2023-2024学年高一上学期期中考试数学试卷
名校
5 . 已知定义在 上的奇函数
上的奇函数 ,当
,当 时的解析式为
时的解析式为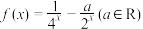 .
.
(1)求 在
在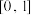 上的解析式;
上的解析式;
(2)求 在
在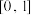 上的最大值.
上的最大值.
 上的奇函数
上的奇函数 ,当
,当 时的解析式为
时的解析式为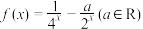 .
.(1)求
 在
在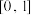 上的解析式;
上的解析式;(2)求
 在
在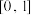 上的最大值.
上的最大值.
您最近一年使用:0次
2022-12-03更新
|
724次组卷
|
13卷引用:2015-2016学年河南省郑州一中高一下期入学考试数学试卷
2015-2016学年河南省郑州一中高一下期入学考试数学试卷2015-2016学年广东省普宁市华美实验学校高一上学期期中数学试卷甘肃省张掖市民乐县一中2018-2019学年高一上学期期中考试数学试题陕西省渭南市韩城市2018-2019学年高三下学期期中数学(理)试题辽宁省辽阳市东南协作校2019-2020学年高三上学期9月份月考数学理科试题内蒙古通辽市开鲁县第一中学2020-2021学年高一上学期期中考试数学(理)试题陕西省咸阳市泾阳县泾干中学2020-2021学年高一上学期第五次月考数学试题黑龙江省哈尔滨师范大学附属中学2022-2023学年高一上学期期中考试数学试题湖北省恩施市第一中学2022-2023学年高一上学期12月月考数学试题第三章 指数运算与指数函数 单元测试-2022-2023学年高一上学期数学北师大版(2019)必修第一册湖北省十堰市房县第一中学2022-2023学年高一上学期第二次阶段性考试数学试题广东省佛山市南海区石门中学2023-2024学年高一上学期期中考试数学试卷(已下线)第01讲 4.1指数+4.2指数函数—【练透核心考点】
名校
6 . 已知函数 ,在区间
,在区间 上有最大值4,最小值1,设
上有最大值4,最小值1,设 .
.
(1)求 的值;
的值;
(2)不等式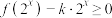 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)方程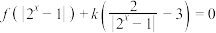 有三个不同的实数解,求实数k的取值范围
有三个不同的实数解,求实数k的取值范围
 ,在区间
,在区间 上有最大值4,最小值1,设
上有最大值4,最小值1,设 .
.(1)求
 的值;
的值;(2)不等式
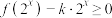 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(3)方程
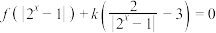 有三个不同的实数解,求实数k的取值范围
有三个不同的实数解,求实数k的取值范围
您最近一年使用:0次
2021-09-04更新
|
2040次组卷
|
44卷引用:2016-2017学年河南郑州一中高一上期中数学试卷
2016-2017学年河南郑州一中高一上期中数学试卷2015-2016学年江苏省淮阴中学高一上学期期中数学试卷22017届上海市实验学校高三9月月考数学试卷2015-2016学年江苏省淮阴中学高一上学期期中数学试卷12016-2017学年辽宁省庄河市高级中学高一上学期期末考试理数试卷2016-2017学年辽宁省庄河市高级中学高一上学期期末考试数学(理)试卷江苏省常州市横林高级中学2017~2018学年第一学期月考高三理科数学试卷安徽省六安市第一中学2018届高三上学期第二次月考数学(理)试题四川省双流中学2017-2018学年高一上学期期中考试数学试题安徽师范大学附属中学2017-2018学年高一上学期期中考试数学试题福建省闽侯第六中学2017-2018学年高二12月月考数学(文)试题广东省揭阳市第一中学2017-2018学年高一下学期第一次月考数学(理)试题(已下线)2019年一轮复习讲练测【新课标版文】专题2.8 函数与方程(测)(已下线)2019年一轮复习讲练测【新课标版理】专题2.3 函数的单调性与最值(测)(已下线)2019年一轮复习讲练测【新课标版文】专题2.3 函数的单调性与最值(测)【全国百强校】江苏省启东中学2018-2019学年高一上学期第二次月考数学试题1【市级联考】四川省雅安市2018-2019学年高一上学期期末考试数学试题上海市曹杨中学2018-2019学年高一上学期期末数学试题四川省成都市新津中学2019-2020学年高一上学期12月月考数学试题吉林省白城市通榆县第一中学2019-2020学年高二上学期第三次月考数学(文)试题黑龙江省哈尔滨市第六中学2019-2020学年高一上学期期末数学试题山西省太原市第五中学2019-2020学年高一上学期11月月考数学试题(已下线)专题04 一元二次不等式和分式不等式-2021届江苏省新高考数学大讲坛大一轮复习福建省福州格致中学2020-2021学年高一下学期期中考数学试题四川省新津中学2020-2021学年下学期高一入学考试数学试题高中数学解题兵法 第五讲 联用函数与方程思想黑龙江省哈尔滨市第六中学校2020-2021学年高一上学期质量检测数学试题福建省莆田第二中学2019-2020学年高一上学期期末数学试题(已下线)第4章指数函数与对数函数-【新教材】人教A版(2019)高中数学必修第一册同步练习(原卷+解析)湖北省宜昌市夷陵中学2021-2022学年高二上学期10月阶段性检测数学试题2016-2017学年黑龙江省大庆第一中学高一上学期期末考试数学试卷福建省泉州第五中学2021-2022学年高一上学期期中考试数学试题(已下线)专题二 指对幂函数及三角函数广东省中山市中山纪念中学2021-2022学年高一上学期第二次段考数学试题湖南省长沙市长郡中学2021-2022学年高一上学期期末数学试题安徽省六安市第一中学2021-2022学年高一下学期开学考试数学试题(已下线)第四章 指数函数与对数函数 综合检测-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)安徽省蚌埠第二中学2022-2023学年高二上学期8月月考数学试题山东省实验中学2022-2023学年高一上学期期中数学试题江西省名校2022-2023学年高一上学期第三次大联考数学试题(三)广东省广州五中2022-2023学年高一下学期开学考数学试题(已下线)高一上学期期末【常考60题考点专练】-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)(已下线)第13讲函数的应用(二)(5大考点)(2)湖南省长沙市周南中学2023-2024学年高二上学期第一次阶段考试数学试题
名校
解题方法
7 . 已知集合A={x|3≤x<6},B={x|2<x<9}.
(1)求A∩B,(∁RB)∪A;
(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值范围.
(1)求A∩B,(∁RB)∪A;
(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值范围.
您最近一年使用:0次
2021-08-22更新
|
954次组卷
|
47卷引用:2015-2016学年河南省鹤壁市淇一中高一下学期分班考试数学试卷
2015-2016学年河南省鹤壁市淇一中高一下学期分班考试数学试卷2015-2016学年山东省济宁市微山一中高一下入学检测数学试卷2016-2017学年河北武邑中学高一上周考9.11数学试卷河南省新乡市原阳县南街中学2021-2022学年高一上学期第一阶段考试数学试题2015-2016学年陕西省西安市第七十中学高一10月月考数学试卷2015-2016学年江西新余一中高一上第一次段考数学试卷(已下线)江西省上饶县中学2013-2014学年高一上学期第一次周考数学试题甘肃省甘谷县第一中学2017-2018学年高一上学期第一次月考数学试题湖南师范大学附属中学2017-2018学年高一上学期第一次阶段性检测数学试题湖北省襄阳市四校(襄州一中、枣阳一中、宜城一中、曾都一中)2017-2018学年高一上学期期中联考数学试题(已下线)第一章 章末复习课(课时作业)-2018版步步高学案导学与随堂笔记数学(北师大版必修1)甘肃省兰州十八中2017-2018学年高一上学期第一次月考数学试题湖南省地质中学2019-2020学年度高一上学期期中数学试题山西省运城市盐湖五中2019-2020学年高一上学期9月月考数学试题湖北省武汉为明学校2019-2020学年高一上学期第一次阶段考试数学试题新疆伊犁哈萨克自治州伊宁市第八中学2019-2020学年高一上学期期中考试数学试题衔接点15 集合的基本运算-2020年【衔接教材·暑假作业】初高中衔接数学(新人教版)衔接点15 集合的基本运算-2020年【衔接教材·暑假作业】初高中衔接数学(人教版)(已下线)[新教材精创]第一章集合练习-苏教版高中数学必修第一册(已下线)第1章集合与常用逻辑用语章末检测-【新教材】人教A版(2019)高中数学必修第一册限时作业(已下线)专题1.1集合单元测试(B卷提升篇)-2020-2021学年高一数学必修一同步单元AB卷(人教A版浙江专用)(已下线)第1章章末复习提升(同步学案,)-新教材2020-2021学年高一数学同步备课(人教B版必修第一册)河北省邢台市第七中学2018-2019学年高一上学期第一次月考(10月)数学试题河北省邢台市第七中学2019-2020学年高一(美术班)上学期第一次月考数学试题湖南省邵阳市邵东县创新实验学校2020-2021学年高三上学期第一次月考数学试题广东省东莞市第四高级中学2020-2021学年高一上学期10月月考数学试题福建省泉州实验中学2020-2021学年高一上学期第一阶段考试数学试题(已下线)专题1.1+集合(B卷提升篇)-2020-2021学年高一数学必修第一册同步单元AB卷(新教材人教B版)第一章+集合与常用逻辑用语(基础过关)-2020-2021学年高一数学单元测试定心卷(人教B版2019必修第一册)天津市静海区瀛海学校2020-2021学年高一上学期11月月考数学试题天津市静海区四校2020-2021学年高一上学期12月阶段性检测数学试题陕西省榆林市第十二中学2020-2021学年高一上学期第二次月考数学试题(已下线)练习1+集合-2020-2021学年【补习教材·寒假作业】高一数学(北师大2019版)陕西省西安市长安区第一中学2020-2021学年高一上学期第一次教学质量检测数学试题云南省大姚县第一中学2019-2020学年高一上学期期末数学试题(已下线)【师说智慧课堂】1.3.2集合的运算(二)检测题-2021-2022学年高中数学新教材同步练习江苏省苏州市吴中区2020-2021学年高一上学期期中数学试题陕西省安康中学2021-2022学年高一上学期第一次月考数学试题甘肃静宁县第一中学2021-2022学年高三上学期第二次模拟考试数学(文)试题陕西省西安市第一中学2021-2022学年高一上学期10月月考数学试题山东省潍坊高密市第三中学2022-2023学年高一上学期9月月考数学试题湖南省长沙市开物中学2022-2023学年高一上学期9月第一次月考数学试题B广东省广州市第一中学2022-2023学年高一上学期期中数学试题陕西省安康市汉滨区流水中学2021-2022学年高一上学期第一次月考数学试题广东省大坪镇大坪中学2020-2021学年高一上学期期末数学试题福建省南平市政和县第一中学2023-2024学年高一上学期第一次月考数学试题(已下线)第一章 集合(单元重点综合测试)-速记·巧练(苏教版2019必修第一册)
12-13高一上·河南·期中
名校
8 . 已知 ,
,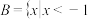 或
或 ,若
,若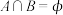 ,求
,求 的取值范围.
的取值范围.
 ,
,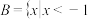 或
或 ,若
,若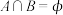 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-03-25更新
|
855次组卷
|
25卷引用:2015-2016学年河南省南阳市高一上学期期末数学试卷
2015-2016学年河南省南阳市高一上学期期末数学试卷(已下线)2012-2013学年河南省河南大学附属中学高一上期中考试数学试卷2015-2016学年湖南省岳阳一中高一上学期期中数学试卷河南省安阳市林州市林滤中学2019-2020学年高一上学期10月月考数学试题(已下线)2012年北师大版高中数学必修1 1.3集合的基本运算练习卷(已下线)2012-2013学年山西省忻州一中高一下学期期中考试数学文科试卷(已下线)2012-2013学年山西省忻州一中高一下学期期中考试数学理科试卷(已下线)2014-2015学年福建省漳州市平和县正兴学校高一9月月考数学试卷(已下线)江西省上饶县中学2013-2014学年高一上学期第一次周考数学试题安徽师范大学附属中学2017-2018学年高一上学期期中考试数学试题人教A版必修一第一章 集合与函数的概念 检测试卷12018年秋高中数学人教版必修一:单元评估验收(一)【全国百强校】青海省西宁市第四高级中学2018-2019学年高一上学期第一次月考数学试题人教B版(2019) 必修第一册 逆袭之路 第一章 集合与常用逻辑用语 整合提升人教A版(2019) 必修第一册(上) 重难点知识清单 第一章 集合与常用逻辑用语 1.3 集合的基本运算(已下线)1.3+第1课时+并集与交集(分层练习)-2020-2021学年高一数学新教材配套练习(人教A版必修第一册)(已下线)1.3集合的基本运算-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)(已下线)集合与常用逻辑用语(综合测试卷)-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)(已下线)1.3集合的基本运算-2020-2021学年高一数学同步课堂帮帮帮(人教A版2019必修第一册)陕西省咸阳市永寿县中学2020-2021学年高一上学期第一次月考数学试题河北省石家庄二十二中2020-2021学年高一上学期第一次月考数学试题(已下线)专题3 1.3 集合的基本运算 - 2021-2022高一上学期数学新教材配套提升训练(人教B版2019必修第一册)(已下线)《集合与常用逻辑用语》综合测试卷 - 2021-2022高一上学期数学新教材配套提升训练(人教A版2019必修第一册)(已下线)知识点 集合间的基本关系 易错点1 忽视空集1.1.3 集合的交与并 同步练习
名校
解题方法
9 . 若 是定义在
是定义在 上的增函数,且
上的增函数,且 .
.
(1)求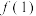 的值;
的值;
(2)若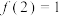 ,解不等式
,解不等式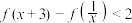 .
.
 是定义在
是定义在 上的增函数,且
上的增函数,且 .
.(1)求
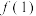 的值;
的值;(2)若
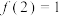 ,解不等式
,解不等式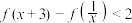 .
.
您最近一年使用:0次
2020-10-30更新
|
1634次组卷
|
17卷引用:2016-2017学年河南郑州一中高一上期中数学试卷
2016-2017学年河南郑州一中高一上期中数学试卷河南省郑州励德双语学校2023-2024学年高三上学期第一次月考数学试题2015-2016学年山东省济宁一中高一上学期期中考试数试卷辽宁省实验中学、沈阳市东北育才学校等五校2016-2017学年高二下学期期末联考文数试题(已下线)《2018-2019学年同步单元双基双测AB卷》必修一 专题三 函数的基本性质 B卷【全国百强校】贵州省铜仁市第一中学2018-2019学年高一上学期期中数学试题四川省成都市双流区棠湖中学2019-2020学年高一上学期第一次月考数学试题北京市首都师大附中2018~2019学年高一上学期10月月考数学试题山东省实验中学2019-2020学年高一上学期期中数学试题江西省奉新县第一中学2020-2021学年高一上学期第一次月考数学试题(已下线)练习11+抽象函数性质专题专题-2020-2021学年【补习教材·寒假作业】高一数学(北师大版)上海市上海师范大学附属第二外国语学校2017-2018学年高一上学期12月月考数学试题贵州省毕节市第一中学2021-2022学年高一上学期第二次阶段性考试数学试题云南省昆明市第十中学2021-2022学年高一10月第一次月考数学试题单调性与最大(小)值贵州省黔西南州金成实验学校2021-2022学年高一上学期期末数学试题云南省腾冲市2022-2023学年高一上学期期中教育教学质量监测数学试卷
名校
10 . 已知函数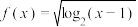 的定义域为集合
的定义域为集合 ,函数
,函数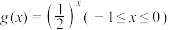 的值域为集合
的值域为集合 .
.
(1)求 ;
;
(2)若集合 ,且
,且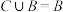 ,求实数
,求实数 的取值范围.
的取值范围.
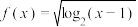 的定义域为集合
的定义域为集合 ,函数
,函数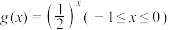 的值域为集合
的值域为集合 .
.(1)求
 ;
;(2)若集合
 ,且
,且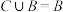 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2019-12-25更新
|
2027次组卷
|
13卷引用:2016-2017学年河南郑州一中高一上期中数学试卷
2016-2017学年河南郑州一中高一上期中数学试卷2017届江西省新余一中、宜春一中高三7月联考文科数学试卷【校级联考】安徽省安庆市五校联盟2018-2019学年高一上学期期中联考数学试卷【校级联考】福建省泉州市安溪一中、养正中学、惠安一中、泉州实验中学四校2018-2019学年高二(上)期中数学试题【校级联考】福建省闽侯二中五校教学联合体2018届高三上学期期中考试数学(文)试题黑龙江省绥化市安达七中2019-2020学年高一上学期期中数学试题辽宁省葫芦岛市普通高中2019-2020学年高一上学期期末数学试题福建省厦门市双十中学2019-2020学年高一上学期期中数学试题广东省江门市第二中学2019-2020学年高一上学期期中数学试题四川省成都市四川师范大学附属中学2020-2021学年高一上学期期中数学试题湖北省黄冈市外国语学校2020-2021学年高一上学期12月月考数学试题广东省深圳市宝安区2019-2020学年高一上学期期末数学数学试题江苏省扬州市仪征市第二中学2020-2021学年高三上学期12月第三次月考数学试题



