2024·全国·模拟预测
1 . 美国数学史家、穆伦堡学院名誉数学教授威廉・邓纳姆在1994年出版的The Mathematical Universe一书中写道:“相比之下,数学家达到的终极优雅是所谓的‘无言的证明’,在这样的证明中一个极好的令人信服的图示就传达了证明,甚至不需要任何解释.很难比它更优雅了.”如图所示正是数学家所达到的“终极优雅”,该图( 为矩形)完美地展示并证明了正弦和余弦的二倍角公式,则可推导出的正确选项为( )
为矩形)完美地展示并证明了正弦和余弦的二倍角公式,则可推导出的正确选项为( )
 为矩形)完美地展示并证明了正弦和余弦的二倍角公式,则可推导出的正确选项为( )
为矩形)完美地展示并证明了正弦和余弦的二倍角公式,则可推导出的正确选项为( )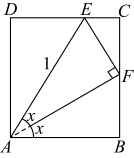
A. | B.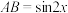 | C.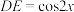 | D.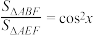 |
您最近半年使用:0次
名校
2 . 水车是古代中国劳动人民发明的灌溉工具,相传为汉灵帝时华岚造出雏形,经三国时孔明改造完善后在蜀国推广使用.作为中国农耕文化的重要组成部分,它体现了中华民族的创造力,为中国农业文明和水利史研究提供了见证.被誉为“水车之都”的兰州建起了一处水车博览园,再现了以前黄河两岸水车林立的壮观景象.如图为一架新制作的水车,其最高点距离水面为18米,最低点在水面下2米,该水车每 转一圈,若从水轮左侧距离水面3米的点处开始计算时间(假定水车逆时针方向旋转).
转一圈,若从水轮左侧距离水面3米的点处开始计算时间(假定水车逆时针方向旋转). 距离水面的高度
距离水面的高度 (单位:
(单位: )表示为时间
)表示为时间 (单位:
(单位: )的函数;
)的函数;
(2)在水轮转动的一圈内,有多长时间点 距水面的高度超过
距水面的高度超过 ?
?
 转一圈,若从水轮左侧距离水面3米的点处开始计算时间(假定水车逆时针方向旋转).
转一圈,若从水轮左侧距离水面3米的点处开始计算时间(假定水车逆时针方向旋转).
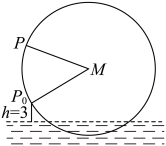
 距离水面的高度
距离水面的高度 (单位:
(单位: )表示为时间
)表示为时间 (单位:
(单位: )的函数;
)的函数;(2)在水轮转动的一圈内,有多长时间点
 距水面的高度超过
距水面的高度超过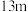 ?
?
您最近半年使用:0次
2024·全国·模拟预测
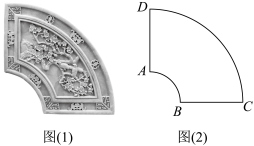
3 . 石雕、木雕、砖雕被称为建筑三雕.源远流长的砖雕,由东周瓦当、汉代画像砖等发展而来,明清时代进入巅峰,形成北京、天津、山西、徽州、广东、临夏以及苏派砖雕七大主要流派.苏派砖雕被称为“南方之秀”,是南方地区砖雕艺术的典型代表,被广泛运用到墙壁、门窗、檐廊、栏槛等建筑中.图(1)是一个梅花砖雕,其正面是一个扇环 ,如图(2),砖雕厚度为6cm,
,如图(2),砖雕厚度为6cm,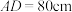 ,
, ,
, 所对的圆心角为直角,则该梅花砖雕的表面积为(单位:
所对的圆心角为直角,则该梅花砖雕的表面积为(单位: )( )
)( )
 ,如图(2),砖雕厚度为6cm,
,如图(2),砖雕厚度为6cm,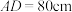 ,
, ,
, 所对的圆心角为直角,则该梅花砖雕的表面积为(单位:
所对的圆心角为直角,则该梅花砖雕的表面积为(单位: )( )
)( )
A.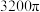 | B. | C. | D. |
您最近半年使用:0次
4 . 我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了晷影长 与太阳天顶距
与太阳天顶距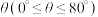 的对应数表,这是世界数学史上较早的正切函数表.根据三角学知识可知,晷影长
的对应数表,这是世界数学史上较早的正切函数表.根据三角学知识可知,晷影长 等于表高
等于表高 与太阳天顶距
与太阳天顶距 正切值的乘积,即
正切值的乘积,即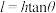 .对同一“表高”测量两次,第一次和第二次太阳天顶距分别为
.对同一“表高”测量两次,第一次和第二次太阳天顶距分别为 ,第二次的“晷影长”是“表高”的3倍,且
,第二次的“晷影长”是“表高”的3倍,且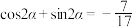 ,则
,则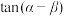 的值为( )
的值为( )
 与太阳天顶距
与太阳天顶距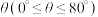 的对应数表,这是世界数学史上较早的正切函数表.根据三角学知识可知,晷影长
的对应数表,这是世界数学史上较早的正切函数表.根据三角学知识可知,晷影长 等于表高
等于表高 与太阳天顶距
与太阳天顶距 正切值的乘积,即
正切值的乘积,即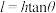 .对同一“表高”测量两次,第一次和第二次太阳天顶距分别为
.对同一“表高”测量两次,第一次和第二次太阳天顶距分别为 ,第二次的“晷影长”是“表高”的3倍,且
,第二次的“晷影长”是“表高”的3倍,且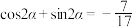 ,则
,则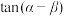 的值为( )
的值为( )A.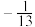 | B. | C.4 | D.13 |
您最近半年使用:0次
名校
解题方法
5 . 青花瓷 ,又称白地青花瓷,常简称青花,是中国瓷器的主流品种之一,属釉下彩瓷.原始青花瓷于唐宋已见端倪,成熟的青花瓷则出现在元代景德镇的湖田窑.图一是一个由波涛纹和葡萄纹构成的正六边形青花瓷盘,已知图二中正六边形的边长为2,圆
,又称白地青花瓷,常简称青花,是中国瓷器的主流品种之一,属釉下彩瓷.原始青花瓷于唐宋已见端倪,成熟的青花瓷则出现在元代景德镇的湖田窑.图一是一个由波涛纹和葡萄纹构成的正六边形青花瓷盘,已知图二中正六边形的边长为2,圆 的圆心为正六边形的中心,半径为1,若点
的圆心为正六边形的中心,半径为1,若点 在正六边形的边上运动,动点
在正六边形的边上运动,动点 在圆
在圆 上运动且关于圆心
上运动且关于圆心 对称,则
对称,则 的取值不可能是( )
的取值不可能是( )
 ,又称白地青花瓷,常简称青花,是中国瓷器的主流品种之一,属釉下彩瓷.原始青花瓷于唐宋已见端倪,成熟的青花瓷则出现在元代景德镇的湖田窑.图一是一个由波涛纹和葡萄纹构成的正六边形青花瓷盘,已知图二中正六边形的边长为2,圆
,又称白地青花瓷,常简称青花,是中国瓷器的主流品种之一,属釉下彩瓷.原始青花瓷于唐宋已见端倪,成熟的青花瓷则出现在元代景德镇的湖田窑.图一是一个由波涛纹和葡萄纹构成的正六边形青花瓷盘,已知图二中正六边形的边长为2,圆 的圆心为正六边形的中心,半径为1,若点
的圆心为正六边形的中心,半径为1,若点 在正六边形的边上运动,动点
在正六边形的边上运动,动点 在圆
在圆 上运动且关于圆心
上运动且关于圆心 对称,则
对称,则 的取值不可能是( )
的取值不可能是( )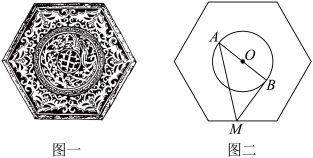
A. | B.2 | C. | D.3 |
您最近半年使用:0次
6 . 某导航通讯的信号可以用函数 近似模拟,若函数
近似模拟,若函数 在
在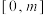 上有3个零点,则实数
上有3个零点,则实数 的取值范围为( )
的取值范围为( )
 近似模拟,若函数
近似模拟,若函数 在
在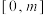 上有3个零点,则实数
上有3个零点,则实数 的取值范围为( )
的取值范围为( )A.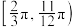 | B. | C. | D.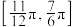 |
您最近半年使用:0次
2024-04-20更新
|
257次组卷
|
2卷引用:四川省百师联盟2024届高三冲刺卷(五)全国卷理科数学试题
解题方法
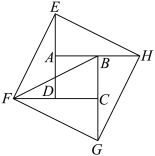
7 . 大约在公元222年,赵爽为《周髀算经》一书作注时介绍了“勾股圆方图”,即“赵爽弦图”.如图是某同学绘制的赵爽弦图,其中四边形 均为正方形,
均为正方形, ,则
,则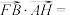
__________ .
 均为正方形,
均为正方形, ,则
,则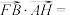
您最近半年使用:0次
2024-04-19更新
|
582次组卷
|
2卷引用:河南省濮阳市2024届高三下学期(开学)第一次模拟考试数学试题
名校
8 . 重庆荣昌折扇是中国四大名扇之一,荣昌折扇平面图为下图的扇形 ,其中
,其中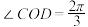 ,
,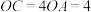 ,动点
,动点 在
在 上(含端点),连结
上(含端点),连结 交扇形
交扇形 的弧
的弧 于点Q,且
于点Q,且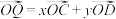 ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,其中
,其中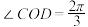 ,
,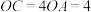 ,动点
,动点 在
在 上(含端点),连结
上(含端点),连结 交扇形
交扇形 的弧
的弧 于点Q,且
于点Q,且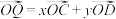 ,则下列说法正确的是( )
,则下列说法正确的是( )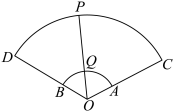
A.若 ,则 ,则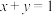 | B.若 ,则 ,则 |
C.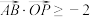 | D. |
您最近半年使用:0次
名校
解题方法
9 . 著名数学家华罗庚先生被誉为“中国现代数学之父”,他倡导的“0.618优选法”又称黄金分割法在生产和科研实践中得到了非常广泛的应用经研究,黄金分割比 还可以表示成
还可以表示成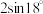 ,则
,则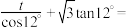 ( )
( )
 还可以表示成
还可以表示成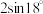 ,则
,则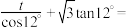 ( )
( )| A.4 | B.2 | C.1 | D. |
您最近半年使用:0次
名校
10 . 十七世纪法国数学家、被誉为业余数学家之王的皮埃尔·德·费马提出一个著名的几何问题:已知一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小.其答案如下:当三角形的三个角均小于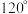 时,所求的点为三角形的正等角中心,即该点与三角形三个顶点的连线两两成
时,所求的点为三角形的正等角中心,即该点与三角形三个顶点的连线两两成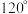 角;当三角形有一内角大于或等于
角;当三角形有一内角大于或等于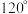 时,所求的点为三角形最大内角的顶点.在费马问题中所求的点被称为费马点.已知
时,所求的点为三角形最大内角的顶点.在费马问题中所求的点被称为费马点.已知 分别是
分别是 的内角
的内角 的对边,且
的对边,且 ,若
,若 为
为 的费马点,则
的费马点,则 ( )
( )
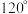 时,所求的点为三角形的正等角中心,即该点与三角形三个顶点的连线两两成
时,所求的点为三角形的正等角中心,即该点与三角形三个顶点的连线两两成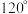 角;当三角形有一内角大于或等于
角;当三角形有一内角大于或等于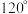 时,所求的点为三角形最大内角的顶点.在费马问题中所求的点被称为费马点.已知
时,所求的点为三角形最大内角的顶点.在费马问题中所求的点被称为费马点.已知 分别是
分别是 的内角
的内角 的对边,且
的对边,且 ,若
,若 为
为 的费马点,则
的费马点,则 ( )
( )| A.-1 | B.-2 | C.-3 | D.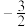 |
您最近半年使用:0次
2024-04-12更新
|
273次组卷
|
4卷引用:河北省沧州市沧县中学等校2023-2024学年高一下学期3月联考数学试题



