解题方法
1 . 已知椭圆 的离心率为
的离心率为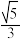 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,上、下顶点分别为
,上、下顶点分别为 ,
, ,且四边形
,且四边形 的面积为12.
的面积为12.
(1)求 的方程;
的方程;
(2)过点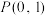 的直线
的直线 交
交 于M,N两点(不同于
于M,N两点(不同于 ,
, 两点),直线
两点),直线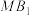 与直线
与直线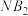 交于点
交于点 ,试判断
,试判断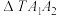 的面积是否为定值?若是,求出此定值;若不是,请说明理由.
的面积是否为定值?若是,求出此定值;若不是,请说明理由.
 的离心率为
的离心率为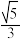 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,上、下顶点分别为
,上、下顶点分别为 ,
, ,且四边形
,且四边形 的面积为12.
的面积为12.(1)求
 的方程;
的方程;(2)过点
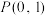 的直线
的直线 交
交 于M,N两点(不同于
于M,N两点(不同于 ,
, 两点),直线
两点),直线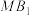 与直线
与直线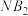 交于点
交于点 ,试判断
,试判断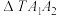 的面积是否为定值?若是,求出此定值;若不是,请说明理由.
的面积是否为定值?若是,求出此定值;若不是,请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 在同一平面直角坐标系中,P,Q分别是函数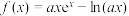 和
和 图象上的动点,若对任意
图象上的动点,若对任意 ,有
,有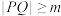 恒成立,则实数m的最大值为
恒成立,则实数m的最大值为______ .
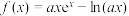 和
和 图象上的动点,若对任意
图象上的动点,若对任意 ,有
,有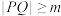 恒成立,则实数m的最大值为
恒成立,则实数m的最大值为
您最近一年使用:0次
2023-04-13更新
|
4985次组卷
|
8卷引用:安徽省滁州市定远中学2023届高三下学期5月调研考试数学试卷
安徽省滁州市定远中学2023届高三下学期5月调研考试数学试卷湖北省武汉市2023届高三下学期四月调研数学试题广东省2024届高三数学新改革适应性训练一(九省联考题型)广东省肇庆市肇庆中学2023届高三下学期4月月考数学试题湖南省长沙市第一中学2024届高三数学新改革适应性训练一(九省联考题型)(已下线)(新高考新结构)2024年高考数学模拟卷(二)(已下线)压轴第6题 利用导数求两动点的距离最值湖南省吉首市2024届高三下学期5月模拟考试数学试题
名校
3 . 已知抛物线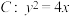 的焦点为
的焦点为 ,点
,点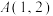 ,
, ,
, 为抛物线上不与
为抛物线上不与 重合的动点,
重合的动点, 为坐标原点,则下列说法中,正确的有( )
为坐标原点,则下列说法中,正确的有( )
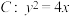 的焦点为
的焦点为 ,点
,点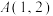 ,
, ,
, 为抛物线上不与
为抛物线上不与 重合的动点,
重合的动点, 为坐标原点,则下列说法中,正确的有( )
为坐标原点,则下列说法中,正确的有( )A.若 中点纵坐标为2,则 中点纵坐标为2,则 的斜率为2 的斜率为2 |
B.若点 恰为 恰为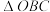 的垂心,则 的垂心,则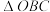 的周长为 的周长为 |
C.若 与 与 的倾斜角互补,则 的倾斜角互补,则 的斜率恒为 的斜率恒为 |
D.若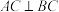 ,则 ,则 点纵坐标的取值范围是 点纵坐标的取值范围是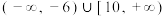 |
您最近一年使用:0次
2023-03-26更新
|
1120次组卷
|
2卷引用:安徽省定远中学2023届高三下学期第一次模拟检测数学试卷
名校
解题方法
4 . 已知函数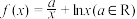 .
.
(1)讨论 的单调性;
的单调性;
(2)若 有两个不相同的零点
有两个不相同的零点 ,设
,设 的导函数为
的导函数为 .证明:
.证明: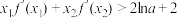 .
.
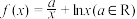 .
.(1)讨论
 的单调性;
的单调性;(2)若
 有两个不相同的零点
有两个不相同的零点 ,设
,设 的导函数为
的导函数为 .证明:
.证明: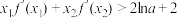 .
.
您最近一年使用:0次
2022-11-21更新
|
1387次组卷
|
11卷引用:安徽省滁州市定远县育才学校2023届高三下学期第一次模拟数学试题
安徽省滁州市定远县育才学校2023届高三下学期第一次模拟数学试题安徽省滁州市定远县民族中学2022-2023学年高三下学期开学考试数学试题贵州省六盘水市2021-2022学年高二下学期期末质量监测数学(理)试题(已下线)专题3-9 利用导函数研究极值点偏移问题(已下线)第五章 一元函数的导数及其应用(A卷·知识通关练)(5)(已下线)专题17 盘点利用导数证明不等式的五种方法-2(已下线)专题05导数及其应用(解答题)(已下线)专题22极值点偏移问题四川省江油市太白中学2022-2023学年高三下学期高考模拟(三)数学试题(已下线)第五章 一元导数及其应用章末重点题型归纳(3)福建师范大学附属中学2023届高三上学期12月月考数学试题
名校
5 . 已知函数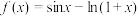 ,
, 为
为 的导数.
的导数.
(1)判断并证明 在区间
在区间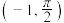 上存在的极大值点个数;
上存在的极大值点个数;
(2)判断 的零点个数.
的零点个数.
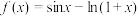 ,
, 为
为 的导数.
的导数.(1)判断并证明
 在区间
在区间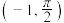 上存在的极大值点个数;
上存在的极大值点个数;(2)判断
 的零点个数.
的零点个数.
您最近一年使用:0次
2022-09-06更新
|
904次组卷
|
5卷引用:安徽省滁州市定远县第三中学2022-2023学年高三上学期9月月考数学试题
安徽省滁州市定远县第三中学2022-2023学年高三上学期9月月考数学试题四川省遂宁市射洪中学2022-2023学年高三上学期入学考试数学理试题(已下线)9.6 导数的综合运用(精练)(已下线)浙江省衢州、丽水、湖州三地市2022届高三(二模)数学试题变式题17-22(已下线)第九章 导数与三角函数的联袂 专题二 导数法求含三角函数的函数极值与最值 微点2 导数法求含三角函数的函数极值与最值(二)
名校
解题方法
6 . 已知函数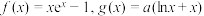 .
.
(1)若不等式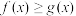 恒成立,求正实数a的值;
恒成立,求正实数a的值;
(2)证明: .
.
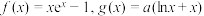 .
.(1)若不等式
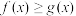 恒成立,求正实数a的值;
恒成立,求正实数a的值;(2)证明:
 .
.
您最近一年使用:0次
2022-04-21更新
|
1620次组卷
|
5卷引用:安徽省滁州市定远县育才学校2021-2022学年高三5月教学质量检测数学(理)试题
安徽省滁州市定远县育才学校2021-2022学年高三5月教学质量检测数学(理)试题湖北省2022届高三下学期4月调研(二模)数学试题(已下线)2022年高考考前20天终极冲刺攻略(一)【理科数学】(5月20日)(已下线)三轮冲刺卷06-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)福建省福州格致中学2023届高三上学期第二次月考(10月)数学试题
名校
解题方法
7 . 已知数列 和
和 ,
, 且
且 ,函数
,函数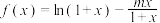 ,其中
,其中 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若数列 各项均为正整数,且对任意的
各项均为正整数,且对任意的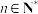 都有
都有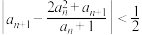 .求证:
.求证:
(ⅰ)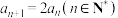 ;
;
(ⅱ) ,其中
,其中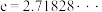 为自然对数的底数.
为自然对数的底数.
 和
和 ,
, 且
且 ,函数
,函数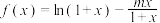 ,其中
,其中 .
.(1)求函数
 的单调区间;
的单调区间;(2)若数列
 各项均为正整数,且对任意的
各项均为正整数,且对任意的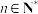 都有
都有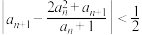 .求证:
.求证:(ⅰ)
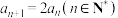 ;
;(ⅱ)
 ,其中
,其中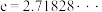 为自然对数的底数.
为自然对数的底数.
您最近一年使用:0次
2022-04-07更新
|
919次组卷
|
3卷引用:安徽省滁州市2022届高三下学期第二次教学质量检测理科数学试题
名校
8 . 已知函数 .
.
(1)当m=1时,求f(x)在[1,e]上的值域;
(2)设函数f(x)的导函数为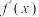 ,讨论
,讨论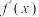 零点的个数.
零点的个数.
 .
.(1)当m=1时,求f(x)在[1,e]上的值域;
(2)设函数f(x)的导函数为
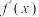 ,讨论
,讨论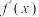 零点的个数.
零点的个数.
您最近一年使用:0次
2022-03-25更新
|
1222次组卷
|
6卷引用:安徽省滁州市定远县育才学校2021-2022学年高三下学期第二次月考数学(理)试题
解题方法
9 . 已知 .
.
(1)求 在
在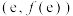 处的切线方程;
处的切线方程;
(2)若不等式 对任意
对任意 成立,求m的最大整数解.
成立,求m的最大整数解.
 .
.(1)求
 在
在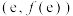 处的切线方程;
处的切线方程;(2)若不等式
 对任意
对任意 成立,求m的最大整数解.
成立,求m的最大整数解.
您最近一年使用:0次
2022-03-15更新
|
359次组卷
|
2卷引用:安徽省滁州市九校2021-2022学年高二下学期3月月考数学试题
名校
10 . 设函数 ,
, ,则下列说法正确的有( )
,则下列说法正确的有( )
 ,
, ,则下列说法正确的有( )
,则下列说法正确的有( )A.不等式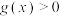 的解集为 的解集为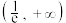 ; ; |
B.函数 在 在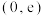 单调递增,在 单调递增,在 单调递减; 单调递减; |
C.当 时,总有 时,总有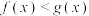 恒成立; 恒成立; |
D.若函数 有两个极值点,则实数 有两个极值点,则实数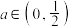 |
您最近一年使用:0次
2022-01-27更新
|
2234次组卷
|
15卷引用:安徽省定远中学2022-2023学年高二下学期6月第二次阶段性检测数学试卷
安徽省定远中学2022-2023学年高二下学期6月第二次阶段性检测数学试卷湖北省新高考联考协作体2021-2022学年高三上学期期末联考数学试题重庆市天星桥中学2022届高三上学期学业质量调研抽测(一)数学试题重庆市第八中学2022届高三下学期调研检测(二)数学试题重庆市璧山学校2021-2022学年高二下学期第一次月考数学试题重庆市万州第二高级中学2021-2022学年高二下学期期中数学试题重庆市万州纯阳中学校2021-2022学年高二下学期期中数学(A卷)试题湖北省武汉市第四十三中学2021-2022学年高二下学期期中数学试题山东省德州市第一中学2021-2022学年高二下学期6月月考数学试题江苏省常州市第一中学2022-2023学年高三上学期12月调研考试数学试题湖北省武汉市问津教育联合体2022-2023学年高二下学期3月质量检测数学试题甘肃省永昌县第一高级中学2022-2023学年高二下学期第一次月考数学试题安徽省阜南实验中学2022-2023学年高二下学期5月月考数学试题第二章 导数及其应用(B卷·提升能力)广西壮族自治区防城港市高级中学2022-2023学年高二下学期期中数学试题



