2024·全国·模拟预测
1 . 对于非空集合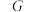 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在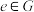 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得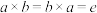 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意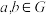 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群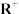 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群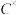 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
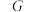 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
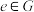 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得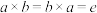 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意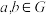 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
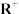 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群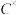 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近半年使用:0次
2 . 容器中有
 种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子,现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子,现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
①最后一颗粒子可能是A粒子;
②最后一颗粒子可能是B粒子;
③最后一颗粒子可能是C粒子;
其中正确结论的序号是______ .(写出所有正确结论的序号)

 种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子,现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:
种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子,现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:①最后一颗粒子可能是A粒子;
②最后一颗粒子可能是B粒子;
③最后一颗粒子可能是C粒子;
其中正确结论的序号是
您最近半年使用:0次
2023-02-08更新
|
756次组卷
|
4卷引用:广东省三校2022-2023学年高一下学期期中联考数学试题
3 . 设 为正整数,区间
为正整数,区间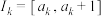 (其中
(其中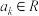 ,
,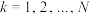 )同时满足下列两个条件:①对任意
)同时满足下列两个条件:①对任意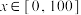 ,存在
,存在 使得
使得 ;②对任意
;②对任意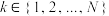 ,存在
,存在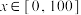 ,使得
,使得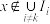 ,其中
,其中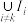 表示除
表示除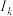 外的
外的 个集合的并集.
个集合的并集.
(1)若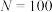 ,判断以下两个数列是否满足条件:①
,判断以下两个数列是否满足条件:①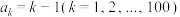 ;②
;②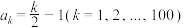 ?(结论不需要证明)
?(结论不需要证明)
(2)求 的最小值;
的最小值;
(3)判断 是否存在最大值,若存在,求
是否存在最大值,若存在,求 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
 为正整数,区间
为正整数,区间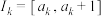 (其中
(其中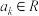 ,
,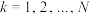 )同时满足下列两个条件:①对任意
)同时满足下列两个条件:①对任意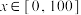 ,存在
,存在 使得
使得 ;②对任意
;②对任意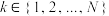 ,存在
,存在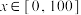 ,使得
,使得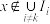 ,其中
,其中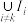 表示除
表示除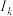 外的
外的 个集合的并集.
个集合的并集.(1)若
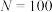 ,判断以下两个数列是否满足条件:①
,判断以下两个数列是否满足条件:①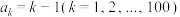 ;②
;②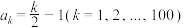 ?(结论不需要证明)
?(结论不需要证明)(2)求
 的最小值;
的最小值;(3)判断
 是否存在最大值,若存在,求
是否存在最大值,若存在,求 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
您最近半年使用:0次
2020-07-16更新
|
429次组卷
|
2卷引用:北京市朝阳区人大附中朝阳分校2022-2023学年高一上学期9月月考数学统练试题(1)
17-18高二下·上海宝山·阶段练习
4 . 设 是实系数一元二次方程
是实系数一元二次方程 的两个根,若
的两个根,若 是虚数,
是虚数,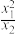 是实数,则
是实数,则 ( )
( )
 是实系数一元二次方程
是实系数一元二次方程 的两个根,若
的两个根,若 是虚数,
是虚数,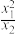 是实数,则
是实数,则 ( )
( )A. | B. | C. | D. |
您最近半年使用:0次
2019-12-07更新
|
3110次组卷
|
4卷引用:第九章 复数(压轴题专练)-单元速记·巧练(沪教版2020必修第二册)
(已下线)第九章 复数(压轴题专练)-单元速记·巧练(沪教版2020必修第二册)上海市宝山区宝山中学2017-2018学年高二下学期3月月考数学试题湖北省九校教研协作体2023届高三上学期起点考试数学试题湖北省部分名校2023届高考适应性考试数学试题
名校
5 . 已知集合 并且
并且 .定义
.定义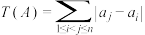 (例如:
(例如: ).
).
(1)若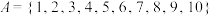 ,
,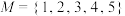 ,集合A的子集N满足:
,集合A的子集N满足: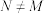 ,且
,且 ,求出一个符合条件的N;
,求出一个符合条件的N;
(2)已知集合 满足:
满足: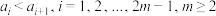 ,
,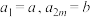 ,其中
,其中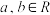 为给定的常数,求
为给定的常数,求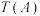 的取值范围.
的取值范围.
 并且
并且 .定义
.定义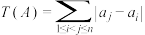 (例如:
(例如: ).
).(1)若
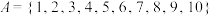 ,
,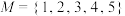 ,集合A的子集N满足:
,集合A的子集N满足: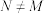 ,且
,且 ,求出一个符合条件的N;
,求出一个符合条件的N;(2)已知集合
 满足:
满足: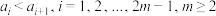 ,
,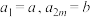 ,其中
,其中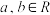 为给定的常数,求
为给定的常数,求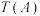 的取值范围.
的取值范围.
您最近半年使用:0次
6 . 已知数列 (其中第一项是
(其中第一项是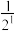 ,接下来的
,接下来的 项是
项是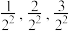 ,再接下来的
,再接下来的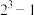 项是
项是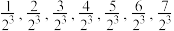 ,依此类推)的前
,依此类推)的前 项和为
项和为 ,下列判断:
,下列判断:
① 是
是 的第
的第 项;②存在常数
项;②存在常数 ,使得
,使得 恒成立;③
恒成立;③ ;④满足不等式
;④满足不等式 的正整数
的正整数 的最小值是
的最小值是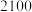 .
.
其中正确的序号是
 (其中第一项是
(其中第一项是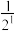 ,接下来的
,接下来的 项是
项是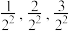 ,再接下来的
,再接下来的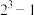 项是
项是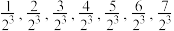 ,依此类推)的前
,依此类推)的前 项和为
项和为 ,下列判断:
,下列判断:①
 是
是 的第
的第 项;②存在常数
项;②存在常数 ,使得
,使得 恒成立;③
恒成立;③ ;④满足不等式
;④满足不等式 的正整数
的正整数 的最小值是
的最小值是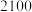 .
.其中正确的序号是
| A.①③ | B.①④ | C.①③④ | D.②③④ |
您最近半年使用:0次
2019-07-13更新
|
1262次组卷
|
3卷引用:广西南宁市第三中学、北海中学2020-2021学年高一6月联考数学试题
名校
7 . 十七世纪法国数学家费马提出猜想:“当整数 时,关于
时,关于 的方程
的方程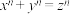 没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁
没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁 怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是
怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是
 时,关于
时,关于 的方程
的方程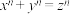 没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁
没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁 怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是
怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是A.存在至少一组正整数组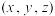 使方程 使方程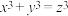 有解 有解 |
B.关于 的方程 的方程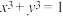 有正有理数解 有正有理数解 |
C.关于 的方程 的方程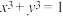 没有正有理数解 没有正有理数解 |
D.当整数 时,关于 时,关于 的方程 的方程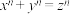 没有正实数解 没有正实数解 |
您最近半年使用:0次
2018-12-24更新
|
1115次组卷
|
9卷引用:上海市金山中学2020-2021学年高一上学期12月月考数学试题
上海市金山中学2020-2021学年高一上学期12月月考数学试题(已下线)专题04+常用逻辑用语(2)(反证法)-2020-2021学年新教材高一数学秋季辅导讲义(沪教版2020)上海市徐汇区位育中学2021-2022学年高一上学期期中数学试题(已下线)上海高一上学期期中【压轴42题专练】(1)(已下线)第1章 集合与逻辑(基础、典型、新文化、压轴)分类专项训练-2022-2023学年高一数学考试满分全攻略(沪教版2020必修第一册)【市级联考】四川省凉山州2019 届高中毕业班第一次诊断性检测数学(文)试题【市级联考】四川省凉山州2019 届高三第一次诊断性检测数学(理)试题(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021年高考数学(理)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法 (精练)-2021年高考数学(理)一轮复习学与练
8 . 设 是定义在R上的函数,对任意
是定义在R上的函数,对任意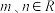 恒有
恒有 .当
.当 时,
时,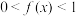 ,且
,且 .
.
(1)求证: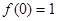 ;
;
(2)证明: 时恒有
时恒有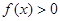 ;
;
(3)求证: 在
在 上是减函数;
上是减函数;
(4)若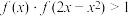 ,求
,求 的取值范围.
的取值范围.
 是定义在R上的函数,对任意
是定义在R上的函数,对任意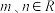 恒有
恒有 .当
.当 时,
时,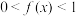 ,且
,且 .
.(1)求证:
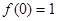 ;
; (2)证明:
 时恒有
时恒有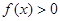 ;
;(3)求证:
 在
在 上是减函数;
上是减函数; (4)若
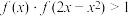 ,求
,求 的取值范围.
的取值范围.
您最近半年使用:0次



