1 . 对于函数 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为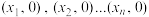 ,记
,记 为数列
为数列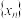 的第n项,则称数列
的第n项,则称数列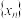 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为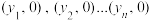 ,记
,记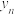 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”
(1)设函数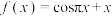 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.
(2)设函数 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.
(3)设复数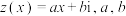 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为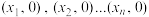 ,记
,记 为数列
为数列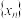 的第n项,则称数列
的第n项,则称数列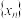 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为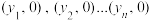 ,记
,记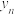 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”(1)设函数
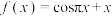 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.(2)设函数
 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.(3)设复数
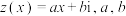 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
您最近一年使用:0次
2024-01-01更新
|
495次组卷
|
7卷引用:模块一专题1【练】《导数的概念、运算及其几何意义》单元检测篇B提升卷(人教A2019版)
(已下线)模块一专题1【练】《导数的概念、运算及其几何意义》单元检测篇B提升卷(人教A2019版)(已下线)模块二 专题1 与曲线的切线相关问题(已下线)模块二 专题3 与曲线的切线相关问题(人教B版)(已下线)模块二 专题4 与曲线的切线相关问题(高二北师大版)上海市普陀区桃浦中学2022-2023学年高二下学期期中数学试题(已下线)模块一 专题1 《导数的概念、运算及其几何意义》B提升卷(苏教版)(已下线)模块二 专题1 与曲线的切线相关问题(苏教版高二)
2 . 在复数域中,对于正整数 满足
满足 的所有复数
的所有复数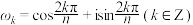 称为单位根,其中满足对任意小于
称为单位根,其中满足对任意小于 的正整数
的正整数 ,都有
,都有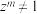 ,则称这种复数为
,则称这种复数为 次的本原单位根,例如当
次的本原单位根,例如当 时,存在四个4次单位根
时,存在四个4次单位根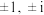 ,因为
,因为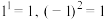 ,因此只有两个4次本原单位根
,因此只有两个4次本原单位根 .
.
(1)直接写出复数 的3次单位根,并指出那些是复数
的3次单位根,并指出那些是复数 的3次本原单位根(无需证明).
的3次本原单位根(无需证明).
(2)①若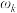 是复数
是复数 的8次本原单位根,证明:
的8次本原单位根,证明: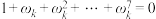 .
.
②若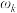 是复数
是复数 的
的 次本原单位根,证明:
次本原单位根,证明: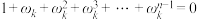 .
.
 满足
满足 的所有复数
的所有复数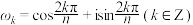 称为单位根,其中满足对任意小于
称为单位根,其中满足对任意小于 的正整数
的正整数 ,都有
,都有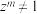 ,则称这种复数为
,则称这种复数为 次的本原单位根,例如当
次的本原单位根,例如当 时,存在四个4次单位根
时,存在四个4次单位根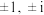 ,因为
,因为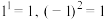 ,因此只有两个4次本原单位根
,因此只有两个4次本原单位根 .
.(1)直接写出复数
 的3次单位根,并指出那些是复数
的3次单位根,并指出那些是复数 的3次本原单位根(无需证明).
的3次本原单位根(无需证明).(2)①若
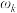 是复数
是复数 的8次本原单位根,证明:
的8次本原单位根,证明: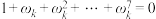 .
.②若
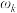 是复数
是复数 的
的 次本原单位根,证明:
次本原单位根,证明: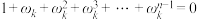 .
.
您最近一年使用:0次
名校
解题方法
3 . 在复平面内复数 ,
,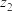 所对应的点为
所对应的点为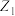 ,
,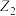 ,
, 为坐标原点,
为坐标原点, 是虚数单位.
是虚数单位.
(1) ,
,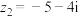 ,计算
,计算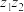 与
与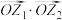 ;
;
(2)设 ,
,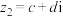
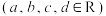 ,求证:
,求证: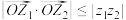 ,并指出向量
,并指出向量 ,
,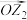 满足什么条件时该不等式取等号.
满足什么条件时该不等式取等号.
 ,
,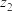 所对应的点为
所对应的点为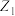 ,
,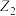 ,
, 为坐标原点,
为坐标原点, 是虚数单位.
是虚数单位.(1)
 ,
,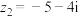 ,计算
,计算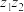 与
与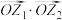 ;
;(2)设
 ,
,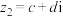
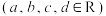 ,求证:
,求证: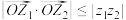 ,并指出向量
,并指出向量 ,
,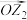 满足什么条件时该不等式取等号.
满足什么条件时该不等式取等号.
您最近一年使用:0次
2024-05-07更新
|
169次组卷
|
23卷引用:第5章复数章末十五种常考题型归类(2)-【帮课堂】(北师大版2019必修第二册)
(已下线)第5章复数章末十五种常考题型归类(2)-【帮课堂】(北师大版2019必修第二册)上海市嘉定区、长宁、金山区2019-2020学年高三上学期期末数学试题2020届上海市长宁嘉定金山高三一模数学试题2020届上海市嘉定区高三一模数学试题(已下线)热点04 平面向量、复数-2021年高考数学【热点·重点·难点】专练(上海专用)沪教版(2020) 必修第二册 高效课堂 册末测试卷沪教版(2020) 必修第二册 领航者 第9章 复数 9.2复数的几何意义 第1课时 复平面与复数的坐标、向量表示及复数加法的平行四边形法则沪教版(2020) 必修第二册 同步跟踪练习 第9章 复数 单元测试卷河北省石家庄市藁城新冀明中学2020-2021学年高一下学期(5月)第二次月考数学试题沪教版(2020) 必修第二册 领航者 一课一练 第9章 9.2 第1课时 复平面与复数的坐标、向量表示及复数加法的平行四边形法则(已下线)专题14 复数(模拟练)沪教版(2020) 必修第二册 单元训练 第9章 单元测试(B卷)沪教版(2020) 必修第二册 同步跟踪练习 第9章 测试卷(已下线)7.1.2 复数的几何意义(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)模块三 专题5 大题分类练(复数)基础夯实练(人教A)(已下线)模块三 专题6(复数)基础夯实练(北师大版)(已下线)第十二章 复数(单元重点综合测试)-单元速记·巧练(苏教版2019必修第二册)(已下线)12.3 复数的几何意义-【帮课堂】(苏教版2019必修第二册)重庆市缙云教育联盟2023-2024学年高一下学期3月月度质量检测数学试题(已下线)第七章 复数(提升卷)--重难点突破及混淆易错规避(人教A版2019必修第二册)山东省枣庄市第三中学2023-2024学年高一下学期期中考试数学试题(已下线)12.3-4 复数的几何意义、三角表示-2021-2022学年高一数学10分钟课前预习练(苏教版2019必修第二册)(已下线)模块三 专题7 大题分类练(复数)基础夯实练(苏教版)
名校
解题方法
4 . 现定义“ 维形态复数
维形态复数 ”:
”: ,其中
,其中 为虚数单位,
为虚数单位, ,
, .
.
(1)当 时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
(2)若“2维形态复数”与“3维形态复数”相等,求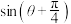 的值;
的值;
(3)若正整数 ,
,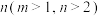 ,满足
,满足 ,
, ,证明:存在有理数
,证明:存在有理数 ,使得
,使得 .
.
 维形态复数
维形态复数 ”:
”: ,其中
,其中 为虚数单位,
为虚数单位, ,
, .
.(1)当
 时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;(2)若“2维形态复数”与“3维形态复数”相等,求
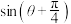 的值;
的值;(3)若正整数
 ,
,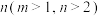 ,满足
,满足 ,
, ,证明:存在有理数
,证明:存在有理数 ,使得
,使得 .
.
您最近一年使用:0次
2024-05-11更新
|
1146次组卷
|
7卷引用:安徽省合肥市第一中学2023-2024学年高一下学期5月期中联考数学试题
安徽省合肥市第一中学2023-2024学年高一下学期5月期中联考数学试题广西南宁市第二中学2023-2024学年高一下学期5月月考数学试卷湖北省黄冈市浠水县第一中学2023-2024学年高一下学期期末质量检测数学试题(已下线)高一下学期期末模拟卷02-题型分类归纳讲与练(人教A版2019必修第二册)(已下线)拔高点突破02 平面向量与复数背景下的新定义问题(六大题型)湖南省三湘名校教育联盟联考2023-2024学年高一下学期期中考试数学试题海南省定安县定安中学2024-2025学年高二上学期开学考试数学试题
名校
解题方法
5 . 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受.形如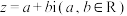 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当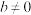 且时,
且时, 为纯虚数.其中
为纯虚数.其中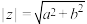 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,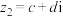 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成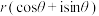 的形式,即
的形式,即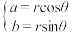 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定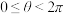 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.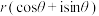 叫做复数
叫做复数 的三角形式.
的三角形式.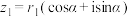 ,
,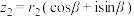 ,求
,求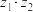 、
、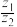 的三角形式;
的三角形式;
(2)设复数 ,
,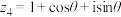 ,其中
,其中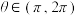 ,求
,求 ;
;
(3)在 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
① ;
;
②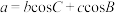 ,
,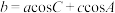 ,
,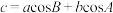 .
.
注意:使用复数以外的方法证明不给分.
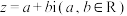 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当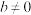 且时,
且时, 为纯虚数.其中
为纯虚数.其中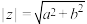 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,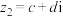 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成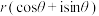 的形式,即
的形式,即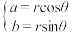 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定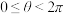 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.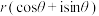 叫做复数
叫做复数 的三角形式.
的三角形式.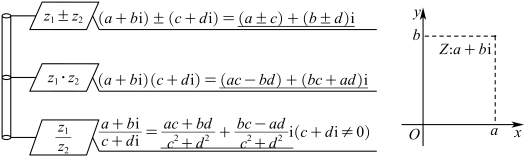
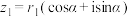 ,
,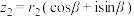 ,求
,求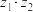 、
、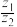 的三角形式;
的三角形式;(2)设复数
 ,
,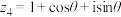 ,其中
,其中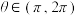 ,求
,求 ;
;(3)在
 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:①
 ;
;②
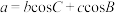 ,
,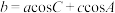 ,
,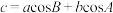 .
.注意:使用复数以外的方法证明不给分.
您最近一年使用:0次
2024-03-12更新
|
735次组卷
|
5卷引用:黑龙江省哈尔滨师范大学附属中学2023-2024学年高一下学期开学考试数学试卷
黑龙江省哈尔滨师范大学附属中学2023-2024学年高一下学期开学考试数学试卷(已下线)模块五 专题六 全真拔高模拟2(已下线)第七章:复数(新题型)-同步精品课堂(人教A版2019必修第二册)湖北省黄冈市浠水县第一中学2023-2024学年高一下学期期中考试数学试卷重庆市缙云教育联盟2023-2024学年高一下学期3月月度质量检测数学试题
6 . 对于非空集合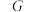 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在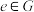 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得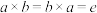 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意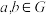 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群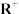 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群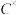 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
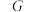 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
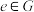 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得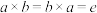 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意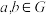 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
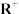 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群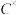 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近一年使用:0次
名校
解题方法
7 . 已知复数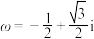 ,
,
(1)求证: ;
;
(2)化简: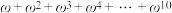 ;
;
(3)若 是方程
是方程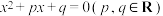 的一个根,求
的一个根,求 的值.
的值.
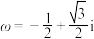 ,
,(1)求证:
 ;
;(2)化简:
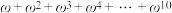 ;
;(3)若
 是方程
是方程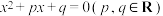 的一个根,求
的一个根,求 的值.
的值.
您最近一年使用:0次
名校
8 . 我们可以把平面向量坐标的概念推广为“复向量”,即可将有序复数对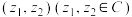 视为一个向量,记作
视为一个向量,记作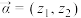 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量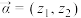 ,
, 的数量积记作
的数量积记作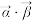 ,定义为
,定义为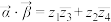 ;复向量
;复向量 的模定义为
的模定义为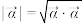 .
.
(1)设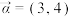 ,
,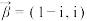 ,求复向量
,求复向量 与
与 的模;
的模;
(2)已知对任意的实向量 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;
①求证:对任意实数a,b,c,d,不等式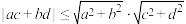 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;
②求证:对任意两个复向量 与
与 ,不等式
,不等式 仍然成立;
仍然成立;
(3)当 时,称复向量
时,称复向量 与
与 平行.设
平行.设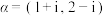 ,
,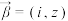 ,
,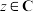 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
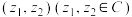 视为一个向量,记作
视为一个向量,记作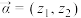 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量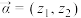 ,
, 的数量积记作
的数量积记作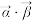 ,定义为
,定义为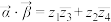 ;复向量
;复向量 的模定义为
的模定义为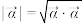 .
.(1)设
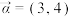 ,
,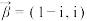 ,求复向量
,求复向量 与
与 的模;
的模;(2)已知对任意的实向量
 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;①求证:对任意实数a,b,c,d,不等式
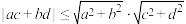 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;②求证:对任意两个复向量
 与
与 ,不等式
,不等式 仍然成立;
仍然成立;(3)当
 时,称复向量
时,称复向量 与
与 平行.设
平行.设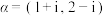 ,
,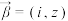 ,
,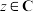 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
您最近一年使用:0次
2024-05-23更新
|
508次组卷
|
4卷引用:黑龙江省哈尔滨市第九中学校2023-2024学年高一下学期期中学业阶段评价考试数学试卷
黑龙江省哈尔滨市第九中学校2023-2024学年高一下学期期中学业阶段评价考试数学试卷(已下线)专题6 以新定义为背景的相关问题【练】(高一期末压轴专项)重庆市万州第二高级中学2024-2025学年高二上学期入学考试数学检测试卷山东省济宁市北大新世纪邹城实验学校2023-2024学年高一下学期期末考试数学试题
2024高一下·全国·专题练习
9 . 求证:
(1)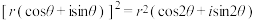 ;
;
(2) .
.
(1)
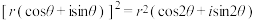 ;
;(2)
 .
.
您最近一年使用:0次

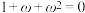 ;
;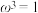 .
.


