名校
解题方法
1 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记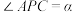 ,
,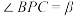 ,
, ,二面角
,二面角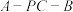 的大小为
的大小为 ,则
,则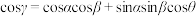 .如图2,四棱柱
.如图2,四棱柱 中,
中,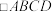 为菱形,
为菱形, ,
,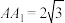 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.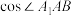 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: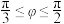 ;
;
(3)在直线 上是否存在点
上是否存在点 ,使
,使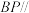 平面
平面 ?若存在,求出点
?若存在,求出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记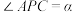 ,
,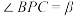 ,
, ,二面角
,二面角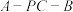 的大小为
的大小为 ,则
,则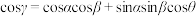 .如图2,四棱柱
.如图2,四棱柱 中,
中,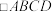 为菱形,
为菱形, ,
,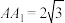 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
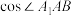 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: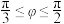 ;
;(3)在直线
 上是否存在点
上是否存在点 ,使
,使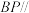 平面
平面 ?若存在,求出点
?若存在,求出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
2 . 在平面内,若直线 将多边形分为两部分,多边形在
将多边形分为两部分,多边形在 两侧的顶点到直线
两侧的顶点到直线 的距离之和相等,则称
的距离之和相等,则称 为多边形的一条“等线”.双曲线
为多边形的一条“等线”.双曲线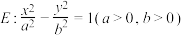 的左、右焦点分别为
的左、右焦点分别为 、
、 ,其离心率为
,其离心率为 ,且点
,且点 为双曲线
为双曲线 右支上一动点,直线
右支上一动点,直线 与曲线
与曲线 相切于点
相切于点 ,且与
,且与 的渐近线交于
的渐近线交于 、
、 两点,且点
两点,且点 在点
在点 上方.当
上方.当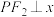 轴时,直线
轴时,直线 为
为 的等线.已知双曲线
的等线.已知双曲线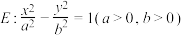 在其上一点
在其上一点 处的切线方程为
处的切线方程为 .
.
(1)求双曲线 的方程;
的方程;
(2)若 是四边形
是四边形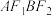 的等线,求四边形
的等线,求四边形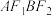 的面积;
的面积;
(3)已知 为坐标原点,设
为坐标原点,设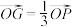 ,点
,点 的轨迹为曲线
的轨迹为曲线 ,证明:
,证明: 在点
在点 处的切线
处的切线 为
为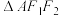 的等线.
的等线.
 将多边形分为两部分,多边形在
将多边形分为两部分,多边形在 两侧的顶点到直线
两侧的顶点到直线 的距离之和相等,则称
的距离之和相等,则称 为多边形的一条“等线”.双曲线
为多边形的一条“等线”.双曲线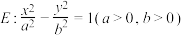 的左、右焦点分别为
的左、右焦点分别为 、
、 ,其离心率为
,其离心率为 ,且点
,且点 为双曲线
为双曲线 右支上一动点,直线
右支上一动点,直线 与曲线
与曲线 相切于点
相切于点 ,且与
,且与 的渐近线交于
的渐近线交于 、
、 两点,且点
两点,且点 在点
在点 上方.当
上方.当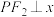 轴时,直线
轴时,直线 为
为 的等线.已知双曲线
的等线.已知双曲线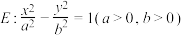 在其上一点
在其上一点 处的切线方程为
处的切线方程为 .
.(1)求双曲线
 的方程;
的方程;(2)若
 是四边形
是四边形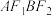 的等线,求四边形
的等线,求四边形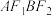 的面积;
的面积;(3)已知
 为坐标原点,设
为坐标原点,设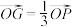 ,点
,点 的轨迹为曲线
的轨迹为曲线 ,证明:
,证明: 在点
在点 处的切线
处的切线 为
为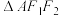 的等线.
的等线.
您最近一年使用:0次
2024-10-25更新
|
214次组卷
|
4卷引用:周测18 圆锥曲线(一轮好卷北京专版 )
(已下线)周测18 圆锥曲线(一轮好卷北京专版 )海南省某校2025届高三上学期第2次月考数学试题陕西省四校2025届高三上学期第二次质量检测联考数学试题江西省上饶市广信中学2025届高三上学期十月数学检测卷
名校
解题方法
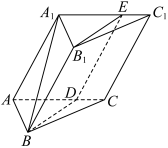
3 . 如图,三棱柱 中,四边形
中,四边形 是边长为4的菱形,
是边长为4的菱形,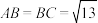 ,点
,点 为棱AC上动点(不与A,C重合),平面
为棱AC上动点(不与A,C重合),平面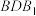 与棱
与棱 交于点
交于点 .
.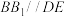 ;
;
(2)若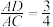 ,从条件①、条件②、条件③中选择两个条件作为已知,求直线
,从条件①、条件②、条件③中选择两个条件作为已知,求直线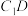 与平面
与平面 所成角的正弦值.
所成角的正弦值.
条件①: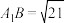
条件②:二面角 为直二面角
为直二面角
条件③: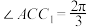 .
.
 中,四边形
中,四边形 是边长为4的菱形,
是边长为4的菱形,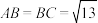 ,点
,点 为棱AC上动点(不与A,C重合),平面
为棱AC上动点(不与A,C重合),平面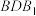 与棱
与棱 交于点
交于点 .
.
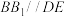 ;
;(2)若
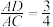 ,从条件①、条件②、条件③中选择两个条件作为已知,求直线
,从条件①、条件②、条件③中选择两个条件作为已知,求直线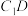 与平面
与平面 所成角的正弦值.
所成角的正弦值.条件①:
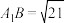
条件②:二面角
 为直二面角
为直二面角条件③:
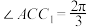 .
.
您最近一年使用:0次
名校
4 . 已知椭圆C:  的左、右焦点分别为
的左、右焦点分别为 、
、 ,一个焦点为
,一个焦点为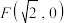 ,P是椭圆上一动点(与左、右顶点不重合).已知
,P是椭圆上一动点(与左、右顶点不重合).已知 的面积的最大值为2.
的面积的最大值为2.
(1)求椭圆C的方程;
(2)过点 且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为
且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为 ,
, ,
, 与
与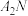 相交于点Q,求证:点Q在某条定直线上.
相交于点Q,求证:点Q在某条定直线上.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,一个焦点为
,一个焦点为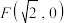 ,P是椭圆上一动点(与左、右顶点不重合).已知
,P是椭圆上一动点(与左、右顶点不重合).已知 的面积的最大值为2.
的面积的最大值为2.(1)求椭圆C的方程;
(2)过点
 且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为
且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为 ,
, ,
, 与
与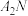 相交于点Q,求证:点Q在某条定直线上.
相交于点Q,求证:点Q在某条定直线上.
您最近一年使用:0次
名校
5 . 已知椭圆 的离心率为
的离心率为 ,点
,点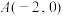 在C上.
在C上.
(1)求椭圆C的方程;
(2)过点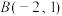 且斜率为
且斜率为 的直线交椭圆C于
的直线交椭圆C于 ,
,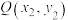 两点,试用含
两点,试用含 的代数式表示
的代数式表示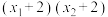 ;
;
(3)在(2)的条件下,过点P作垂直于x轴的直线与直线AQ相交于点M,证明:线段PM的中点在定直线上.
 的离心率为
的离心率为 ,点
,点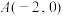 在C上.
在C上.(1)求椭圆C的方程;
(2)过点
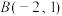 且斜率为
且斜率为 的直线交椭圆C于
的直线交椭圆C于 ,
,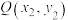 两点,试用含
两点,试用含 的代数式表示
的代数式表示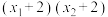 ;
;(3)在(2)的条件下,过点P作垂直于x轴的直线与直线AQ相交于点M,证明:线段PM的中点在定直线上.
您最近一年使用:0次
名校
6 . 给定正整数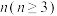 ,集合
,集合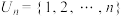 .若存在集合
.若存在集合 ,
, ,
, ,同时满足下列三个条件:
,同时满足下列三个条件:
①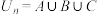 ,
,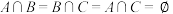 ;
;
②集合 中的元素都为奇数,集合
中的元素都为奇数,集合 中的元素都为偶数,所有能被3整除的数都在集合
中的元素都为偶数,所有能被3整除的数都在集合 中(集合
中(集合 中还可以包含其它数);
中还可以包含其它数);
③集合 ,
, ,
, 中各元素之和分别为
中各元素之和分别为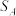 ,
,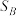 ,
,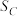 ,有
,有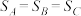 ;
;
则称集合 为可分集合.
为可分集合.
(1)已知 为可分集合,写出相应的一组满足条件的集合
为可分集合,写出相应的一组满足条件的集合 ,
, ,
, ;
;
(2)当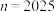 时,
时, 是不是可分集合?判断并说明理由;
是不是可分集合?判断并说明理由;
(3)已知 为偶数,求证:“
为偶数,求证:“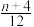 是整数”是“
是整数”是“ 为可分集合”的必要不充分条件.
为可分集合”的必要不充分条件.
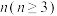 ,集合
,集合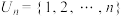 .若存在集合
.若存在集合 ,
, ,
, ,同时满足下列三个条件:
,同时满足下列三个条件:①
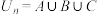 ,
,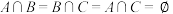 ;
;②集合
 中的元素都为奇数,集合
中的元素都为奇数,集合 中的元素都为偶数,所有能被3整除的数都在集合
中的元素都为偶数,所有能被3整除的数都在集合 中(集合
中(集合 中还可以包含其它数);
中还可以包含其它数);③集合
 ,
, ,
, 中各元素之和分别为
中各元素之和分别为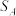 ,
,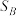 ,
,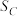 ,有
,有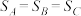 ;
;则称集合
 为可分集合.
为可分集合.(1)已知
 为可分集合,写出相应的一组满足条件的集合
为可分集合,写出相应的一组满足条件的集合 ,
, ,
, ;
;(2)当
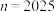 时,
时, 是不是可分集合?判断并说明理由;
是不是可分集合?判断并说明理由;(3)已知
 为偶数,求证:“
为偶数,求证:“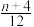 是整数”是“
是整数”是“ 为可分集合”的必要不充分条件.
为可分集合”的必要不充分条件.
您最近一年使用:0次
2024-09-22更新
|
272次组卷
|
3卷引用:北京市顺义牛栏山第一中学2024-2025学年高三上学期月考数学试卷
解题方法
7 . 已知数列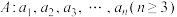 的各项均为正整数,设集合
的各项均为正整数,设集合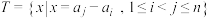 ,记
,记 的元素个数为
的元素个数为 .
.
(1)若数列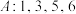 ,求集合
,求集合 ,并写出
,并写出 的值;
的值;
(2)若 是递减数列,求证:“
是递减数列,求证:“ 为等差数列”的充要条件是“
为等差数列”的充要条件是“ ”;
”;
(3)已知数列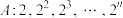 ,求证:
,求证: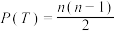 .
.
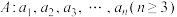 的各项均为正整数,设集合
的各项均为正整数,设集合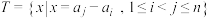 ,记
,记 的元素个数为
的元素个数为 .
.(1)若数列
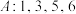 ,求集合
,求集合 ,并写出
,并写出 的值;
的值;(2)若
 是递减数列,求证:“
是递减数列,求证:“ 为等差数列”的充要条件是“
为等差数列”的充要条件是“ ”;
”;(3)已知数列
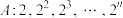 ,求证:
,求证: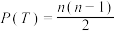 .
.
您最近一年使用:0次
名校
8 . 已知椭圆 的右焦点
的右焦点 坐标为
坐标为 ,两个焦点与短轴一个端点构成等边三角形.
,两个焦点与短轴一个端点构成等边三角形.
(1)求椭圆 的方程和离心率;
的方程和离心率;
(2)若过点 与点
与点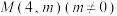 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点,过点
两点,过点 且与直线
且与直线 平行的直线交
平行的直线交 轴于点
轴于点 ,直线
,直线 与直线
与直线 于点
于点 ,求
,求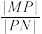 的值.
的值.
 的右焦点
的右焦点 坐标为
坐标为 ,两个焦点与短轴一个端点构成等边三角形.
,两个焦点与短轴一个端点构成等边三角形.(1)求椭圆
 的方程和离心率;
的方程和离心率;(2)若过点
 与点
与点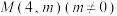 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点,过点
两点,过点 且与直线
且与直线 平行的直线交
平行的直线交 轴于点
轴于点 ,直线
,直线 与直线
与直线 于点
于点 ,求
,求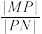 的值.
的值.
您最近一年使用:0次
名校
解题方法
9 . 已知椭圆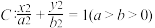 的离心率为
的离心率为 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形的周长为8.
的四个顶点为顶点的四边形的周长为8.
(1)求椭圆 的方程;
的方程;
(2)设直线 是圆
是圆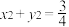 的一条切线,且直线
的一条切线,且直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 的最大值.
的最大值.
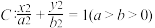 的离心率为
的离心率为 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形的周长为8.
的四个顶点为顶点的四边形的周长为8.(1)求椭圆
 的方程;
的方程;(2)设直线
 是圆
是圆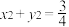 的一条切线,且直线
的一条切线,且直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 的最大值.
的最大值.
您最近一年使用:0次
10 . 已知椭圆C的标准方程为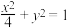 ,梯形
,梯形 的顶点在椭圆上.
的顶点在椭圆上.
(1)已知梯形 的两腰
的两腰 ,且两个底边
,且两个底边 和
和 与坐标轴平行或在坐标轴上.若梯形一底边
与坐标轴平行或在坐标轴上.若梯形一底边 ,高为
,高为 ,求梯形
,求梯形 的面积;
的面积;
(2)若梯形 的两底
的两底 和
和 与坐标轴不平行且不在坐标轴上,判断该梯形是否可以为等腰梯形?并说明理由.
与坐标轴不平行且不在坐标轴上,判断该梯形是否可以为等腰梯形?并说明理由.
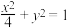 ,梯形
,梯形 的顶点在椭圆上.
的顶点在椭圆上.(1)已知梯形
 的两腰
的两腰 ,且两个底边
,且两个底边 和
和 与坐标轴平行或在坐标轴上.若梯形一底边
与坐标轴平行或在坐标轴上.若梯形一底边 ,高为
,高为 ,求梯形
,求梯形 的面积;
的面积;(2)若梯形
 的两底
的两底 和
和 与坐标轴不平行且不在坐标轴上,判断该梯形是否可以为等腰梯形?并说明理由.
与坐标轴不平行且不在坐标轴上,判断该梯形是否可以为等腰梯形?并说明理由.
您最近一年使用:0次
2024-06-15更新
|
216次组卷
|
2卷引用:北京市十一学校2024届高三下学期三模数学试题



