名校
解题方法
1 . 若一个椭圆的焦距为质数,且离心率的倒数也为质数,则称这样的椭圆为“质朴椭圆”.
(1)证明:椭圆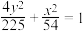 为“质朴椭圆”.
为“质朴椭圆”.
(2)是否存在实数 ,使得椭圆
,使得椭圆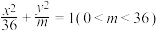 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)设斜率为 的直线
的直线 经过椭圆
经过椭圆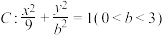 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,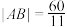 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
(1)证明:椭圆
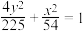 为“质朴椭圆”.
为“质朴椭圆”.(2)是否存在实数
 ,使得椭圆
,使得椭圆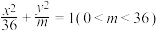 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.(3)设斜率为
 的直线
的直线 经过椭圆
经过椭圆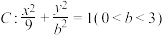 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,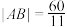 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
您最近一年使用:0次
名校
解题方法
2 . 已知双曲线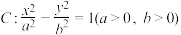 的两条渐近线方程为
的两条渐近线方程为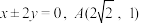 为
为 上一点.
上一点.
(1)求双曲线 的方程;
的方程;
(2)若过点 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;
(3)过双曲线 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于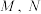 两点,记
两点,记 的中点
的中点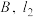 与
与 交于
交于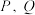 两点,记
两点,记 的中点为
的中点为 .若
.若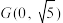 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
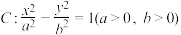 的两条渐近线方程为
的两条渐近线方程为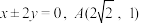 为
为 上一点.
上一点.(1)求双曲线
 的方程;
的方程;(2)若过点
 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;(3)过双曲线
 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于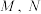 两点,记
两点,记 的中点
的中点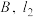 与
与 交于
交于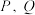 两点,记
两点,记 的中点为
的中点为 .若
.若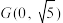 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
您最近一年使用:0次
3 . 已知 为坐标原点,动点
为坐标原点,动点 到
到 轴的距离为
轴的距离为 ,且
,且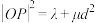 ,其中
,其中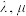 均为常数,动点
均为常数,动点 的轨迹称为
的轨迹称为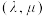 曲线.
曲线.
(1)若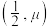 曲线为焦点在
曲线为焦点在 轴上的椭圆,求
轴上的椭圆,求 的取值范围.
的取值范围.
(2)设曲线 为
为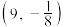 曲线,斜率为
曲线,斜率为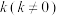 的直线
的直线 过
过 的右焦点,且与
的右焦点,且与 交于
交于 两个不同的点.
两个不同的点.
(i)若 ,求
,求 ;
;
(ii)若点 关于
关于 轴的对称点为点
轴的对称点为点 ,证明:直线
,证明:直线 过定点.
过定点.
 为坐标原点,动点
为坐标原点,动点 到
到 轴的距离为
轴的距离为 ,且
,且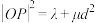 ,其中
,其中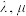 均为常数,动点
均为常数,动点 的轨迹称为
的轨迹称为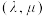 曲线.
曲线.(1)若
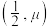 曲线为焦点在
曲线为焦点在 轴上的椭圆,求
轴上的椭圆,求 的取值范围.
的取值范围.(2)设曲线
 为
为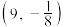 曲线,斜率为
曲线,斜率为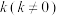 的直线
的直线 过
过 的右焦点,且与
的右焦点,且与 交于
交于 两个不同的点.
两个不同的点.(i)若
 ,求
,求 ;
;(ii)若点
 关于
关于 轴的对称点为点
轴的对称点为点 ,证明:直线
,证明:直线 过定点.
过定点.
您最近一年使用:0次
解题方法
4 . 已知集合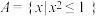 ,
,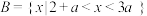
(1)若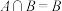 ,实数
,实数 的取值范围;
的取值范围;
(2)若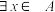 ,
, 是假命题,求实数
是假命题,求实数 的取值集合
的取值集合 ;
;
(3)设不等式 的解集为D,若
的解集为D,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
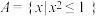 ,
,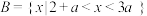
(1)若
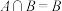 ,实数
,实数 的取值范围;
的取值范围;(2)若
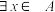 ,
, 是假命题,求实数
是假命题,求实数 的取值集合
的取值集合 ;
;(3)设不等式
 的解集为D,若
的解集为D,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
5 . 已知 是R的非空真子集,如果对任意
是R的非空真子集,如果对任意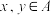 ,都有
,都有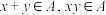 ,则称
,则称 是封闭集.
是封闭集.
(1)判断集合 是否为封闭集,并说明理由;
是否为封闭集,并说明理由;
(2)判断以下两个命题的真假,并说明理由;
命题 :若非空集合
:若非空集合 是封闭集,则
是封闭集,则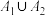 也是封闭集;
也是封闭集;
命题 :非空集合
:非空集合 是封闭集,则
是封闭集,则 是
是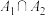 是封闭集的充要条件;
是封闭集的充要条件;
(3)若非空集合 是封闭集合,设全集为R,求证:A的补集不是封闭集
是封闭集合,设全集为R,求证:A的补集不是封闭集
 是R的非空真子集,如果对任意
是R的非空真子集,如果对任意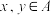 ,都有
,都有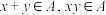 ,则称
,则称 是封闭集.
是封闭集.(1)判断集合
 是否为封闭集,并说明理由;
是否为封闭集,并说明理由;(2)判断以下两个命题的真假,并说明理由;
命题
 :若非空集合
:若非空集合 是封闭集,则
是封闭集,则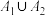 也是封闭集;
也是封闭集;命题
 :非空集合
:非空集合 是封闭集,则
是封闭集,则 是
是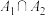 是封闭集的充要条件;
是封闭集的充要条件;(3)若非空集合
 是封闭集合,设全集为R,求证:A的补集不是封闭集
是封闭集合,设全集为R,求证:A的补集不是封闭集
您最近一年使用:0次
2024-10-15更新
|
597次组卷
|
3卷引用:广西南宁市北京大学南宁附属实验学校2024-2025学年高一上学期9月月考数学试卷
名校
解题方法
6 . 已知平面内一动点 到点
到点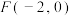 的距离与点
的距离与点 到定直线
到定直线 的距离之比为
的距离之比为 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程.
的方程.
(2)在直线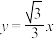 上有一点
上有一点 ,过点
,过点 的直线
的直线 与曲线
与曲线 相交于
相交于 两点.设
两点.设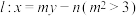 ,证明:
,证明: 只与
只与 有关.
有关.
 到点
到点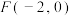 的距离与点
的距离与点 到定直线
到定直线 的距离之比为
的距离之比为 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程.
的方程.(2)在直线
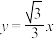 上有一点
上有一点 ,过点
,过点 的直线
的直线 与曲线
与曲线 相交于
相交于 两点.设
两点.设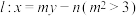 ,证明:
,证明: 只与
只与 有关.
有关.
您最近一年使用:0次
2024-09-13更新
|
349次组卷
|
2卷引用:广西桂平市部分示范性高中2025届高三开学摸底考试数学试卷
7 . 已知抛物线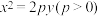 的焦点为
的焦点为 ,过圆
,过圆 的圆心的直线交抛物线与圆分别为
的圆心的直线交抛物线与圆分别为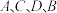 (从左到右).
(从左到右).
(2)若抛物线和圆只有一个公共点,求 的取值范围;
的取值范围;
(3)在(1)的条件下,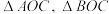 的面积满足:
的面积满足: ,求弦
,求弦 的长.
的长.
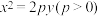 的焦点为
的焦点为 ,过圆
,过圆 的圆心的直线交抛物线与圆分别为
的圆心的直线交抛物线与圆分别为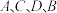 (从左到右).
(从左到右).
(2)若抛物线和圆只有一个公共点,求
 的取值范围;
的取值范围;(3)在(1)的条件下,
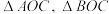 的面积满足:
的面积满足: ,求弦
,求弦 的长.
的长.
您最近一年使用:0次
2024-09-08更新
|
522次组卷
|
2卷引用:广西柳州铁一中学2024-2025 学年高二上学期9月月考数学试题
名校
8 . 如下图,在 中,
中,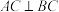 ,
,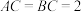 ,D是AC中点,E、F分别是BA、BC边上的动点,且
,D是AC中点,E、F分别是BA、BC边上的动点,且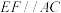 ;将
;将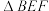 沿EF折起,将点B折至点P的位置,得到四棱锥;
沿EF折起,将点B折至点P的位置,得到四棱锥; ;
;
(2)若 ,二面角
,二面角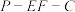 是直二面角,求二面角
是直二面角,求二面角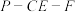 的正切值;
的正切值;
(3)当 时,求直线PE与平面ABC所成角的正弦值的取值范围.
时,求直线PE与平面ABC所成角的正弦值的取值范围.
 中,
中,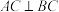 ,
,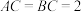 ,D是AC中点,E、F分别是BA、BC边上的动点,且
,D是AC中点,E、F分别是BA、BC边上的动点,且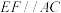 ;将
;将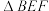 沿EF折起,将点B折至点P的位置,得到四棱锥;
沿EF折起,将点B折至点P的位置,得到四棱锥; 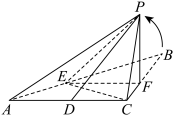
 ;
;(2)若
 ,二面角
,二面角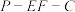 是直二面角,求二面角
是直二面角,求二面角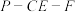 的正切值;
的正切值;(3)当
 时,求直线PE与平面ABC所成角的正弦值的取值范围.
时,求直线PE与平面ABC所成角的正弦值的取值范围.
您最近一年使用:0次
2024-08-29更新
|
2353次组卷
|
8卷引用:广西南宁市第三中五象校区学2024-2025学年高二上学期月考数学试题(一)
广西南宁市第三中五象校区学2024-2025学年高二上学期月考数学试题(一)黑龙江省哈尔滨市第九中学校2024-2025学年高二上学期八月学业阶段性评价考试数学试卷(已下线)微点4 空间向量的应用【练】(高中同步进阶微专题)(已下线)四川省成都市第七中学2024-2025学年高二上学期10月测试数学试题河南省开封市龙亭区河南大学附属中学2024-2025学年高二上学期10月月考数学试题重庆市第二十九中学2024-2025学年高二上学期第1次月考数学试题河南省新乡市河南师范大学附属中学2024-2025学年高二上学期10月月考数学试卷广东省广州市第五中学2024-2025学年高二上学期第一次段考数学试卷
解题方法
9 . 已知椭圆C: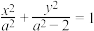 过定点
过定点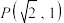 ,过点
,过点 的两条动直线交椭圆于
的两条动直线交椭圆于 ,直线
,直线 的倾斜角互补,
的倾斜角互补, 为椭圆C的右焦点.
为椭圆C的右焦点. 是椭圆
是椭圆 的动点,过点
的动点,过点 作直线
作直线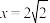 的垂线
的垂线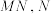 为垂足,求
为垂足,求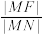 .
.
(2)在 中,记
中,记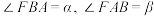 ,若直线AB的斜率为
,若直线AB的斜率为 ,求
,求 的最大值.
的最大值.
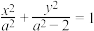 过定点
过定点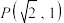 ,过点
,过点 的两条动直线交椭圆于
的两条动直线交椭圆于 ,直线
,直线 的倾斜角互补,
的倾斜角互补, 为椭圆C的右焦点.
为椭圆C的右焦点.
 是椭圆
是椭圆 的动点,过点
的动点,过点 作直线
作直线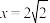 的垂线
的垂线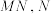 为垂足,求
为垂足,求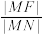 .
.(2)在
 中,记
中,记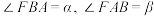 ,若直线AB的斜率为
,若直线AB的斜率为 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线 的两条渐近线分别为
的两条渐近线分别为 和
和 ,右焦点坐标为
,右焦点坐标为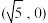 ,
, 为坐标原点.
为坐标原点.
(2)设M,N是双曲线C上不同的两点,Q是MN的中点,直线MN、OQ的斜率分别为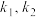 ,证明:
,证明: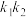 为定值;
为定值;
(3)直线y=4x-6与双曲线的右支交于点 (
(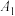 在
在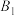 的上方),过点
的上方),过点 分别作
分别作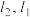 的平行线,交于点
的平行线,交于点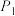 ,过点
,过点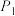 且斜率为4的直线与双曲线交于点
且斜率为4的直线与双曲线交于点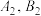 (
(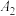 在
在 的上方),再过点
的上方),再过点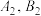 分别作
分别作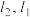 的平行线,交于点
的平行线,交于点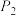 ,⋯,这样一直操作下去,可以得到一列点
,⋯,这样一直操作下去,可以得到一列点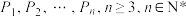 .证明:
.证明: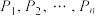 共线.
共线.
 的两条渐近线分别为
的两条渐近线分别为 和
和 ,右焦点坐标为
,右焦点坐标为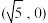 ,
, 为坐标原点.
为坐标原点.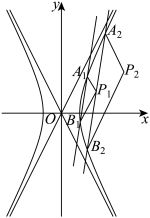
(2)设M,N是双曲线C上不同的两点,Q是MN的中点,直线MN、OQ的斜率分别为
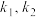 ,证明:
,证明: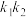 为定值;
为定值;(3)直线y=4x-6与双曲线的右支交于点
 (
(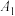 在
在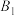 的上方),过点
的上方),过点 分别作
分别作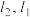 的平行线,交于点
的平行线,交于点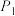 ,过点
,过点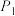 且斜率为4的直线与双曲线交于点
且斜率为4的直线与双曲线交于点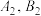 (
(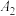 在
在 的上方),再过点
的上方),再过点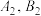 分别作
分别作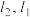 的平行线,交于点
的平行线,交于点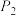 ,⋯,这样一直操作下去,可以得到一列点
,⋯,这样一直操作下去,可以得到一列点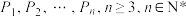 .证明:
.证明: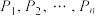 共线.
共线.
您最近一年使用:0次
2024-07-31更新
|
420次组卷
|
3卷引用:广西壮族自治区“贵百河—武鸣高中”2025届高三上学期9月摸底考试数学试题



