1 . 在平面直角坐标系 中,点
中,点 到点
到点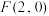 的距离与到直线
的距离与到直线 的距离之比为
的距离之比为 ,记
,记 的轨迹为曲线
的轨迹为曲线 ,直线
,直线 交
交 右支于
右支于 ,
, 两点,直线
两点,直线 交
交 右支于
右支于 ,
, 两点,
两点,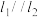 .
.
(1)求 的标准方程;
的标准方程;
(2)证明: ;
;
(3)若直线 过点
过点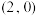 ,直线
,直线 过点
过点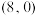 ,记
,记 ,
, 的中点分别为
的中点分别为 ,
, ,过点
,过点 作
作 两条渐近线的垂线,垂足分别为
两条渐近线的垂线,垂足分别为 ,
, ,求四边形
,求四边形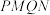 面积的取值范围.
面积的取值范围.
 中,点
中,点 到点
到点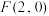 的距离与到直线
的距离与到直线 的距离之比为
的距离之比为 ,记
,记 的轨迹为曲线
的轨迹为曲线 ,直线
,直线 交
交 右支于
右支于 ,
, 两点,直线
两点,直线 交
交 右支于
右支于 ,
, 两点,
两点,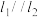 .
.(1)求
 的标准方程;
的标准方程;(2)证明:
 ;
;(3)若直线
 过点
过点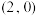 ,直线
,直线 过点
过点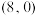 ,记
,记 ,
, 的中点分别为
的中点分别为 ,
, ,过点
,过点 作
作 两条渐近线的垂线,垂足分别为
两条渐近线的垂线,垂足分别为 ,
, ,求四边形
,求四边形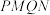 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
2024-07-26更新
|
1086次组卷
|
5卷引用:广东省广州市2025届普通高中毕业班摸底考试数学试题
广东省广州市2025届普通高中毕业班摸底考试数学试题福建省厦门双十中学2024届高三第一次模拟考试数学试题(已下线)重难点突破17 圆锥曲线中参数范围与最值问题(八大题型)(已下线)重难点突破07 圆锥曲线三角形面积与四边形面积题型归类(七大题型)(已下线)第03节 解析几何中函数与方程思想【练】高三数学思想大全
名校
解题方法
2 . 如图,在三棱柱 中,底面是边长为2的等边三角形,
中,底面是边长为2的等边三角形, ,D,E分别是线段
,D,E分别是线段 ,
, 的中点,
的中点, 在平面ABC内的射影为
在平面ABC内的射影为 .
.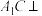 平面BDE;
平面BDE;
(2)若点F为棱 的中点,求点
的中点,求点 到平面BDE的距离;
到平面BDE的距离;
(3)若点F为线段 上的动点(不包括端点),求平面FBD与平面BDE夹角的余弦值的取值范围.
上的动点(不包括端点),求平面FBD与平面BDE夹角的余弦值的取值范围.
 中,底面是边长为2的等边三角形,
中,底面是边长为2的等边三角形, ,D,E分别是线段
,D,E分别是线段 ,
, 的中点,
的中点, 在平面ABC内的射影为
在平面ABC内的射影为 .
.
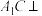 平面BDE;
平面BDE;(2)若点F为棱
 的中点,求点
的中点,求点 到平面BDE的距离;
到平面BDE的距离;(3)若点F为线段
 上的动点(不包括端点),求平面FBD与平面BDE夹角的余弦值的取值范围.
上的动点(不包括端点),求平面FBD与平面BDE夹角的余弦值的取值范围.
您最近一年使用:0次
7日内更新
|
691次组卷
|
3卷引用:广东省湛江市雷州市第二中学2024-2025学年高二上学期10月月考数学试题
3 . 已知椭圆 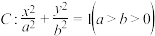 的左、右焦点分别为
的左、右焦点分别为 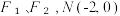 为椭圆的一个顶点,且右焦点 F₂到双曲线.
为椭圆的一个顶点,且右焦点 F₂到双曲线. 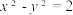 渐近线的距离为
渐近线的距离为 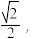
(1)求椭圆C的标准方程;
(2)设直线 与椭圆C交于 A、B两点.
与椭圆C交于 A、B两点.
①若直线 过椭圆右焦点F₂,且△AF₁B的面积为
过椭圆右焦点F₂,且△AF₁B的面积为 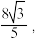 求实数k的值;
求实数k的值;
②若直线 过定点P(0,2), 且k>0, 在x轴上是否存在点T(t,0)使得以TA、TB为邻边的平行四边形为菱形? 若存在,则求出实数t的取值范围; 若不存在,请说明理由.
过定点P(0,2), 且k>0, 在x轴上是否存在点T(t,0)使得以TA、TB为邻边的平行四边形为菱形? 若存在,则求出实数t的取值范围; 若不存在,请说明理由.
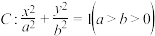 的左、右焦点分别为
的左、右焦点分别为 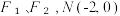 为椭圆的一个顶点,且右焦点 F₂到双曲线.
为椭圆的一个顶点,且右焦点 F₂到双曲线. 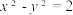 渐近线的距离为
渐近线的距离为 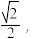
(1)求椭圆C的标准方程;
(2)设直线
 与椭圆C交于 A、B两点.
与椭圆C交于 A、B两点.①若直线
 过椭圆右焦点F₂,且△AF₁B的面积为
过椭圆右焦点F₂,且△AF₁B的面积为 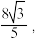 求实数k的值;
求实数k的值;②若直线
 过定点P(0,2), 且k>0, 在x轴上是否存在点T(t,0)使得以TA、TB为邻边的平行四边形为菱形? 若存在,则求出实数t的取值范围; 若不存在,请说明理由.
过定点P(0,2), 且k>0, 在x轴上是否存在点T(t,0)使得以TA、TB为邻边的平行四边形为菱形? 若存在,则求出实数t的取值范围; 若不存在,请说明理由.
您最近一年使用:0次
2024-10-25更新
|
759次组卷
|
3卷引用:广东省广州市执信中学2025届高三上学期第四次测试数学试题
4 . 已知双曲线 的实轴长为4,渐近线方程为
的实轴长为4,渐近线方程为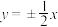 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)双曲线的左、右顶点分别为 ,过点
,过点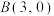 作与
作与 轴不重合的直线
轴不重合的直线 与
与 交于
交于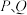 两点,直线
两点,直线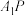 与
与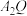 交于点S,直线
交于点S,直线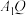 与
与 交于点
交于点 .
.
(i)设直线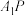 的斜率为
的斜率为 ,直线
,直线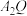 的斜率为
的斜率为 ,若
,若 ,求
,求 的值;
的值;
(ii)求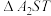 的面积的取值范围.
的面积的取值范围.
 的实轴长为4,渐近线方程为
的实轴长为4,渐近线方程为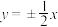 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)双曲线的左、右顶点分别为
 ,过点
,过点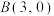 作与
作与 轴不重合的直线
轴不重合的直线 与
与 交于
交于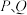 两点,直线
两点,直线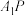 与
与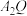 交于点S,直线
交于点S,直线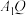 与
与 交于点
交于点 .
.(i)设直线
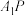 的斜率为
的斜率为 ,直线
,直线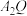 的斜率为
的斜率为 ,若
,若 ,求
,求 的值;
的值;(ii)求
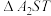 的面积的取值范围.
的面积的取值范围.
您最近一年使用:0次
2024-10-24更新
|
767次组卷
|
4卷引用:广东省七校2025届高三上学期第二次联考数学试卷
名校
解题方法
5 . 已知椭圆 :
: 的离心率为
的离心率为 ,右顶点
,右顶点 与
与 的上,下顶点所围成的三角形面积为
的上,下顶点所围成的三角形面积为 .
.
(1)求 的方程;
的方程;
(2)不过点 的动直线
的动直线 与
与 交于
交于 ,
, 两点,直线
两点,直线 与
与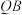 的斜率之积恒为
的斜率之积恒为 ,证明直线
,证明直线 过定点,并求出这个定点.
过定点,并求出这个定点.
 :
: 的离心率为
的离心率为 ,右顶点
,右顶点 与
与 的上,下顶点所围成的三角形面积为
的上,下顶点所围成的三角形面积为 .
.(1)求
 的方程;
的方程;(2)不过点
 的动直线
的动直线 与
与 交于
交于 ,
, 两点,直线
两点,直线 与
与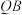 的斜率之积恒为
的斜率之积恒为 ,证明直线
,证明直线 过定点,并求出这个定点.
过定点,并求出这个定点.
您最近一年使用:0次
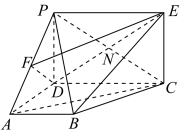
6 . 如图所示的几何体中,四边形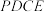 为矩形,在梯形
为矩形,在梯形 中,
中,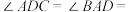
 ,
, 为
为 的中点,
的中点,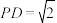 ,
,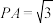 ,
,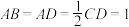 ,线段
,线段 交
交 于点
于点 .
.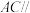 平面
平面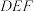 ;
;
(2)求二面角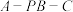 的正弦值;
的正弦值;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面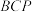 所成角的大小为
所成角的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
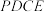 为矩形,在梯形
为矩形,在梯形 中,
中,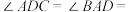
 ,
, 为
为 的中点,
的中点, ,
,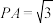 ,
,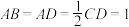 ,线段
,线段 交
交 于点
于点 .
.
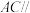 平面
平面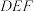 ;
;(2)求二面角
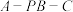 的正弦值;
的正弦值;(3)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面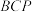 所成角的大小为
所成角的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
您最近一年使用:0次
7 . 已知椭圆 的离心率为
的离心率为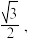 点
点 在椭圆
在椭圆 上运动,且
上运动,且 面积的最大值为
面积的最大值为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 分别是椭圆
分别是椭圆 的右顶点和上顶点,直线
的右顶点和上顶点,直线 与直线
与直线 平行,且与
平行,且与 轴,
轴, 轴分别交于点
轴分别交于点 ,与椭圆
,与椭圆 相交于点
相交于点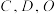 为坐标原点.
为坐标原点.
(i)求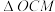 与
与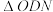 的面积之比;
的面积之比;
(ii)证明: 为定值.
为定值.
 的离心率为
的离心率为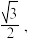 点
点 在椭圆
在椭圆 上运动,且
上运动,且 面积的最大值为
面积的最大值为 .
.(1)求椭圆
 的方程;
的方程;(2)设
 分别是椭圆
分别是椭圆 的右顶点和上顶点,直线
的右顶点和上顶点,直线 与直线
与直线 平行,且与
平行,且与 轴,
轴, 轴分别交于点
轴分别交于点 ,与椭圆
,与椭圆 相交于点
相交于点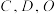 为坐标原点.
为坐标原点.(i)求
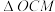 与
与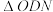 的面积之比;
的面积之比;(ii)证明:
 为定值.
为定值.
您最近一年使用:0次
2024-10-15更新
|
611次组卷
|
4卷引用:广东省潮州市饶平县2025届高三上学期第二次质量检测数学试题
广东省潮州市饶平县2025届高三上学期第二次质量检测数学试题青海省西宁市大通回族土族自治县2024-2025学年高三上学期开学摸底考试数学试题新疆维吾尔自治区喀什第二中学2025届高三上学期9月月考数学试题(已下线)3.1.2 椭圆的简单几何性质——课后作业(巩固版)
解题方法
8 . 已知椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 ,直线
,直线 经过点
经过点 ,且与
,且与 相交于
相交于 ,
, 两点,记
两点,记 的倾斜角为
的倾斜角为 .
.
(1)求 的方程;
的方程;
(2)求弦 的长(用
的长(用 表示);
表示);
(3)若直线 也经过点
也经过点 ,且倾斜角比
,且倾斜角比 的倾斜角大
的倾斜角大 ,求四边形
,求四边形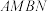 面积的最小值.
面积的最小值.
 的右焦点为
的右焦点为 ,离心率为
,离心率为 ,直线
,直线 经过点
经过点 ,且与
,且与 相交于
相交于 ,
, 两点,记
两点,记 的倾斜角为
的倾斜角为 .
.(1)求
 的方程;
的方程;(2)求弦
 的长(用
的长(用 表示);
表示);(3)若直线
 也经过点
也经过点 ,且倾斜角比
,且倾斜角比 的倾斜角大
的倾斜角大 ,求四边形
,求四边形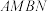 面积的最小值.
面积的最小值.
您最近一年使用:0次
2024-10-13更新
|
448次组卷
|
5卷引用:广东省揭阳市2024-2025学年高三上学期9月月考数学试题
9 . 如图,四棱锥 的底面是矩形,
的底面是矩形, 底面
底面 ,
,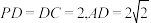 ,M为
,M为 的中点.
的中点.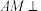 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
 的底面是矩形,
的底面是矩形, 底面
底面 ,
,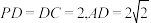 ,M为
,M为 的中点.
的中点.
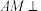 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正切值.
所成角的正切值.
您最近一年使用:0次
10 . 已知双曲线 的右焦点
的右焦点 到其中一条渐近线
到其中一条渐近线 的距离为
的距离为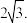
(1)求 的标准方程;
的标准方程;
(2)若过 的直线与
的直线与 的左、右支分别交于点
的左、右支分别交于点 ,与圆
,与圆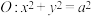 交于与
交于与 不重合的
不重合的 两点.
两点.
①求直线 斜率的取值范围;
斜率的取值范围;
②求 的取值范围.
的取值范围.
 的右焦点
的右焦点 到其中一条渐近线
到其中一条渐近线 的距离为
的距离为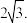
(1)求
 的标准方程;
的标准方程;(2)若过
 的直线与
的直线与 的左、右支分别交于点
的左、右支分别交于点 ,与圆
,与圆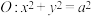 交于与
交于与 不重合的
不重合的 两点.
两点.①求直线
 斜率的取值范围;
斜率的取值范围;②求
 的取值范围.
的取值范围.
您最近一年使用:0次



