名校
解题方法
1 . 已知离心率为 的椭圆
的椭圆 的右焦点为
的右焦点为 ,点
,点 为椭圆上第一象限内的一点,满足
为椭圆上第一象限内的一点,满足 垂直于
垂直于 轴,且
轴,且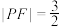 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 的斜率存在,交椭圆
的斜率存在,交椭圆 于
于 两点,
两点, 三点不共线,且直线
三点不共线,且直线 和直线
和直线 关于直线
关于直线 对称,证明:直线
对称,证明:直线 过定点.
过定点.
 的椭圆
的椭圆 的右焦点为
的右焦点为 ,点
,点 为椭圆上第一象限内的一点,满足
为椭圆上第一象限内的一点,满足 垂直于
垂直于 轴,且
轴,且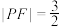 .
.(1)求椭圆
 的方程;
的方程;(2)直线
 的斜率存在,交椭圆
的斜率存在,交椭圆 于
于 两点,
两点, 三点不共线,且直线
三点不共线,且直线 和直线
和直线 关于直线
关于直线 对称,证明:直线
对称,证明:直线 过定点.
过定点.
您最近一年使用:0次
名校
解题方法
2 . 已知双曲线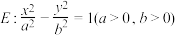 的右焦点为F,左、右顶点分别为M,N,点
的右焦点为F,左、右顶点分别为M,N,点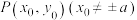 是E上一点,且直线PM,PN的斜率之积为
是E上一点,且直线PM,PN的斜率之积为 .
.
(1)求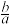 的值;
的值;
(2)过F且斜率为1的直线l交E于A,B两点,O为坐标原点,C为E上一点,满足 ,
, 的面积为
的面积为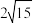 ,求E的方程.
,求E的方程.
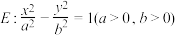 的右焦点为F,左、右顶点分别为M,N,点
的右焦点为F,左、右顶点分别为M,N,点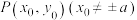 是E上一点,且直线PM,PN的斜率之积为
是E上一点,且直线PM,PN的斜率之积为 .
.(1)求
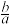 的值;
的值;(2)过F且斜率为1的直线l交E于A,B两点,O为坐标原点,C为E上一点,满足
 ,
, 的面积为
的面积为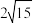 ,求E的方程.
,求E的方程.
您最近一年使用:0次
2024-05-12更新
|
378次组卷
|
3卷引用:甘肃省武威第六中学2023-2024学年高三下学期第五次诊断数学试卷
3 . 在平面直角坐标系 中,动点
中,动点 (
( )与定点
)与定点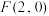 的距离和
的距离和 到直线
到直线 :
: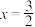 的距离之比是常数
的距离之比是常数 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)记动点 的轨迹为曲线
的轨迹为曲线 ,过点
,过点 的直线
的直线 与曲线
与曲线 交于
交于 两点,直线
两点,直线 与曲线
与曲线 的另一个交点为
的另一个交点为 .
.
(i)求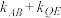 的值;
的值;
(ii)记 面积为
面积为 ,
,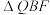 面积为
面积为 ,
, 面积为
面积为 ,试问
,试问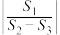 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
 中,动点
中,动点 (
( )与定点
)与定点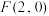 的距离和
的距离和 到直线
到直线 :
: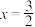 的距离之比是常数
的距离之比是常数 .
.(1)求动点
 的轨迹方程;
的轨迹方程;(2)记动点
 的轨迹为曲线
的轨迹为曲线 ,过点
,过点 的直线
的直线 与曲线
与曲线 交于
交于 两点,直线
两点,直线 与曲线
与曲线 的另一个交点为
的另一个交点为 .
.(i)求
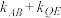 的值;
的值;(ii)记
 面积为
面积为 ,
,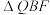 面积为
面积为 ,
, 面积为
面积为 ,试问
,试问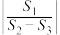 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
您最近一年使用:0次
2024-05-08更新
|
1082次组卷
|
4卷引用:甘肃省兰州市第五十八中学2024届高三第二次高考仿真考试数学试题
甘肃省兰州市第五十八中学2024届高三第二次高考仿真考试数学试题浙江省绍兴市上虞区2023-2024学年高三下学期适应性教学质量调测数学试卷(已下线)专题11 解析几何中的定值问题【练】(压轴大全)贵州省贵州大学附属中学2023-2024学年高二下学期7月期末考试数学试卷
名校
解题方法
4 . 在平面直角坐标系 中,点
中,点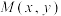 到点
到点 与到直线
与到直线 的距离之比为
的距离之比为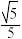 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)若点 是圆
是圆 上的一点(不在坐标轴上),过点
上的一点(不在坐标轴上),过点 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,记直线
,记直线 的斜率分别为
的斜率分别为 ,且
,且 ,求直线
,求直线 的方程.
的方程.
 中,点
中,点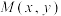 到点
到点 与到直线
与到直线 的距离之比为
的距离之比为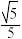 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)若点
 是圆
是圆 上的一点(不在坐标轴上),过点
上的一点(不在坐标轴上),过点 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,记直线
,记直线 的斜率分别为
的斜率分别为 ,且
,且 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-04-13更新
|
297次组卷
|
7卷引用:甘肃省定西市渭源一中教育联盟2025届高三上学期暑假开放日教学测试数学试题
名校
解题方法
5 . 双曲线 上一点
上一点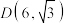 到左、右焦点的距离之差为6,
到左、右焦点的距离之差为6,
(1)求双曲线 的方程,
的方程,
(2)已知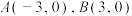 ,过点
,过点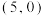 的直线
的直线 与
与 交于
交于 (异于
(异于 )两点,直线
)两点,直线 与
与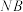 交于点
交于点 ,试问点
,试问点 到直线
到直线 的距离是否为定值?若是,求出该定值;若不是,请说明理由,
的距离是否为定值?若是,求出该定值;若不是,请说明理由,
 上一点
上一点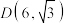 到左、右焦点的距离之差为6,
到左、右焦点的距离之差为6,(1)求双曲线
 的方程,
的方程,(2)已知
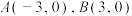 ,过点
,过点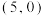 的直线
的直线 与
与 交于
交于 (异于
(异于 )两点,直线
)两点,直线 与
与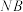 交于点
交于点 ,试问点
,试问点 到直线
到直线 的距离是否为定值?若是,求出该定值;若不是,请说明理由,
的距离是否为定值?若是,求出该定值;若不是,请说明理由,
您最近一年使用:0次
2024-04-12更新
|
2580次组卷
|
8卷引用:甘肃省定西市2023-2024学年高三下学期教学质量统一检测数学试题
名校
解题方法
6 . 已知双曲线  与双曲线
与双曲线  的渐近线相同,且M 经过点
的渐近线相同,且M 经过点 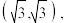
 的焦距为4.
的焦距为4.
(1)求M 和 的方程;
的方程;
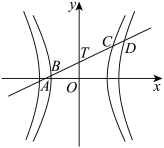
(2)如图,过点 T(0,1)的直线 l(斜率大于0)与双曲线 M 和 N 的左、右两支依次相交于A,B,C,D,若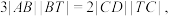 求直线 l的方程.
求直线 l的方程.
 与双曲线
与双曲线  的渐近线相同,且M 经过点
的渐近线相同,且M 经过点 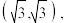
 的焦距为4.
的焦距为4.
(1)求M 和
 的方程;
的方程;(2)如图,过点 T(0,1)的直线 l(斜率大于0)与双曲线 M 和 N 的左、右两支依次相交于A,B,C,D,若
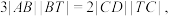 求直线 l的方程.
求直线 l的方程.
您最近一年使用:0次
2024-03-24更新
|
655次组卷
|
2卷引用:甘肃省陇南市部分学校2024届高三一模联考数学试题
7 . 已知椭圆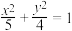 的右焦点为
的右焦点为 ,设直线
,设直线 :
: 与
与 轴的交点为
轴的交点为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 与椭圆交于
与椭圆交于 、
、 两点,
两点, 为线段
为线段 的中点.
的中点.

(1)若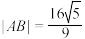 ,求直线
,求直线 的倾斜角;
的倾斜角;
(2)设直线 交直线
交直线 于点
于点 .
.
①求直线 的斜率;
的斜率;
②求 的值.
的值.
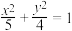 的右焦点为
的右焦点为 ,设直线
,设直线 :
: 与
与 轴的交点为
轴的交点为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 与椭圆交于
与椭圆交于 、
、 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)若
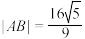 ,求直线
,求直线 的倾斜角;
的倾斜角;(2)设直线
 交直线
交直线 于点
于点 .
.①求直线
 的斜率;
的斜率;②求
 的值.
的值.
您最近一年使用:0次
名校
解题方法
8 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点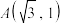 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若椭圆的上顶点为点 ,过点
,过点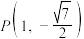 的直线交椭圆于点
的直线交椭圆于点 ,证明:
,证明: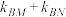 为定值,并求出定值.
为定值,并求出定值.
 的离心率为
的离心率为 ,且过点
,且过点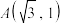 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若椭圆的上顶点为点
 ,过点
,过点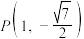 的直线交椭圆于点
的直线交椭圆于点 ,证明:
,证明: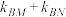 为定值,并求出定值.
为定值,并求出定值.
您最近一年使用:0次
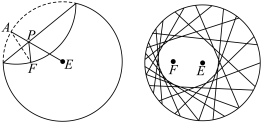
9 . “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图).
步骤2:把纸片折叠,使圆周正好通过点F;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
已知这些折痕所围成的图形是一个椭圆.若取半径为6的圆形纸片,设定点F到圆心E的距离为4,按上述方法折纸.
(1)以点F、E所在的直线为x轴,建立适当的坐标系,求折痕围成的椭圆C的标准方程;
(2)若过点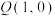 且不与y轴垂直的直线l与椭圆C交于M,N两点,在x轴的正半轴上是否存在定点
且不与y轴垂直的直线l与椭圆C交于M,N两点,在x轴的正半轴上是否存在定点 ,使得直线TM,TN的斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.
,使得直线TM,TN的斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.
步骤2:把纸片折叠,使圆周正好通过点F;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
已知这些折痕所围成的图形是一个椭圆.若取半径为6的圆形纸片,设定点F到圆心E的距离为4,按上述方法折纸.
(1)以点F、E所在的直线为x轴,建立适当的坐标系,求折痕围成的椭圆C的标准方程;
(2)若过点
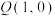 且不与y轴垂直的直线l与椭圆C交于M,N两点,在x轴的正半轴上是否存在定点
且不与y轴垂直的直线l与椭圆C交于M,N两点,在x轴的正半轴上是否存在定点 ,使得直线TM,TN的斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.
,使得直线TM,TN的斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线 的两条渐近线互相垂直,且经过点
的两条渐近线互相垂直,且经过点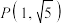 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)若过点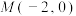 的直线交双曲线同一支于两点
的直线交双曲线同一支于两点 ,设
,设 中点为
中点为 ,求
,求 面积的取值范围.
面积的取值范围.
 的两条渐近线互相垂直,且经过点
的两条渐近线互相垂直,且经过点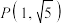 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)若过点
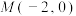 的直线交双曲线同一支于两点
的直线交双曲线同一支于两点 ,设
,设 中点为
中点为 ,求
,求 面积的取值范围.
面积的取值范围.
您最近一年使用:0次



