名校
解题方法
1 . 已知动圆 经过点
经过点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)设过点 且斜率为正的直线
且斜率为正的直线 交曲线
交曲线 于
于 两点(点
两点(点 在点
在点 的上方),
的上方), 的中点为
的中点为 ,
,
①过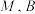 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,试证明:
,试证明: ;
;
②设线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,若
,若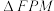 的面积为4,求直线
的面积为4,求直线 的方程.
的方程.
 经过点
经过点 且与直线
且与直线 相切,记圆心
相切,记圆心 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)设过点
 且斜率为正的直线
且斜率为正的直线 交曲线
交曲线 于
于 两点(点
两点(点 在点
在点 的上方),
的上方), 的中点为
的中点为 ,
,①过
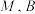 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,试证明:
,试证明: ;
;②设线段
 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,若
,若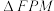 的面积为4,求直线
的面积为4,求直线 的方程.
的方程.
您最近一年使用:0次
2024-10-17更新
|
838次组卷
|
2卷引用:四川省巴中市2025届高三上学期“零诊”考试数学试题
名校
解题方法
2 . 在空间直角坐标系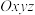 中,过点
中,过点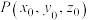 且以
且以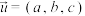 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为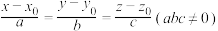 ,过点
,过点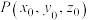 且以
且以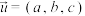 为法向量的平面方程可表示为
为法向量的平面方程可表示为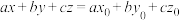 .
.
(1)若直线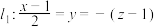 与
与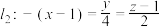 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;
(2)在三棱柱 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面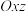 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;
(3)若集合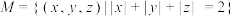 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
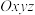 中,过点
中,过点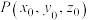 且以
且以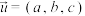 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为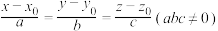 ,过点
,过点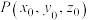 且以
且以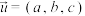 为法向量的平面方程可表示为
为法向量的平面方程可表示为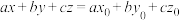 .
.(1)若直线
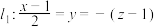 与
与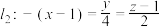 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;(2)在三棱柱
 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面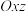 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;(3)若集合
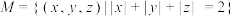 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
您最近一年使用:0次
名校
解题方法
3 . 已知两个非零向量 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
都垂直,它的模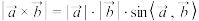 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,
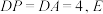 为线段
为线段 上一点,
上一点,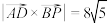 .
. 的长;
的长;
(2)若 为
为 的中点,求二面角
的中点,求二面角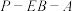 的正弦值;
的正弦值;
(3)若 为线段
为线段 上一点,且满足
上一点,且满足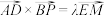 ,求
,求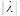 .
.
 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
都垂直,它的模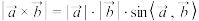 .如图,在四棱锥
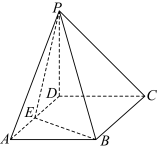
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,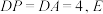 为线段
为线段 上一点,
上一点,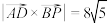 .
.
 的长;
的长;(2)若
 为
为 的中点,求二面角
的中点,求二面角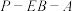 的正弦值;
的正弦值;(3)若
 为线段
为线段 上一点,且满足
上一点,且满足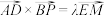 ,求
,求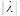 .
.
您最近一年使用:0次
7日内更新
|
473次组卷
|
3卷引用:四川省内江市威远中学校2024-2025学年高二上学期期中考试数学试题
4 . 已知点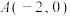 ,
,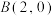 ,点P在以AB为直径的圆C上运动,
,点P在以AB为直径的圆C上运动,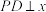 轴,垂足为D,点M满足
轴,垂足为D,点M满足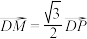 ,点M的轨迹为W,过点
,点M的轨迹为W,过点 的直线l交W于点E、F.
的直线l交W于点E、F.
(1)求W的方程;
(2)若直线l的倾斜角为 ,求直线l被圆C截得的弦长;
,求直线l被圆C截得的弦长;
(3)设直线AE,BF的斜率分别为 ,
, ,证明
,证明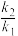 为定值,并求出该定值.
为定值,并求出该定值.
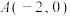 ,
,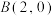 ,点P在以AB为直径的圆C上运动,
,点P在以AB为直径的圆C上运动,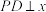 轴,垂足为D,点M满足
轴,垂足为D,点M满足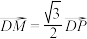 ,点M的轨迹为W,过点
,点M的轨迹为W,过点 的直线l交W于点E、F.
的直线l交W于点E、F.(1)求W的方程;
(2)若直线l的倾斜角为
 ,求直线l被圆C截得的弦长;
,求直线l被圆C截得的弦长;(3)设直线AE,BF的斜率分别为
 ,
, ,证明
,证明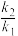 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
5 . 已知双曲线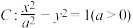 的焦距为
的焦距为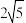 且左右顶点分别为
且左右顶点分别为 ,过点
,过点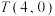 的直线
的直线 与双曲线
与双曲线 的右支交于
的右支交于 两点.
两点.
(1)求双曲线的方程;
(2)记直线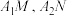 的斜率分别为
的斜率分别为 ,证明:
,证明: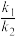 是定值;
是定值;
(3)设 为直线
为直线 和
和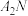 的交点,记
的交点,记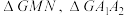 的面积分别为
的面积分别为 ,求
,求 的最小值.
的最小值.
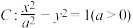 的焦距为
的焦距为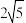 且左右顶点分别为
且左右顶点分别为 ,过点
,过点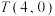 的直线
的直线 与双曲线
与双曲线 的右支交于
的右支交于 两点.
两点.(1)求双曲线的方程;
(2)记直线
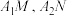 的斜率分别为
的斜率分别为 ,证明:
,证明: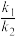 是定值;
是定值;(3)设
 为直线
为直线 和
和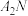 的交点,记
的交点,记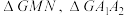 的面积分别为
的面积分别为 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024高二上·全国·专题练习
名校
6 . 已知两个非零向量 ,
, ,在空间任取一点
,在空间任取一点 ,作
,作 ,
,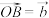 ,则
,则 叫做向量
叫做向量 ,
, 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 ,
, 都垂直,它的模
都垂直,它的模 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 为
为 上一点,
上一点,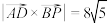 .
. 的长;
的长;
(2)若 为
为 的中点,求二面角
的中点,求二面角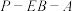 的余弦值;
的余弦值;
(3)若 为
为 上一点,且满足
上一点,且满足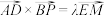 ,求
,求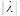 .
.
 ,
, ,在空间任取一点
,在空间任取一点 ,作
,作 ,
,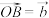 ,则
,则 叫做向量
叫做向量 ,
, 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 ,
, 都垂直,它的模
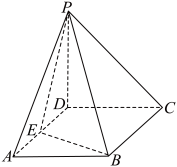
都垂直,它的模 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
, ,
, 为
为 上一点,
上一点,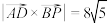 .
.
 的长;
的长;(2)若
 为
为 的中点,求二面角
的中点,求二面角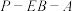 的余弦值;
的余弦值;(3)若
 为
为 上一点,且满足
上一点,且满足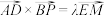 ,求
,求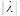 .
.
您最近一年使用:0次
2024-09-19更新
|
1294次组卷
|
8卷引用:四川省新高考教研联盟2025届高三上学期八省适应性联考模拟演练(一模)考试数学试题
四川省新高考教研联盟2025届高三上学期八省适应性联考模拟演练(一模)考试数学试题(已下线)压轴题06 空间向量与立体几何4大类型专练-【常考压轴题】(人教B版2019选择性必修第一册)新疆维吾尔自治区石河子第一中学2024-2025学年高二上学期9月月考数学试题(已下线)重组7 高二期中真题重组卷(江苏卷)A基础卷浙江省金华市磐安中学2024-2025学年高二上学期返校考试数学试题山东省青岛市第九中学2024-2025学年高二上学期第一次阶段检测数学试卷辽宁省沈阳市东北育才学校2024-2025学年高二上学期10月月考数学试卷(已下线)周测15 空间平行与垂直关系(高三一轮好卷提升卷)
7 . 已知 为曲线
为曲线 上一动点,动点
上一动点,动点 到
到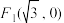 和
和 的距离之和为定值,且点
的距离之和为定值,且点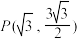 在曲线
在曲线 上.
上.
(1)求曲线 的方程;
的方程;
(2)若过点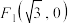 的直线
的直线 交曲线
交曲线 于
于 两点,求
两点,求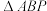 面积的取值范围.
面积的取值范围.
 为曲线
为曲线 上一动点,动点
上一动点,动点 到
到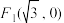 和
和 的距离之和为定值,且点
的距离之和为定值,且点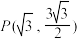 在曲线
在曲线 上.
上.(1)求曲线
 的方程;
的方程;(2)若过点
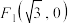 的直线
的直线 交曲线
交曲线 于
于 两点,求
两点,求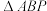 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
名校
解题方法
8 . 已知椭圆 的左、右焦点别为
的左、右焦点别为 ,
, ,离心率为
,离心率为 ,过点
,过点 的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直,
的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直, 的周长为
的周长为 ,直线
,直线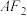 与E交于另一点C,直线
与E交于另一点C,直线 与E交于另一点D,点P为椭圆E的下顶点,如图.
与E交于另一点D,点P为椭圆E的下顶点,如图.
(2)证明:直线CD过定点.
 的左、右焦点别为
的左、右焦点别为 ,
, ,离心率为
,离心率为 ,过点
,过点 的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直,
的动直线l交E于A,B两点,点A在x轴上方,且l不与x轴垂直, 的周长为
的周长为 ,直线
,直线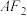 与E交于另一点C,直线
与E交于另一点C,直线 与E交于另一点D,点P为椭圆E的下顶点,如图.
与E交于另一点D,点P为椭圆E的下顶点,如图.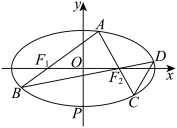
(2)证明:直线CD过定点.
您最近一年使用:0次
2024-09-03更新
|
702次组卷
|
4卷引用:四川省成都市外国语学校2023-2024学年高二下学期期末考试数学试题
四川省成都市外国语学校2023-2024学年高二下学期期末考试数学试题(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【练】(高二期中压轴专项)(已下线)专题1 特殊探路 直接求解(经典好题母题)【练】河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期10月月考数学试题
名校
解题方法
9 . 定义:若椭圆 上的两个点
上的两个点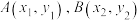 满足
满足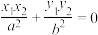 ,则称
,则称 为该椭圆的一个“共轭点对”,记作
为该椭圆的一个“共轭点对”,记作 .已知椭圆
.已知椭圆 的一个焦点坐标为
的一个焦点坐标为 ,且椭圆过点
,且椭圆过点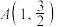 .
.
(1)求椭圆C的标准方程;
(2)求证:有两个点 满足“共轭点对”
满足“共轭点对” ,并求出
,并求出 的坐标;
的坐标;
(3)设(2)中的两个点 分别是
分别是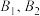 ,设
,设 为坐标原点,点
为坐标原点,点 在椭圆
在椭圆 上,且
上,且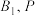 ,
,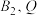 顺时针排列且
顺时针排列且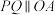 ,证明:四边形
,证明:四边形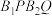 的面积小于
的面积小于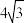 .
.
 上的两个点
上的两个点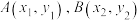 满足
满足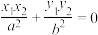 ,则称
,则称 为该椭圆的一个“共轭点对”,记作
为该椭圆的一个“共轭点对”,记作 .已知椭圆
.已知椭圆 的一个焦点坐标为
的一个焦点坐标为 ,且椭圆过点
,且椭圆过点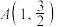 .
.(1)求椭圆C的标准方程;
(2)求证:有两个点
 满足“共轭点对”
满足“共轭点对” ,并求出
,并求出 的坐标;
的坐标;(3)设(2)中的两个点
 分别是
分别是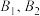 ,设
,设 为坐标原点,点
为坐标原点,点 在椭圆
在椭圆 上,且
上,且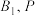 ,
,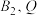 顺时针排列且
顺时针排列且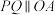 ,证明:四边形
,证明:四边形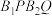 的面积小于
的面积小于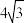 .
.
您最近一年使用:0次
2024-08-30更新
|
431次组卷
|
6卷引用:四川省达州市通川区2024-2025学年高三上学期开学摸底联考数学试题
四川省达州市通川区2024-2025学年高三上学期开学摸底联考数学试题四川省遂宁市蓬溪中学校2025届高三开学摸底联考数学试卷河南省名校联盟2025届高三上学期开学摸底联考数学试题(已下线)重难点突破07 圆锥曲线三角形面积与四边形面积题型归类(七大题型)(已下线)拔高点突破03 圆锥曲线背景下的新定义问题(八大题型)广东省广州市第六中学2024-2025学年高三上学期10月阶段训练数学试题
名校
10 . 如下图,在 中,
中,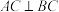 ,
,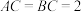 ,D是AC中点,E、F分别是BA、BC边上的动点,且
,D是AC中点,E、F分别是BA、BC边上的动点,且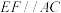 ;将
;将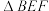 沿EF折起,将点B折至点P的位置,得到四棱锥;
沿EF折起,将点B折至点P的位置,得到四棱锥; ;
;
(2)若 ,二面角
,二面角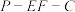 是直二面角,求二面角
是直二面角,求二面角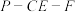 的正切值;
的正切值;
(3)当 时,求直线PE与平面ABC所成角的正弦值的取值范围.
时,求直线PE与平面ABC所成角的正弦值的取值范围.
 中,
中,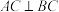 ,
,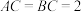 ,D是AC中点,E、F分别是BA、BC边上的动点,且
,D是AC中点,E、F分别是BA、BC边上的动点,且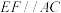 ;将
;将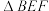 沿EF折起,将点B折至点P的位置,得到四棱锥;
沿EF折起,将点B折至点P的位置,得到四棱锥; 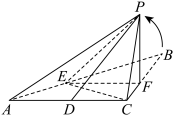
 ;
;(2)若
 ,二面角
,二面角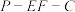 是直二面角,求二面角
是直二面角,求二面角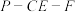 的正切值;
的正切值;(3)当
 时,求直线PE与平面ABC所成角的正弦值的取值范围.
时,求直线PE与平面ABC所成角的正弦值的取值范围.
您最近一年使用:0次
2024-08-29更新
|
2353次组卷
|
8卷引用:四川省成都市第七中学2024-2025学年高二上学期10月测试数学试题
(已下线)四川省成都市第七中学2024-2025学年高二上学期10月测试数学试题黑龙江省哈尔滨市第九中学校2024-2025学年高二上学期八月学业阶段性评价考试数学试卷广西南宁市第三中五象校区学2024-2025学年高二上学期月考数学试题(一)(已下线)微点4 空间向量的应用【练】(高中同步进阶微专题)河南省开封市龙亭区河南大学附属中学2024-2025学年高二上学期10月月考数学试题重庆市第二十九中学2024-2025学年高二上学期第1次月考数学试题河南省新乡市河南师范大学附属中学2024-2025学年高二上学期10月月考数学试卷广东省广州市第五中学2024-2025学年高二上学期第一次段考数学试卷



