名校
解题方法
1 . 在空间直角坐标系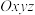 中,过点
中,过点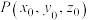 且以
且以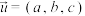 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为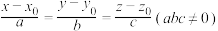 ,过点
,过点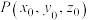 且以
且以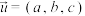 为法向量的平面方程可表示为
为法向量的平面方程可表示为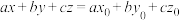 .
.
(1)若直线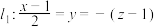 与
与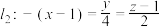 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;
(2)在三棱柱 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面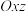 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;
(3)若集合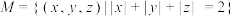 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
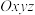 中,过点
中,过点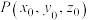 且以
且以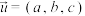 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为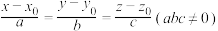 ,过点
,过点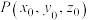 且以
且以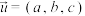 为法向量的平面方程可表示为
为法向量的平面方程可表示为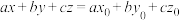 .
.(1)若直线
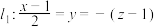 与
与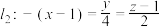 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;(2)在三棱柱
 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面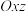 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;(3)若集合
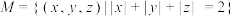 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
您最近一年使用:0次
2 . 已知集合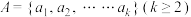 ,其中
,其中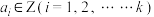 ,由
,由 中元素可构成两个点集
中元素可构成两个点集 和
和 :
: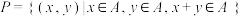 ,
, ,其中
,其中 中有
中有 个元素,
个元素, 中有
中有 个元素.新定义1个性质
个元素.新定义1个性质 :若对任意的
:若对任意的 ,必有
,必有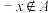 ,则称集合
,则称集合 具有性质
具有性质 .
.
(1)已知集合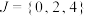 与集合
与集合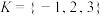 和集合
和集合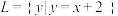 ,判断它们是否具有性质
,判断它们是否具有性质 ,若有,则直接写出其对应的集合
,若有,则直接写出其对应的集合 ,
, ;若无,请说明理由;
;若无,请说明理由;
(2)集合 具有性质
具有性质 ,若
,若 ,求:集合
,求:集合 最多有几个元素?
最多有几个元素?
(3)试判断:集合 具有性质
具有性质 是
是 的什么条件,并证明.
的什么条件,并证明.
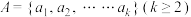 ,其中
,其中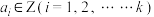 ,由
,由 中元素可构成两个点集
中元素可构成两个点集 和
和 :
: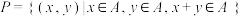 ,
, ,其中
,其中 中有
中有 个元素,
个元素, 中有
中有 个元素.新定义1个性质
个元素.新定义1个性质 :若对任意的
:若对任意的 ,必有
,必有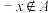 ,则称集合
,则称集合 具有性质
具有性质 .
.(1)已知集合
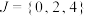 与集合
与集合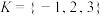 和集合
和集合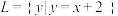 ,判断它们是否具有性质
,判断它们是否具有性质 ,若有,则直接写出其对应的集合
,若有,则直接写出其对应的集合 ,
, ;若无,请说明理由;
;若无,请说明理由;(2)集合
 具有性质
具有性质 ,若
,若 ,求:集合
,求:集合 最多有几个元素?
最多有几个元素?(3)试判断:集合
 具有性质
具有性质 是
是 的什么条件,并证明.
的什么条件,并证明.
您最近一年使用:0次
名校
解题方法
3 . 已知双曲线 的焦距为4,离心率为2,
的焦距为4,离心率为2, ,
, 分别为C的左、右焦点,两点
分别为C的左、右焦点,两点 ,
, 都在C上.
都在C上.
(1)求C的方程;
(2)若 ,求直线AB的方程;
,求直线AB的方程;
(3)若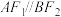 ,且
,且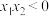 ,
,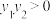 ,求四个点A,B,
,求四个点A,B, ,
, 所构成四边形的面积的最小值.
所构成四边形的面积的最小值.
 的焦距为4,离心率为2,
的焦距为4,离心率为2, ,
, 分别为C的左、右焦点,两点
分别为C的左、右焦点,两点 ,
, 都在C上.
都在C上.(1)求C的方程;
(2)若
 ,求直线AB的方程;
,求直线AB的方程;(3)若
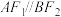 ,且
,且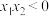 ,
,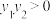 ,求四个点A,B,
,求四个点A,B, ,
, 所构成四边形的面积的最小值.
所构成四边形的面积的最小值.
您最近一年使用:0次
名校
解题方法
4 . 若一个椭圆的焦距为质数,且离心率的倒数也为质数,则称这样的椭圆为“质朴椭圆”.
(1)证明:椭圆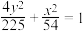 为“质朴椭圆”.
为“质朴椭圆”.
(2)是否存在实数 ,使得椭圆
,使得椭圆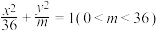 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)设斜率为 的直线
的直线 经过椭圆
经过椭圆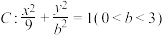 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,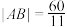 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
(1)证明:椭圆
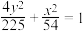 为“质朴椭圆”.
为“质朴椭圆”.(2)是否存在实数
 ,使得椭圆
,使得椭圆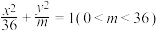 为“质朴椭圆”?若存在,求
为“质朴椭圆”?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.(3)设斜率为
 的直线
的直线 经过椭圆
经过椭圆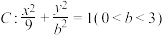 的右焦点,且与
的右焦点,且与 交于
交于 ,
, 两点,
两点,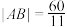 ,试问
,试问 是否为“质朴椭圆”,说明你的理由.
是否为“质朴椭圆”,说明你的理由.
您最近一年使用:0次
名校
解题方法
5 . 已知双曲线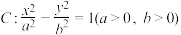 的两条渐近线方程为
的两条渐近线方程为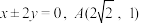 为
为 上一点.
上一点.
(1)求双曲线 的方程;
的方程;
(2)若过点 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;
(3)过双曲线 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于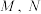 两点,记
两点,记 的中点
的中点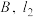 与
与 交于
交于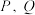 两点,记
两点,记 的中点为
的中点为 .若
.若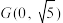 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
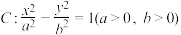 的两条渐近线方程为
的两条渐近线方程为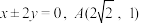 为
为 上一点.
上一点.(1)求双曲线
 的方程;
的方程;(2)若过点
 的直线
的直线 与
与 仅有1个公共点,求
仅有1个公共点,求 的方程;
的方程;(3)过双曲线
 的右焦点
的右焦点 作两条互相垂直的直线
作两条互相垂直的直线 ,
, ,且
,且 与
与 交于
交于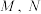 两点,记
两点,记 的中点
的中点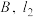 与
与 交于
交于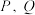 两点,记
两点,记 的中点为
的中点为 .若
.若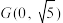 ,求点
,求点 到直线
到直线 的距离的最大值.
的距离的最大值.
您最近一年使用:0次
6 . 椭圆 与椭圆
与椭圆 :
: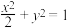 有相同的焦点,且经过点
有相同的焦点,且经过点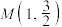 .
.
(1)求椭圆 的方程;
的方程;
(2)椭圆 的右焦点为
的右焦点为 ,设动直线
,设动直线 与坐标轴不垂直,
与坐标轴不垂直, 与椭圆
与椭圆 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 和
和 的斜率互为相反数.
的斜率互为相反数.
①证明:动直线 恒过
恒过 轴上的某个定点,并求出该定点的坐标;
轴上的某个定点,并求出该定点的坐标;
②求 面积的最大值.
面积的最大值.
 与椭圆
与椭圆 :
: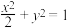 有相同的焦点,且经过点
有相同的焦点,且经过点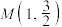 .
.(1)求椭圆
 的方程;
的方程;(2)椭圆
 的右焦点为
的右焦点为 ,设动直线
,设动直线 与坐标轴不垂直,
与坐标轴不垂直, 与椭圆
与椭圆 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 和
和 的斜率互为相反数.
的斜率互为相反数.①证明:动直线
 恒过
恒过 轴上的某个定点,并求出该定点的坐标;
轴上的某个定点,并求出该定点的坐标;②求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
7日内更新
|
1410次组卷
|
2卷引用:湖南省株洲市第二中学2024-2025学年高二上学期第一次月考(10月)数学试题
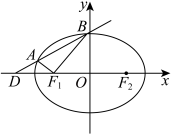
7 . 如图,已知点 、
、 分别是椭圆
分别是椭圆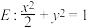 的左、右焦点,点
的左、右焦点,点 是负半轴上的一点,
是负半轴上的一点,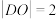 ,过点
,过点 的直线
的直线 与
与 交于点
交于点 与点
与点 .
. 面积的最大值;
面积的最大值;
(2)设直线 的斜率为
的斜率为 和直线
和直线 的斜率为
的斜率为 ,椭圆
,椭圆 上是否存在点
上是否存在点 ,使得
,使得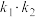 为定值,若存在,求出点
为定值,若存在,求出点 与
与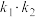 值,若不存在,请说明理由.
值,若不存在,请说明理由.
 、
、 分别是椭圆
分别是椭圆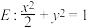 的左、右焦点,点
的左、右焦点,点 是负半轴上的一点,
是负半轴上的一点,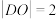 ,过点
,过点 的直线
的直线 与
与 交于点
交于点 与点
与点 .
.
 面积的最大值;
面积的最大值;(2)设直线
 的斜率为
的斜率为 和直线
和直线 的斜率为
的斜率为 ,椭圆
,椭圆 上是否存在点
上是否存在点 ,使得
,使得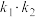 为定值,若存在,求出点
为定值,若存在,求出点 与
与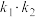 值,若不存在,请说明理由.
值,若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
8 . 已知两个非零向量 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
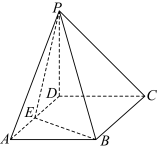
都垂直,它的模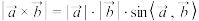 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,
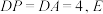 为线段
为线段 上一点,
上一点,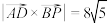 .
. 的长;
的长;
(2)若 为
为 的中点,求二面角
的中点,求二面角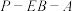 的正弦值;
的正弦值;
(3)若 为线段
为线段 上一点,且满足
上一点,且满足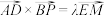 ,求
,求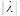 .
.
 ,在空间任取一点
,在空间任取一点 ,作
,作 ,则
,则 叫做向量
叫做向量 的夹角,记作
的夹角,记作 .定义
.定义 与
与 的“向量积”为:
的“向量积”为: 是一个向量,它与向量
是一个向量,它与向量 都垂直,它的模
都垂直,它的模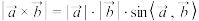 .如图,在四棱锥
.如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 底面
底面 ,
,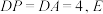 为线段
为线段 上一点,
上一点,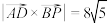 .
.
 的长;
的长;(2)若
 为
为 的中点,求二面角
的中点,求二面角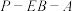 的正弦值;
的正弦值;(3)若
 为线段
为线段 上一点,且满足
上一点,且满足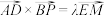 ,求
,求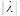 .
.
您最近一年使用:0次
7日内更新
|
474次组卷
|
3卷引用:吉林省长春吉大附中实验学校2024-2025学年高二上学期第一次月考数学试题
名校
9 . 已知椭圆 的离心率为
的离心率为 ,左顶点
,左顶点 与上顶点
与上顶点 的距离为
的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)点 在椭圆
在椭圆 上,且
上,且 点不在
点不在 轴上,线段
轴上,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点 ,若
,若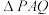 为等边三角形,求直线
为等边三角形,求直线 的方程.
的方程.
 的离心率为
的离心率为 ,左顶点
,左顶点 与上顶点
与上顶点 的距离为
的距离为 .
.(1)求椭圆
 的方程;
的方程;(2)点
 在椭圆
在椭圆 上,且
上,且 点不在
点不在 轴上,线段
轴上,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点 ,若
,若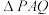 为等边三角形,求直线
为等边三角形,求直线 的方程.
的方程.
您最近一年使用:0次
名校
10 . “曼哈顿距离”是十九世纪的赫尔曼 闵可夫斯基所创词汇,它是一种使用几何度量空间的几何用语,定义如下:在平面直角坐标中的任意两点
闵可夫斯基所创词汇,它是一种使用几何度量空间的几何用语,定义如下:在平面直角坐标中的任意两点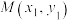 ,
,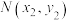 的曼哈顿距离为
的曼哈顿距离为 .已知在四边形
.已知在四边形 中,
中,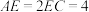 ,
, ,
,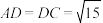 ,且
,且 平分
平分 ,若将
,若将 沿线段
沿线段 向上折叠,使二面角
向上折叠,使二面角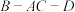 为直二面角,如图所示,折叠后点
为直二面角,如图所示,折叠后点 在新图形中对应点记为
在新图形中对应点记为 .
.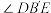 的大小;
的大小;
(2)若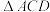 所在平面为
所在平面为 ,设
,设 ,且
,且 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(i)判断 是什么曲线,并求出对应的方程;
是什么曲线,并求出对应的方程;
(ii)设 为平面
为平面 上过点
上过点 且与直线
且与直线 垂直的直线,已知
垂直的直线,已知 在直线
在直线 上,
上, 在
在 上,求
上,求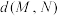 的最小值.
的最小值.
 闵可夫斯基所创词汇,它是一种使用几何度量空间的几何用语,定义如下:在平面直角坐标中的任意两点
闵可夫斯基所创词汇,它是一种使用几何度量空间的几何用语,定义如下:在平面直角坐标中的任意两点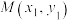 ,
,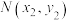 的曼哈顿距离为
的曼哈顿距离为 .已知在四边形
.已知在四边形 中,
中,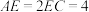 ,
, ,
,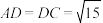 ,且
,且 平分
平分 ,若将
,若将 沿线段
沿线段 向上折叠,使二面角
向上折叠,使二面角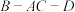 为直二面角,如图所示,折叠后点
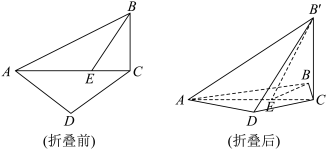
为直二面角,如图所示,折叠后点 在新图形中对应点记为
在新图形中对应点记为 .
.
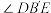 的大小;
的大小;(2)若
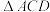 所在平面为
所在平面为 ,设
,设 ,且
,且 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(i)判断
 是什么曲线,并求出对应的方程;
是什么曲线,并求出对应的方程;(ii)设
 为平面
为平面 上过点
上过点 且与直线
且与直线 垂直的直线,已知
垂直的直线,已知 在直线
在直线 上,
上, 在
在 上,求
上,求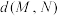 的最小值.
的最小值.
您最近一年使用:0次



