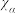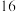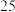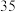1 . (1)化简求值: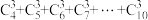 ;
;
(2)解方程: ;
;
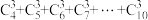 ;
;(2)解方程:
 ;
;
您最近半年使用:0次
2022-03-29更新
|
823次组卷
|
3卷引用:福建省三明第一中学2021-2022学年高二下学期第一次月考数学试题
福建省三明第一中学2021-2022学年高二下学期第一次月考数学试题江苏省淮安市楚州中学、新马中学2022-2023学年高二下学期期中联考数学试题(已下线)6.2.3组合-6.2.4组合数——课堂例题
名校
解题方法
2 . 学生考试中答对但得不了满分的原因多为答题不规范,具体表现为:解题结果正确,无明显推理错误,但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等,记此类解答为“B类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“B类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于或等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.假设本次考试阅卷老师对满分为12分的题目中的“B类解答”所评分数及比例均如上表的所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“B类解答”,求甲同学此题需要仲裁的概率.
(2)本次数学考试中甲同学某题(满分12分)的解答属于“B类解答”,求甲同学此题得分 的分布列及数学期望
的分布列及数学期望 ;
;
(3)本次数学考试有6个解答题,每题满分均为12分,同学乙6个题的解答均为“B类解答”,记该同学6个题中得分为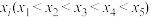 的题目个数为
的题目个数为 ,
, (N为自然数)
(N为自然数)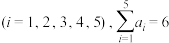 ,计算事件
,计算事件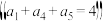 的概率.
的概率.
教师评分 | 11 | 10 | 9 |
各分数所占比例 | 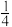 |  | 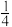 |
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于或等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.假设本次考试阅卷老师对满分为12分的题目中的“B类解答”所评分数及比例均如上表的所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“B类解答”,求甲同学此题需要仲裁的概率.
(2)本次数学考试中甲同学某题(满分12分)的解答属于“B类解答”,求甲同学此题得分
 的分布列及数学期望
的分布列及数学期望 ;
;(3)本次数学考试有6个解答题,每题满分均为12分,同学乙6个题的解答均为“B类解答”,记该同学6个题中得分为
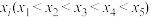 的题目个数为
的题目个数为 ,
, (N为自然数)
(N为自然数)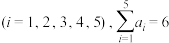 ,计算事件
,计算事件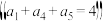 的概率.
的概率.
您最近半年使用:0次
2020-08-06更新
|
236次组卷
|
7卷引用:福建省安溪一中、养正中学、惠安一中、泉州实验中学2019-2020学年高二下学期期末联考数学试题
福建省安溪一中、养正中学、惠安一中、泉州实验中学2019-2020学年高二下学期期末联考数学试题山东省九校2019-2020学年高三上学期12月检测数学试题(已下线)卷05-备战2020年新高考数学自学检测黄金10卷-《2020年新高考政策解读与配套资源》山西省太原市第五中学2020届高三下学期3月摸底数学(理)试题(已下线)考点33 离散型随机变量的概率-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题22 离散型随机变量的概率-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】(已下线)专题9.2 离散型随机变量的均值与方差-备战2021年高考数学精选考点专项突破题集(新高考地区)
名校
解题方法
3 . 某大学为了解学生对学校食堂服务的满意度,随机调查了 名男生和
名男生和 名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如下所示的列联表,经计算
名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如下所示的列联表,经计算 ,则可以推断出( )
,则可以推断出( )
表1
表2
 名男生和
名男生和 名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如下所示的列联表,经计算
名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如下所示的列联表,经计算 ,则可以推断出( )
,则可以推断出( )表1
满意 | 不满意 | |
男 |
|
|
女 |
|
|
|
|
|
|
|
|
|
|
A.该学校男生对食堂服务满意的概率的估计值为 |
| B.调研结果显示,该学校男生比女生对食堂服务更满意 |
C.认为男、女生对该食堂服务的评价有差异此推断犯错误的概率不超过 |
D.认为男、女生对该食堂服务的评价有差异此推断犯错误的概率不超过 |
您最近半年使用:0次
解题方法
4 . 一道试题,甲解出的概率为 ,乙解出的概率为
,乙解出的概率为 .设解出该题的人数为X,则D(X)等于( )
.设解出该题的人数为X,则D(X)等于( )
 ,乙解出的概率为
,乙解出的概率为 .设解出该题的人数为X,则D(X)等于( )
.设解出该题的人数为X,则D(X)等于( )A. | B.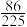 |
C. | D.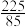 |
您最近半年使用:0次
2021-05-07更新
|
983次组卷
|
4卷引用:福建省莆田市第二十四中学2020-2021学年高二下学期第二次月考数学试题(B卷)
福建省莆田市第二十四中学2020-2021学年高二下学期第二次月考数学试题(B卷)(已下线)7.3.2 离散型随机变量的方差(练习)-2020-2021学年下学期高二数学同步精品课堂(新教材人教A版选择性必修第三册)(已下线)【新教材精创】7.3.2离散型随机变量的方差 -B提高练2023版 北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差
名校
5 . 某高中学校为了解学生参加体育锻炼的情况,统计了全校所有学生在一年内每周参加体育锻炼的次数,现随机抽取了60名同学在某一周参加体育锻炼的数据,结果如下表:
(1)若将一周参加体育锻炼次数为3次及3次以上的,称为“经常锻炼”,其余的称为“不经常锻炼”.请完成以下 列联表,并依据小概率值
列联表,并依据小概率值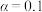 的独立性检验,能否认为性别因素与学生体育锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生体育锻炼的经常性有关系;
(2)若将一周参加体育锻炼次数为0次的称为“极度缺乏锻炼”,“极度缺乏锻炼”会导致肥胖等诸多健康问题.以样本频率估计概率,在全校抽取20名同学,其中“极度缺乏锻炼”的人数为 ,求
,求 和
和 ;
;
(3)若将一周参加体育锻炼6次或7次的同学称为“运动爱好者”,为进一步了解他们的生活习惯,在样本的10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附:
| 一周参加体育锻炼次数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 合计 |
| 男生人数 | 1 | 2 | 4 | 5 | 6 | 5 | 4 | 3 | 30 |
| 女生人数 | 4 | 5 | 5 | 6 | 4 | 3 | 2 | 1 | 30 |
| 合计 | 5 | 7 | 9 | 11 | 10 | 8 | 6 | 4 | 60 |
 列联表,并依据小概率值
列联表,并依据小概率值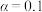 的独立性检验,能否认为性别因素与学生体育锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生体育锻炼的经常性有关系;| 性别 | 锻炼 | 合计 | |
| 不经常 | 经常 | ||
| 男生 | |||
| 女生 | |||
| 合计 | |||
 ,求
,求 和
和 ;
;(3)若将一周参加体育锻炼6次或7次的同学称为“运动爱好者”,为进一步了解他们的生活习惯,在样本的10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:

 | 0.1 | 0.05 | 0.01 |
 | 2.706 | 3.841 | 6.635 |
您最近半年使用:0次
2024-03-13更新
|
2307次组卷
|
10卷引用:福建省福州外国语学校2023-2024学年高二下学期4月期中考试数学试题
福建省福州外国语学校2023-2024学年高二下学期4月期中考试数学试题广东省广州市华南师范大学附属中学2023-2024学年高二下学期阶段检测(一)数学试题(已下线)专题8.6 成对数据的统计分析全章八大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章:成对数据的统计分析(单元测试,新题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)模块一 专题1 《线性回归与相关性和独立性检验》(北师大版高二期中)湖北省七市州2024届高三下学期3月联合统一调研测试数学试题山东省菏泽市第一中学人民路校区2024届高三下学期2月月考数学试题(已下线)【一题多变】 分类变量 独立检验山东省潍坊市昌乐北大公学学校2024届高三下学期3月监测数学试题(已下线)湖北省七市州2024届高三下学期3月联合统一调研测试数学试题变式题16-19
名校
6 . 第二十二届卡塔尔世界杯足球赛(FIFAWorldCupQatar2022)决赛中,阿根廷队通过扣人心弦的点球大战战胜了法国队.某校为了丰富学生课余生活,组建了足球社团.足球社团为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
(1)根据所给数据完成上表,并判断是否有 的把握认为该校学生喜欢足球与性别有关?
的把握认为该校学生喜欢足球与性别有关?
(2)社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知男生进球的概率为 ,女生进球的概率为
,女生进球的概率为 ,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
附: .
.
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 40 | ||
| 女生 | 30 | ||
| 合计 |
 的把握认为该校学生喜欢足球与性别有关?
的把握认为该校学生喜欢足球与性别有关?(2)社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知男生进球的概率为
 ,女生进球的概率为
,女生进球的概率为 ,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.附:
 .
. | 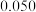 |  |  |
 |  |  |  |
您最近半年使用:0次
2023-09-12更新
|
1086次组卷
|
23卷引用:福建省厦门市五显中学2022-2023学年高二下学期期中考试数学试题
福建省厦门市五显中学2022-2023学年高二下学期期中考试数学试题(已下线)第8章 成对数据的统计分析(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020选择性必修第二册)浙江省宁波市效实中学2022-2023学年高二下学期期中数学试题海南省海南中学白沙学校2022-2023学年高二下学期期末考试数学试题河北省高碑店市崇德实验中学2022-2023学年高二下学期期中数学试题湘桂黔名校2022-2023学年高二下学期大联考数学试题福建省龙岩市上杭县第一中学2024届高三上学期12月月考数学试题江西省丰城中学2023-2024学年高二下学期3月月考数学试题江苏省南通市2023届高三下学期第一次调研测试数学试题江苏省泰州市2023届高三下学期第一次调研测试数学试题重庆市万州第二高级中学2023届高三下学期第一次质量检测数学试题(已下线)模块十 计数原理与统计概率-1重庆市长寿中学2022-2023学年高三下学期3月月考数学试题安徽省蚌埠市2023届高三第三次教学质量检查考试数学试题河北省高碑店市崇德实验中学2023届高三下学期期中数学试题广东省揭阳市普宁国贤学校2024届高三上学期开学考试数学试题(已下线)专题09 计数原理与概率统计-3宁夏回族自治区石嘴山市平罗县平罗中学2023届高三二模理科数学试题四川省宜宾市叙州区第一中学校2023届高三三诊模拟考试数学(理)试题(已下线)考点巩固卷23 统计与统计案例(十大考点)广东省湛江市爱周中学2024届高三上学期调研考前模拟 (一)数学试题(已下线)广东省佛山市南海区桂城中学2024届高三上学期11月月考数学试题四川省成都市金苹果锦城第一中学2024届高三上学期期中数学(理)试题
名校
解题方法
7 . 某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下,得分在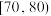 内的学生获三等奖,得分在
内的学生获三等奖,得分在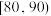 内的学生获二等奖,得分在
内的学生获二等奖,得分在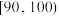 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
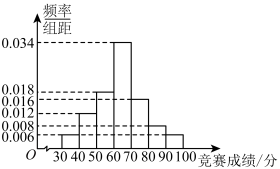
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该市所有参赛学生的成绩X近似服从正态分布 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:
①若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
②若从所有参赛学生中(参赛学生数大于10000)随机抽取4名学生进行访谈,求其中竞赛成绩在64分以上的学生人数的期望与方差.
附参考数据:若随机变量X服从正态分布 ,则
,则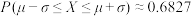 ,
,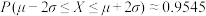 ,
,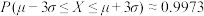 .
.
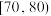 内的学生获三等奖,得分在
内的学生获三等奖,得分在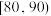 内的学生获二等奖,得分在
内的学生获二等奖,得分在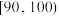 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该市所有参赛学生的成绩X近似服从正态分布
 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:①若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
②若从所有参赛学生中(参赛学生数大于10000)随机抽取4名学生进行访谈,求其中竞赛成绩在64分以上的学生人数的期望与方差.
附参考数据:若随机变量X服从正态分布
 ,则
,则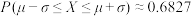 ,
,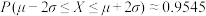 ,
,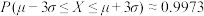 .
.
您最近半年使用:0次
2023-04-13更新
|
983次组卷
|
2卷引用:福建省福州第三中学2022-2023学年高二下学期期中适应性练习数学试题
解题方法
8 . 开展中小学生课后服务,是促进学生健康成长、帮助家长解决接送学生困难的重要举措,是进一步增强教育服务能力、使人民群众具有更多获得感和幸福感的民生工程,某校为确保学生课后服务工作顺利开展,制定了两套工作方案,为了解学生对这两个方案的支持情况,现随机抽取 个学生进行调查,获得数据如下表:假设用频率估计概率,且所有学生对活动方案是否支持相互独立,
个学生进行调查,获得数据如下表:假设用频率估计概率,且所有学生对活动方案是否支持相互独立,
(1)从该校支持方案一和支持方案二的学生中各随机抽取 人,设
人,设 为抽出两人中女生的个数,求
为抽出两人中女生的个数,求 的分布列;
的分布列;
(2)在(1)中, 表示抽出两人中男生的个数,试判断方差
表示抽出两人中男生的个数,试判断方差 与
与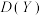 的大小,(直接写结果)
的大小,(直接写结果)
 个学生进行调查,获得数据如下表:假设用频率估计概率,且所有学生对活动方案是否支持相互独立,
个学生进行调查,获得数据如下表:假设用频率估计概率,且所有学生对活动方案是否支持相互独立,男 | 女 | |
支持方案一 |
|
|
支持方案二 |
|
|
 人,设
人,设 为抽出两人中女生的个数,求
为抽出两人中女生的个数,求 的分布列;
的分布列;(2)在(1)中,
 表示抽出两人中男生的个数,试判断方差
表示抽出两人中男生的个数,试判断方差 与
与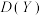 的大小,(直接写结果)
的大小,(直接写结果)
您最近半年使用:0次
解题方法
9 . 为普及传染病防治知识,增强学生的疾病防范意识,提高自身保护能力,校委会在全校学生范围内,组织了一次传染病及个人卫生相关知识有奖竞赛(满分100分),竞赛奖励规则如下:得分在 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
(1)从该样本中随机抽取2名学生的竞赛成绩,求这2名学生恰有一名学生获奖的概率;
(2)若该校所有参赛学生的成绩X近似地服从正态分布 ,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为
,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.
内的学生获一等奖,其它学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如图所示的频率分布表.| 竞赛成绩 | 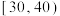 | 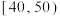 |  |  |  |  |  |
| 人数 | 6 | 12 | 18 | 34 | 16 | 8 | 6 |
(2)若该校所有参赛学生的成绩X近似地服从正态分布
 ,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为
,若从所有参赛学生中(参赛学生人数大于10000)随机抽取4名学生进行座谈,设其中竞赛成绩在64分以上的学生人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
10 . 为了解学校学生的睡眠情况,决定抽取20名学生对其睡眠时间进行调查,统计如下:
(1)记“足8小时”为睡眠充足,“不足8小时”为睡眠不充足,完成下面的列联表,并判断是否有90%的把握认为“睡眠充足与否”与性别有关;
(2)现从抽出的11位女生中再随机抽取3人,记X为睡眠时间“不足8小时足7小时”的女生人数,求X的分布列和均值.
附: ;
;
性别/睡眠时间 | 足8小时 | 不足8小时足7小时 | 不足7小时 |
男生 | 3 | 5 | 1 |
女生 | 1 | 7 | 3 |
睡眠情况 | 性别 | 合计 | |
男生 | 女生 | ||
睡眠充足 | |||
睡眠不充足 | |||
合计 | |||
附:
 ;
;
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
2022-06-23更新
|
442次组卷
|
2卷引用:福建省泉州科技中学2021-2022学年高二下学期期末数学试题