1 . 已知椭圆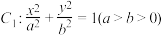 的离心率为
的离心率为 ,椭圆
,椭圆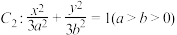 经过点
经过点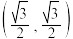 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)设点 是椭圆
是椭圆 上的任意一点,射线
上的任意一点,射线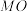 与椭圆
与椭圆 交于点
交于点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 有且只有一个公共点,直线
有且只有一个公共点,直线 与椭圆
与椭圆 交于
交于 两个相异点,证明:
两个相异点,证明: 面积为定值.
面积为定值.
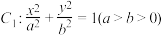 的离心率为
的离心率为 ,椭圆
,椭圆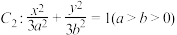 经过点
经过点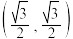 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)设点
 是椭圆
是椭圆 上的任意一点,射线
上的任意一点,射线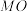 与椭圆
与椭圆 交于点
交于点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 有且只有一个公共点,直线
有且只有一个公共点,直线 与椭圆
与椭圆 交于
交于 两个相异点,证明:
两个相异点,证明: 面积为定值.
面积为定值.
您最近一年使用:0次
2020-12-07更新
|
360次组卷
|
15卷引用:【校级联考】河北省示范性高中2019届高三下学期4月联考数学(文)试题
【校级联考】河北省示范性高中2019届高三下学期4月联考数学(文)试题【省级联考】河北省示范性高中2019届高三4月联考数学(理)试题【市级联考】山西省晋城市2019届高三第二次模拟考试数学(文)(B卷)试题【市级联考】山西省晋城市2019届高三第二次模拟考试数学(理科)试题山西省名师联盟2019届高三5月内部特供卷理科数学 试题【校级联考】山西名师联盟2019届高三5月内部特供卷文科数学试题四川省成都市双流区棠湖中学2019-2020学年高三上学期期中数学试题广东省六校联盟2019-2020学年高三上学期第一次联考数学(文)试题(已下线)专题06 解析几何中的定点、定值问题(第五篇)-备战2020年高考数学大题精做之解答题题型全覆盖(已下线)专题07 解析几何中的证明问题(第五篇)-备战2020年高考数学大题精做之解答题题型全覆盖(已下线)专题9.7 圆锥曲线综合问题(练)-2021年新高考数学一轮复习讲练测(已下线)专题9.7 圆锥曲线综合问题(精练)-2021年新高考数学一轮复习学与练安徽省合肥市第十中学2020-2021学年高三上学期12月阶段性检测数学(理)试题重庆市青木关中学2021-2022学年高二上学期第三次月考数学试题安徽省滁州市定远县育才学校2021-2022学年高三下学期适应性考试(最后一卷)数学(理)试题
2 . 如图,已知三棱锥A-BPC中,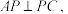
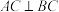 ,M为AB的中点,D为PB的中点,且
,M为AB的中点,D为PB的中点,且 为正三角形.
为正三角形.
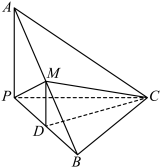
(1)求证: 平面APC;
平面APC;
(2)若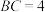 ,
, ,求三棱锥D-BCM的体积.
,求三棱锥D-BCM的体积.
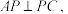
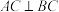 ,M为AB的中点,D为PB的中点,且
,M为AB的中点,D为PB的中点,且 为正三角形.
为正三角形.
(1)求证:
 平面APC;
平面APC;(2)若
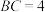 ,
, ,求三棱锥D-BCM的体积.
,求三棱锥D-BCM的体积.
您最近一年使用:0次
名校
3 . 已知函数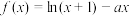 ,其中
,其中 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)当 的图像刚好与
的图像刚好与 轴相切时,设函数
轴相切时,设函数 ,其中
,其中 ,求证:
,求证: 存在极小值且该极小值小于
存在极小值且该极小值小于 .
.
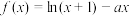 ,其中
,其中 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)当
 的图像刚好与
的图像刚好与 轴相切时,设函数
轴相切时,设函数 ,其中
,其中 ,求证:
,求证: 存在极小值且该极小值小于
存在极小值且该极小值小于 .
.
您最近一年使用:0次
2019-10-12更新
|
383次组卷
|
2卷引用:重庆市第一中学2018-2019学年高二下学期期末数学(理)试题
名校
4 . 已知函数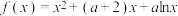 .
.
(1)讨论函数 的单调区间;
的单调区间;
(2)若存在两个不相等的正数 ,
, ,满足
,满足 ,证明:
,证明: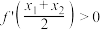 .
.
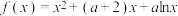 .
.(1)讨论函数
 的单调区间;
的单调区间;(2)若存在两个不相等的正数
 ,
, ,满足
,满足 ,证明:
,证明: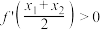 .
.
您最近一年使用:0次
名校
5 . 已知椭圆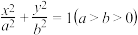 右焦点
右焦点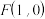 ,离心率为
,离心率为 ,过
,过 作两条互相垂直的弦
作两条互相垂直的弦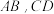 ,设
,设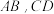 中点分别为
中点分别为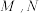 .
.
(1)求椭圆的标准方程;
(2)证明:直线 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.
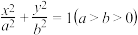 右焦点
右焦点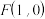 ,离心率为
,离心率为 ,过
,过 作两条互相垂直的弦
作两条互相垂直的弦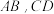 ,设
,设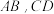 中点分别为
中点分别为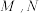 .
.(1)求椭圆的标准方程;
(2)证明:直线
 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.
您最近一年使用:0次
2018-11-29更新
|
535次组卷
|
4卷引用:【全国百强校】重庆市西南大学附属中学校2019届高三上学期第三次月考数学(理)试题
名校
6 . 已知函数 .
.
 求
求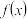 的单调区间;
的单调区间;
 Ⅱ
Ⅱ 证明:
证明: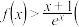 其中e是自然对数的底数,
其中e是自然对数的底数,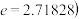 .
.
 .
. 求
求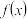 的单调区间;
的单调区间; Ⅱ
Ⅱ 证明:
证明: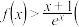 其中e是自然对数的底数,
其中e是自然对数的底数,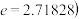 .
.
您最近一年使用:0次
2018-12-10更新
|
508次组卷
|
2卷引用:【全国百强校】重庆市重庆第一中学2019届高三(上)期中数学试卷(文科)
7 . 定义域为 的函数
的函数 满足:
满足: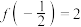 ,且对于任意实数
,且对于任意实数 ,
, 恒有
恒有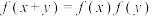 ,当
,当 时,
时,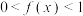 .
.
(1)求 的值,并证明当
的值,并证明当 时,
时, ;
;
(2)判断函数 在
在 上的单调性并加以证明;
上的单调性并加以证明;
(3)若不等式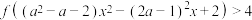 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的函数
的函数 满足:
满足: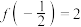 ,且对于任意实数
,且对于任意实数 ,
, 恒有
恒有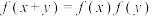 ,当
,当 时,
时,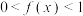 .
.(1)求
 的值,并证明当
的值,并证明当 时,
时, ;
;(2)判断函数
 在
在 上的单调性并加以证明;
上的单调性并加以证明;(3)若不等式
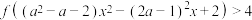 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-06-06更新
|
1573次组卷
|
5卷引用:重庆市蜀都中学2020-2021学年高一上学期12月月考数学试题
重庆市蜀都中学2020-2021学年高一上学期12月月考数学试题【全国百强校】河北省深州市中学2017-2018高一下学期期末考试数学试题(已下线)2019年7月21日 《每日一题》2020届高考一轮复习(理科)—— 每周一测(已下线)2019年7月21日 《每日一题》2020届高考一轮复习(文科)—— 每周一测湖北省部分重点中学2019-2020学年高一上学期第一次联考数学试题
8 . 设椭圆 过点
过点  ,且左焦点为
,且左焦点为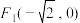
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当过点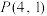 的动直线
的动直线  与椭圆
与椭圆 相交与两不同点
相交与两不同点  时,在线段
时,在线段 上取点
上取点  ,满足
,满足 ,证明:点
,证明:点  总在某定直线上
总在某定直线上
 过点
过点  ,且左焦点为
,且左焦点为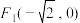
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当过点
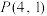 的动直线
的动直线  与椭圆
与椭圆 相交与两不同点
相交与两不同点  时,在线段
时,在线段 上取点
上取点  ,满足
,满足 ,证明:点
,证明:点  总在某定直线上
总在某定直线上
您最近一年使用:0次
2016-11-30更新
|
7629次组卷
|
14卷引用:2014届重庆市第八中学高三第四次月考理科数学试卷
(已下线)2014届重庆市第八中学高三第四次月考理科数学试卷2008年普通高等学校招生全国统一考试理科数学(安徽卷)【全国百强校】四川省南充市阆中中学2018-2019学年高二3月月考理科数学试题【全国百强校】四川省南充市阆中中学2018-2019学年高二3月月考文科数学试题沪教版(上海) 高三年级 新高考辅导与训练 第十一章 圆锥曲线 三、参数方程2008 年普通高等学校招生考试数学(理)试题(安徽卷)(已下线)专题12 解析几何中的定值、定点和定线问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题7 圆锥曲线之极点与极线 微点1 圆锥曲线之极点与极线(已下线)专题7 圆锥曲线之极点与极线 微点2 极点与极线问题常见模型总结(已下线)专题41 定比点差法、齐次化、极点极线问题、蝴蝶问题(已下线)第五篇 向量与几何 专题5 调和点列 微点2 调和点列(二)(已下线)第五篇 向量与几何 专题6 调和线束 微点1 调和线束(一)(已下线)专题18 圆锥曲线高频压轴解答题(16大核心考点)(讲义)-2(已下线)大招16极点极线
名校
9 . 已知函数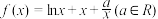 .
.
(1)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围;
的取值范围;
(2)若函数 有两个不同的极值点,记作
有两个不同的极值点,记作 ,
, ,且
,且 ,证明:
,证明: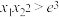 (
( 为自然对数).
为自然对数).
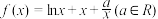 .
.(1)若函数
 在
在 上为增函数,求
上为增函数,求 的取值范围;
的取值范围;(2)若函数
 有两个不同的极值点,记作
有两个不同的极值点,记作 ,
, ,且
,且 ,证明:
,证明: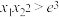 (
( 为自然对数).
为自然对数).
您最近一年使用:0次
2018-07-18更新
|
3258次组卷
|
15卷引用:【全国百强校】山东省栖霞二中2017-2018学年高二下学期期末考试理数试题
【全国百强校】山东省栖霞二中2017-2018学年高二下学期期末考试理数试题(已下线)【全国百强校】河北省衡水中学2019届高三上学期二调考试数学(文)试题【全国百强校】江西省南昌市第十中学2019届高三上学期期中考试数学(文)试题【全国百强校】江西省南昌市第十中学2019届高三上学期期中考试数学(理)试题湖南省长沙市长郡中学2019-2020学年高三10月月考数学(理)试题湖北省黄冈市浠水县实验高级中学2019-2020学年高三上学期8月月考数学(文)试题2020届江西省赣州市十五县市高三上学期期中联考数学理科试题2019届四川省仁寿第一中学校南校区高三第五次模拟考试数学(文)试题(已下线)专题05 用好导数,破解函数零点问题(第一篇)-2020高考数学压轴题命题区间探究与突破湖南省长沙市长郡中学2019-2020学年高三上学期第二次月考理科数学试题(已下线)专题05 函数与不等式相结合(第六篇)-备战2020年高考数学大题精做之解答题题型全覆盖江西赣州市十五县(市)2021届高三上学期期中联考数学(理)试题甘肃省天水市甘谷县2020-2021学年高三上学期第四次检测数学(理)试题重庆市第三十七中学校2020-2021学年高二下学期5月月考数学试题福建省龙岩第一中学2021届高三上学期第三次月考数学试题



