解题方法
1 . 对于数列 ,设
,设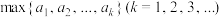 表示数列
表示数列 前
前 项
项 ,
, ,
, ,
,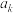 中的最大项.数列
中的最大项.数列 满足:
满足: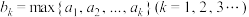 .
.
(1)若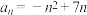 ,求
,求 的前
的前 项和.
项和.
(2)设数列 为等差数列,证明:
为等差数列,证明: 或者
或者 (
( 为常数),
为常数), ,
, ,
, ,
, .
.
(3)设数列 为等差数列,公差为
为等差数列,公差为 ,且
,且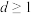 .
.
记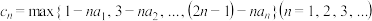 ,
,
求证:数列 是等差数列.
是等差数列.
 ,设
,设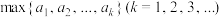 表示数列
表示数列 前
前 项
项 ,
, ,
, ,
,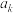 中的最大项.数列
中的最大项.数列 满足:
满足: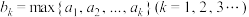 .
.(1)若
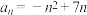 ,求
,求 的前
的前 项和.
项和.(2)设数列
 为等差数列,证明:
为等差数列,证明: 或者
或者 (
( 为常数),
为常数), ,
, ,
, ,
, .
.(3)设数列
 为等差数列,公差为
为等差数列,公差为 ,且
,且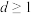 .
.记
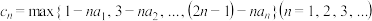 ,
,求证:数列
 是等差数列.
是等差数列.
您最近一年使用:0次
名校
解题方法
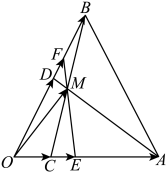
2 . 如图所示,在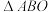 中,
中,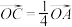 ,
,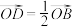 ,
, 与
与 相交于点
相交于点 ,设
,设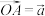 ,
,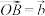 .
.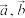 表示
表示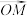 ;
;
(2)过点 作直线
作直线 分别交线段
分别交线段 于点
于点 ,记
,记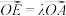 ,
,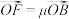 ,求证:不论点
,求证:不论点 在线段
在线段 上如何移动,
上如何移动,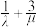 为定值.
为定值.
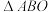 中,
中,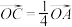 ,
,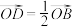 ,
, 与
与 相交于点
相交于点 ,设
,设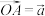 ,
,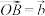 .
.
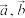 表示
表示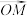 ;
;(2)过点
 作直线
作直线 分别交线段
分别交线段 于点
于点 ,记
,记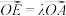 ,
,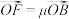 ,求证:不论点
,求证:不论点 在线段
在线段 上如何移动,
上如何移动,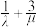 为定值.
为定值.
您最近一年使用:0次
2023-02-02更新
|
4704次组卷
|
25卷引用:【全国百强校】广西宾阳县宾阳中学2017-2018学年高一5月月考数学试题
【全国百强校】广西宾阳县宾阳中学2017-2018学年高一5月月考数学试题四川省内江市威远中学2019-2020学年高一下学期第一次月考数学(理)试题陕西省宝鸡中学2019-2020学年高一下学期期中数学试题(A卷)巩固练08 平面向量的线性运算-2020年【衔接教材·暑假作业】新高二数学(人教版)(已下线)专题6.2 平面向量的基本定理及坐标表示(精练)-2021年新高考数学一轮复习学与练(已下线)专题6.2 平面向量的基本定理及坐标表示(练)-2021年新高考数学一轮复习讲练测(已下线)专题6.2向量基本定理与向量的坐标(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教B版)北京市第一七一中学2023-2024学年高一下学期3月调研数学试题(已下线)6.1 平面向量及其线性运算-2020-2021高中数学新教材配套提升训练(人教A版必修第二册)河北省衡水市武强中学2020-2021学年高一下学期第一次月考数学试题广西桂林市第十一中学2021-2022学年高一下学期期末阶段性质量数学试题山东省潍坊市高密市第三中学2022-2023学年高一下学期3月月考数学试题山东省烟台市招远市招远第一中学2022-2023学年高一下学期期中数学试题(已下线)专题训练:用已知向量进行线性表示-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)(已下线)期末复习01 平面向量的线性运算-期末专项复习山东省烟台市招远市第二中学2022-2023学年高一下学期3月月考数学试题江西省宁冈中学2022-2023学年高二上学期期末数学试题(已下线)核心考点01平面向量及其应用(3)广东省东莞市厚街中学2022-2023学年高一下学期3月月考数学试题专题02平面向量基本定理与平面向量的坐标表示(已下线)9.3 向量基本定理及坐标表示2-【帮课堂】(苏教版2019必修第二册)(已下线)专题01 平面向量压轴题(1)-【常考压轴题】(已下线)第一次月考卷03-《重难点题型·高分突破》(人教A版2019必修第二册)山东省烟台市莱州市第一中学2023-2024学年高一第三次质量检测(3月)数学试题福建省浦城第一中学2023-2024学年高一下学期4月期中考试数学试题
名校
3 . 已知集合 为非空数集,定义:
为非空数集,定义:
 ,
,
(1)若集合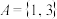 ,直接写出集合
,直接写出集合 ,
, .
.
(2)若集合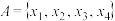 ,
, ,且
,且 ,求证:
,求证:
(3)若集合 ,
, ,
,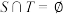 ,记
,记 为集合
为集合 中元素的个数,求
中元素的个数,求 的最大值.
的最大值.
 为非空数集,定义:
为非空数集,定义: ,
,
(1)若集合
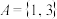 ,直接写出集合
,直接写出集合 ,
, .
.(2)若集合
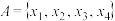 ,
, ,且
,且 ,求证:
,求证:
(3)若集合
 ,
, ,
,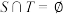 ,记
,记 为集合
为集合 中元素的个数,求
中元素的个数,求 的最大值.
的最大值.
您最近一年使用:0次
2020-11-15更新
|
2791次组卷
|
24卷引用:北京大学附属中学2020-2021学年度高一10月考衔接班数学A层试题
北京大学附属中学2020-2021学年度高一10月考衔接班数学A层试题北京市海淀区中国人民大学附属中学2020-2021学年高一(上)期中数学试题北京市中国人民大学附属中学2020-2021学年度高一年级上学期数学期中练习试题北京人大附中2020-2021学年高一(上)期中数学试题湖南省长沙市湖南师大附中2020-2021学年高一上学期第一次大练习数学试题(已下线)期末测试(能力提升)(1)-2020-2021学年高一数学(必修一)单元测试定心卷(沪教版2020)(已下线)高一上学期期末全真模拟02-2020-2021学年高一数学期末考试高分直通车(沪教版2020,必修一)北京市广渠门中学2021-2022学年高一上学期期中质量检测数学试题北京市延庆区2023-2024学年高二上学期期中考试数学试题(已下线)知识点03 交集、并集-2021-2022学年高一数学同步精品课堂讲+例+测(苏教版2019必修第一册)(已下线)第3课时 课后 集合的基本运算(已下线)第一单元 (基础过关)集合与常用逻辑用语 A卷-【双基双测】2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册)(已下线)第03讲 交集、并集(教师版)-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第一册)第1章 集合(章末测试提高卷)-2021-2022学年高一数学同步单元测试定心卷(苏教版2019必修第一册)(已下线)专题03 集合的运算压轴题型-2021-2022学年高一《新题速递·数学》(人教A版2019)(已下线)1.3 交集、并集(已下线)专题01 集合与逻辑(讲义)-2第一章 预备知识 期末综合复习测评卷-2021-2022学年高一上学期数学北师大版(2019)必修第一册(已下线)第3课时 课后 交集、并集(完成)(已下线)高一上学期期中【易错60题考点专练】(必修一前三章)(已下线)第1章 集合与常用逻辑用语-【优化数学】单元测试基础卷(人教B版2019)(已下线)集合及其运算(已下线)压轴题01 集合与逻辑八种题型-【常考压轴题】(沪教版2020必修第一册)(已下线)高一上学期第一次月考13大压轴考法60题(第1~2章:集合与逻辑+等式与不等式)-【常考压轴题】(沪教版2020必修第一册)
4 . 已知集合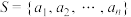 中的元素都是正整数,对任意
中的元素都是正整数,对任意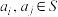 ,定义
,定义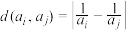 .若存在正整数k,使得对任意
.若存在正整数k,使得对任意 ,都有
,都有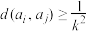 ,则称集合S具有性质
,则称集合S具有性质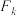 .记
.记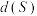 是集合中的
是集合中的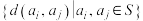 最大值.
最大值.
(1)判断集合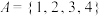 和集合
和集合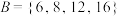 是否具有性质
是否具有性质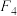 ,直接写出结论;
,直接写出结论;
(2)若集合S具有性质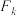 ,求证:
,求证:
①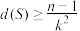 ;
;
②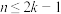 .
.
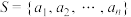 中的元素都是正整数,对任意
中的元素都是正整数,对任意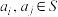 ,定义
,定义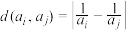 .若存在正整数k,使得对任意
.若存在正整数k,使得对任意 ,都有
,都有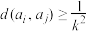 ,则称集合S具有性质
,则称集合S具有性质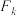 .记
.记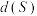 是集合中的
是集合中的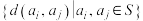 最大值.
最大值.(1)判断集合
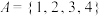 和集合
和集合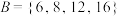 是否具有性质
是否具有性质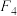 ,直接写出结论;
,直接写出结论;(2)若集合S具有性质
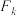 ,求证:
,求证:①
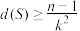 ;
;②
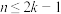 .
.
您最近一年使用:0次
解题方法
5 . 已知椭圆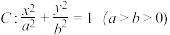 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且 的面积为1.
的面积为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线 与
与 轴交于点C,直线
轴交于点C,直线 与
与 轴交于点D,求证:四边形
轴交于点D,求证:四边形 的面积为定值.
的面积为定值.
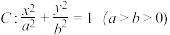 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且 的面积为1.
的面积为1.(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线
 与
与 轴交于点C,直线
轴交于点C,直线 与
与 轴交于点D,求证:四边形
轴交于点D,求证:四边形 的面积为定值.
的面积为定值.
您最近一年使用:0次
2020-03-16更新
|
259次组卷
|
2卷引用:2020届湖北省宜昌市第二中学高三上学期10月月考数学(文)试题
6 . 如图所示,菱形ABCD与正三角形BCE的边长均为2,它们所在的平面互相垂直,DF⊥平面ABCD且DF .
.
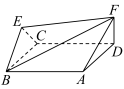
(1)求证:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
 .
.
(1)求证:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
您最近一年使用:0次
2020-03-26更新
|
743次组卷
|
5卷引用:北京市首都师范大学附属中学2020-2021学年高二上学期第一次月考数学试题
名校
7 . 已知集合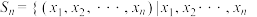 是正整数
是正整数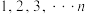 的一个排列
的一个排列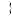
 ,函数
,函数 对于
对于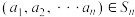 ,定义:
,定义: ,
,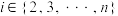 ,
, ,称
,称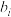 为
为 的满意指数.排列
的满意指数.排列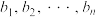 为排列
为排列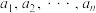 的生成列.
的生成列.
(Ⅰ)当 时,写出排列3,5,1,4,6,2的生成列;
时,写出排列3,5,1,4,6,2的生成列;
(Ⅱ)证明:若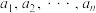 和
和 为
为 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于 中的排列
中的排列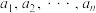 ,进行如下操作:将排列
,进行如下操作:将排列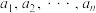 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.
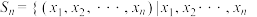 是正整数
是正整数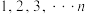 的一个排列
的一个排列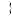
 ,函数
,函数 对于
对于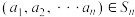 ,定义:
,定义: ,
,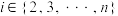 ,
, ,称
,称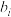 为
为 的满意指数.排列
的满意指数.排列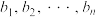 为排列
为排列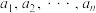 的生成列.
的生成列.(Ⅰ)当
 时,写出排列3,5,1,4,6,2的生成列;
时,写出排列3,5,1,4,6,2的生成列;(Ⅱ)证明:若
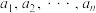 和
和 为
为 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;(Ⅲ)对于
 中的排列
中的排列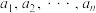 ,进行如下操作:将排列
,进行如下操作:将排列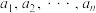 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.
您最近一年使用:0次
2020-12-13更新
|
474次组卷
|
4卷引用:北京市第四中学2021届高三12月数学考试试题
北京市第四中学2021届高三12月数学考试试题北京市第一七一中学2022届高三10月月考数学试题(已下线)北京市第四中学2022届高三10月月考数学试题北京市第八十中学2021-2022学年高一下学期数学线上期末模拟综合练习试题
名校
解题方法
8 . 已知椭圆E: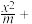 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为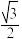 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
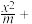 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为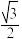 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
您最近一年使用:0次
名校
9 . 对于数列 ,
, ,…,
,…,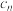 ,记
,记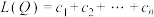 ,
,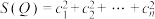 .设数列
.设数列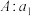 ,
, ,…,
,…, 和数列
和数列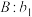 ,
, ,…,
,…, 是两个递增数列,若
是两个递增数列,若 与
与 满足
满足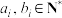 ,
, ,且
,且 ,
, ,则称
,则称 ,
, 具有
具有 关系.
关系.
(Ⅰ)若数列 :4,7,13和数列
:4,7,13和数列 :3,
:3, ,
, 具有
具有 关系,求
关系,求 ,
, 的值;
的值;
(Ⅱ)证明:当 时,存在无数对具有
时,存在无数对具有 关系的数列;
关系的数列;
(Ⅲ)当 时,写出一对具有
时,写出一对具有 关系的数列
关系的数列 和
和 ,并验证你的结论.
,并验证你的结论.
 ,
, ,…,
,…,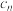 ,记
,记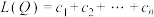 ,
,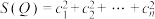 .设数列
.设数列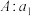 ,
, ,…,
,…, 和数列
和数列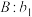 ,
, ,…,
,…, 是两个递增数列,若
是两个递增数列,若 与
与 满足
满足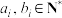 ,
, ,且
,且 ,
, ,则称
,则称 ,
, 具有
具有 关系.
关系.(Ⅰ)若数列
 :4,7,13和数列
:4,7,13和数列 :3,
:3, ,
, 具有
具有 关系,求
关系,求 ,
, 的值;
的值;(Ⅱ)证明:当
 时,存在无数对具有
时,存在无数对具有 关系的数列;
关系的数列;(Ⅲ)当
 时,写出一对具有
时,写出一对具有 关系的数列
关系的数列 和
和 ,并验证你的结论.
,并验证你的结论.
您最近一年使用:0次
10 . 将1至 这
这 个自然数随机填入n×n方格的
个自然数随机填入n×n方格的 个方格中,每个方格恰填一个数(
个方格中,每个方格恰填一个数(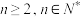 ).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这
).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这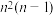 个比值中的最小值,称为这一填数法的“特征值”.
个比值中的最小值,称为这一填数法的“特征值”.
(1)若 ,请写出一种填数法,并计算此填数法的“特征值”;
,请写出一种填数法,并计算此填数法的“特征值”;
(2)当 时,请写出一种填数法,使得此填数法的“特征值”为
时,请写出一种填数法,使得此填数法的“特征值”为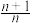 ;
;
(3)求证:对任意一个填数法,其“特征值”不大于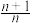 .
.
您最近一年使用:0次
2019-02-14更新
|
259次组卷
|
2卷引用:【区级联考】北京市石景山区2019届高三第一学期期末数学(理)试题



