1 . 已知函数 的定义域为
的定义域为 ,且满足
,且满足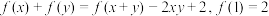 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的定义域为
的定义域为 ,且满足
,且满足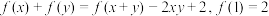 ,则下列结论正确的是( )
,则下列结论正确的是( )A.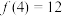 | B.方程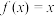 有解 有解 |
C.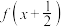 是偶函数 是偶函数 | D.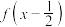 是偶函数 是偶函数 |
您最近一年使用:0次
解题方法
2 . 已知关于 的不等式
的不等式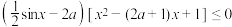 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是______
 的不等式
的不等式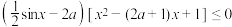 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
解题方法
3 . 函数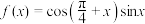 的最小正周期是
的最小正周期是______ .
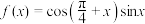 的最小正周期是
的最小正周期是
您最近一年使用:0次
名校
4 . 已知 ,函数
,函数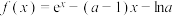 .
.
(1)讨论 的单调性;
的单调性;
(2)若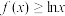 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 ,函数
,函数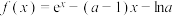 .
.(1)讨论
 的单调性;
的单调性;(2)若
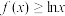 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
1038次组卷
|
5卷引用:福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷
5 . 已知函数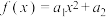 ,
,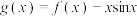 .
.
(1)证明:当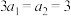 时,曲线
时,曲线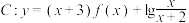 关于点
关于点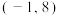 对称;
对称;
(2)若 为曲线
为曲线 的公共点,且
的公共点,且 在
在 处存在共同的切线,则称该切线为
处存在共同的切线,则称该切线为 的“优切线”.若曲线
的“优切线”.若曲线 与曲线
与曲线 存在两条互相垂直的“优切线”,求
存在两条互相垂直的“优切线”,求 ,
, 的值.
的值.
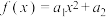 ,
,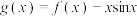 .
.(1)证明:当
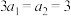 时,曲线
时,曲线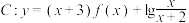 关于点
关于点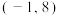 对称;
对称;(2)若
 为曲线
为曲线 的公共点,且
的公共点,且 在
在 处存在共同的切线,则称该切线为
处存在共同的切线,则称该切线为 的“优切线”.若曲线
的“优切线”.若曲线 与曲线
与曲线 存在两条互相垂直的“优切线”,求
存在两条互相垂直的“优切线”,求 ,
, 的值.
的值.
您最近一年使用:0次
2024-09-26更新
|
167次组卷
|
2卷引用:福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷
解题方法
6 . 已知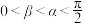 ,
,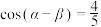 ,
, ,则
,则 ( )
( )
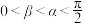 ,
,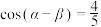 ,
, ,则
,则 ( )
( )A.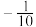 | B.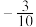 | C. | D. |
您最近一年使用:0次
2024-09-26更新
|
490次组卷
|
3卷引用:福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷
福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷广东省2025届高三上学期9月份联考数学试题(已下线)考点39 两角和与差正切公式的应用 --高考数学100个黄金考点(2025届)【练】
名校
7 . 已知 ,曲线
,曲线 在点
在点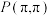 处的切线斜率为
处的切线斜率为 .
.
(1)求 的值;
的值;
(2)求不等式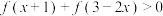 的解集.
的解集.
 ,曲线
,曲线 在点
在点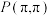 处的切线斜率为
处的切线斜率为 .
.(1)求
 的值;
的值;(2)求不等式
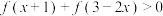 的解集.
的解集.
您最近一年使用:0次
2024-09-19更新
|
1251次组卷
|
4卷引用:福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷
名校
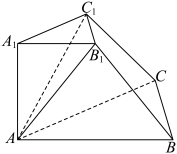
8 . 如图,在三棱台 中,上、下底面是边长分别为4和6的等边三角形,
中,上、下底面是边长分别为4和6的等边三角形, 平面
平面 ,设平面
,设平面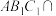 平面
平面 ,点
,点 分别在直线
分别在直线 和直线
和直线 上,且满足
上,且满足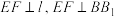 .
.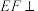 平面
平面 ;
;
(2)若直线 和平面
和平面 所成角的余弦值为
所成角的余弦值为 ,求该三棱台的体积.
,求该三棱台的体积.
 中,上、下底面是边长分别为4和6的等边三角形,
中,上、下底面是边长分别为4和6的等边三角形, 平面
平面 ,设平面
,设平面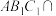 平面
平面 ,点
,点 分别在直线
分别在直线 和直线
和直线 上,且满足
上,且满足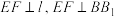 .
.
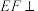 平面
平面 ;
;(2)若直线
 和平面
和平面 所成角的余弦值为
所成角的余弦值为 ,求该三棱台的体积.
,求该三棱台的体积.
您最近一年使用:0次
2024-09-07更新
|
829次组卷
|
3卷引用:福建省龙岩市高级中学2025届高三上学期10月质量监测数学试卷
9 . 如图,在四棱台 中,底面四边形ABCD为菱形,
中,底面四边形ABCD为菱形,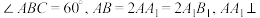 平面ABCD.
平面ABCD.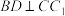 ;
;
(2)若M是棱BC上的点,且满足 ,求二面角
,求二面角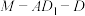 的余弦值.
的余弦值.
 中,底面四边形ABCD为菱形,
中,底面四边形ABCD为菱形,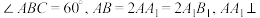 平面ABCD.
平面ABCD.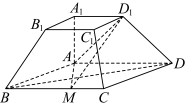
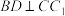 ;
;(2)若M是棱BC上的点,且满足
 ,求二面角
,求二面角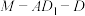 的余弦值.
的余弦值.
您最近一年使用:0次
10 . 已知球的体积为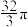 ,且该球的表面积与底面半径为2的圆锥的侧面积相等,则该圆锥的体积为( )
,且该球的表面积与底面半径为2的圆锥的侧面积相等,则该圆锥的体积为( )
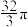 ,且该球的表面积与底面半径为2的圆锥的侧面积相等,则该圆锥的体积为( )
,且该球的表面积与底面半径为2的圆锥的侧面积相等,则该圆锥的体积为( )A.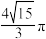 | B.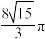 | C.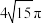 | D.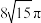 |
您最近一年使用:0次



