1 . 设F为双曲线C: (a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为
(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为
 (a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为
(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为A. | B. |
| C.2 | D. |
您最近一年使用:0次
2019-06-09更新
|
50712次组卷
|
116卷引用:北京市人大附中2020-2021学年度高二年级上学期数学期末练习试题
北京市人大附中2020-2021学年度高二年级上学期数学期末练习试题2019年全国统一高考数学试卷(理科)(新课标Ⅱ)2019年全国统一高考数学试卷(文科)(新课标Ⅱ)(已下线)专题05 平面解析几何——2019年高考真题和模拟题理科数学分项汇编(已下线)专题05 平面解析几何——2019年高考真题和模拟题文科数学分项汇编(已下线)2019年11月20日《每日一题》一轮复习文数-直线与双曲线的位置关系(2)宁夏银川市兴庆区长庆高级中学2019-2020学年高二上学期期中数学(理)试卷(已下线)专题9.6 双曲线(练)-浙江版《 2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题12 圆锥曲线的综合应用-《巅峰冲刺2020年高考之二轮专项提升》(江苏)宁夏育才中学2019-2020学年高二上学期期末考试数学(理)试题2020届天津市红桥区高三下学期高考第一次模拟考试数学试题湖南省衡阳市衡东县欧阳遇实验中学2018-2019学年高二下学期期末数学试题陕西省榆林市绥德中学2019-2020学年高二下学期第一次阶段性测试数学(理)试题安徽省阜阳市太和第一中学2019-2020学年高二(超越班)下学期教学衔接调研考试数学(理)试题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.2综合拔高练(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(文)真题分项(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项(已下线)考点28 双曲线及其性质-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题09 椭圆、双曲线与抛物线的几何性质-2020年高考数学(文)母题题源解密(全国Ⅱ专版)(已下线)专题08 椭圆、双曲线与抛物线的几何性质-2020年高考数学(理)母题题源解密(全国Ⅱ专版)人教A版(2019) 选择性必修第一册 必杀技 第三章 圆锥曲线的方程 第三章素养检测人教B版(2019) 选择性必修第一册 必杀技 第二章 平面解析几何 素养检测人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.6 综合拔高练(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项(已下线)第30练 双曲线-2021年高考数学一轮复习小题必刷(山东专用)(已下线)专题14 圆锥曲线的几何性质-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.4 双曲线(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.6 双曲线(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)专题9.4 双曲线(练)-2021年新高考数学一轮复习讲练测2020学年浙江省嘉兴市高中教师学科专业知识考试数学试题山西省实验中学2020-2021学年高二上学期第三次月考数学(理)试题(已下线)专题9.6 双曲线(精讲)-2021年高考数学(文)一轮复习讲练测(已下线)【新教材精创】2.6.2+双曲线的几何性质(2)+导学案-人教B版高中数学选择性必修第一册(已下线)专题01 数形巧结合,“玩转”离心率(第五篇)-2020高考数学压轴题命题区间探究与突破天津市滨海新区塘沽十三中2020-2021学年高二上学期期中数学试题(已下线)第38练 双曲线-2021年高考数学(文)一轮复习小题必刷(已下线)专题9.4 双曲线 (精讲)-2021年高考数学(文)一轮复习学与练(已下线)专题9.4 双曲线 (精讲)-2021年高考数学(理)一轮复习学与练(已下线)考点36 双曲线的标准方程及几何性质-备战2021年新高考数学一轮复习考点一遍过(已下线)考点37 双曲线-备战2021年高考数学(文)一轮复习考点一遍过 (已下线)解密11 圆锥曲线的方程与性质(分层训练)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(已下线)3.2.2 双曲线的简单几何性质(第1课时)(练习)(已下线)押第7题 双曲线-备战2021年高考数学(理)临考题号押题(全国卷I)(已下线)押第8、11题 圆锥曲线-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)押第15题 双曲线-备战2021年高考数学(文)临考题号押题(全国卷1)(已下线)数学-2021年高考考前20天终极冲刺攻略(二)(新高考地区专用)【学科网名师堂】(5月27日)(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (5月30日)山西省长治市沁源县第一中学2020-2021学年高二下学期开学考试数学(文)试题(已下线)预测10 圆锥曲线中的综合性问题-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】(已下线)解密18 双曲线(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练广东省湛江市2020-2021学年高二下学期期末数学试题江西省宜春市奉新县第一中学2020-2021学年高二下学期第一次月考数学 (文) 试题江西省宜春市丰城市第九中学2020-2021学年高二下学期第三次月考数学(理)试题北师大版(2019) 选修第一册 必杀技 第二章 素养检测新疆乌鲁木齐市第八中学2020-2021学年高二下学期第一阶段考试数学(文)试题苏教版(2019) 选修第一册 必杀技 第三章 素养检测苏教版(2019) 选修第一册 突围者 第3章 章末培优专练北师大版(2019) 选修第一册 突围者 第二章 章末培优专练陕西省榆林市绥德中学2020-2021学年高二下学期6月质量检测文科数学试题(已下线)专题12 解析几何-十年(2012-2021)高考数学真题分项汇编(全国通用)广西南宁市第二中学2018-2019学年高二下学期期末考试数学(文)试题(已下线)考点61 双曲线-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)专题9.4 双曲线 2022年高考数学一轮复习讲练测(新教材新高考)(练)人教B版(2019) 选修第一册 过关检测 第二章 专项把关练(已下线)专题05 平面解析几何(选择题、填空题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)专题15 椭圆、双曲线、抛物线(选择题、填空题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)专题05 双曲线-备战2022年高考数学(文)母题题源解密(全国甲卷)(已下线)考点39 双曲线-备战2022年高考数学典型试题解读与变式河南省南阳市2021-2022学年高三上学期期末数学(文)试题广西百色市2021-2022学年高二上学期期末教学质量调研测试数学(理)试题内蒙古海拉尔第二中学2021-2022学年高三上学期第三次阶段考数学(文)试题河南省南阳市2021-2022学年高三上学期期末数学(文科)试题江苏省南京市第十三中学2021届高三下学期期初数学试题(已下线)易错点17 双曲线-备战2022年高考数学考试易错题(全国通用)(已下线)专题39 盘点圆锥曲线中的离心率问题——备战2022年高考数学二轮复习常考点专题突破(已下线)类型二 椭圆、双曲线、抛物线-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)沪教版(2020) 选修第一册 领航者 第2章 2.3双曲线 第3课时 双曲线的性质(2)(已下线)第30节 双曲线(已下线)专题15 解析几何单选题(已下线)专题18 圆锥曲线选择题(已下线)第61讲 双曲线的标准方程与性质陕西省西安市西北工业大学附属中学2022-2023学年高三上学期第二次适应性训练文科数学试题(已下线)考向33 双曲线(重点)陕西省西安市西北工业大学附属中学2022-2023学年高三上学期第二次适应性训练理科数学试题四川省泸州市龙马高中2022-2023学年高二上学期期中考试数学(文)试题重庆市云阳县高阳中学2022-2023学年高二上学期期末数学试题内蒙古乌兰察布市化德县第一中学2022-2023学年高二上学期期末数学(理)试题(已下线)狂刷48 解析几何的综合问题-学易试题君之小题狂刷2020年高考数学(理)狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)(已下线)专题3.2 双曲线(4类必考点)-2022-2023学年高二数学必考点分类集训系列(人教A版2019选择性必修第一册)内蒙古乌兰察布市化德县第一中学2022-2023学年高二上学期期末考试数学(文)试题陕西省西安市西北工业大学附中2023届高三下学期二模理科数学试题江苏省南京航空航天大学附属高级中学2022-2023学年高二下学期期中数学试题(已下线)模块五 倒数第5天 圆锥曲线(已下线)专题22 圆锥曲线的离心率问题-12.2.2双曲线的简单几何性质(习题)-2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册全国甲乙卷真题5年分类汇编《解析几何》选填四川省泸州市泸县第四中学2022-2023学年高二下学期期末数学文科试题四川省泸州市泸县泸县第四中学2022-2023学年高二下学期期末数学理科试题山西省大同市浑源中学2022-2023学年高二下学期期末数学试题江苏省徐州市邳州市2023-2024学年高二上学期10月阶段性质量检测数学试题湖南省长沙市长郡中学2021-2022学年高二下学期入学考试(寒假作业检测)数学试题四川省成都市第十二中学2023-2024学年高二上学期第三学月月考(12月)数学试题(已下线)3.2.2 双曲线的简单几何性质【第三课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题07 直线与圆(分层练)(已下线)专题16 解析几何选择题(理科)-2(已下线)专题15 解析几何选择题(文科)-2专题22平面解析几何选择填空题(第二部分)专题24平面解析几何选择填空题(第三部分)单元测试B卷——第三章 圆锥曲线的方程【课堂例】2.3.3 双曲线的性质(2) 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线
真题
名校
2 . 已知双曲线C: 的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若
的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若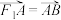 ,
,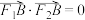 ,则C的离心率为
,则C的离心率为____________ .
 的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若
的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若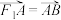 ,
,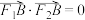 ,则C的离心率为
,则C的离心率为
您最近一年使用:0次
2019-06-09更新
|
42180次组卷
|
100卷引用:北京市海淀区清华大学附属中学2019-2020学年高二上学期期中数学试题
北京市海淀区清华大学附属中学2019-2020学年高二上学期期中数学试题2020届北京市中国人民大学附属中学高三下学期数学统练二试题北京市第八中学2022-2023学年高二上学期期末练习数学试题2019年全国统一高考数学试卷(理科)(新课标Ⅰ)(已下线)专题05 平面解析几何——2019年高考真题和模拟题理科数学分项汇编上海市青浦中学2019-2020学年高三上学期9月月考数学试题(已下线)专题9.6 双曲线(练)-浙江版《 2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(练)【文】-《2020年高考一轮复习讲练测》山东省济宁市兖州区2019-2020学年高二上学期期中数学试题安徽省合肥市第一中学2019-2020学年高二下学期返校考试数学试题广东省化州市第一中学2019-2020学年高二下学期4月线上测试(二)数学试题浙江省嘉兴市第五高级中学2019-2020学年高二上学期期中数学试题(已下线)狂刷46 直线与圆锥曲线的位置关系-学易试题君之小题狂刷2020年高考数学(理)广东省茂名地区2019-2020学年高二上学期期末数学试题上海市曹杨二中2019-2020学年高二下学期期末数学试题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.2综合拔高练(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项(已下线)考点28 双曲线及其性质-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)安徽省合肥一中2019-2020学年高二(下)开学数学试题人教A版(2019) 选择性必修第一册 必杀技 第三章 圆锥曲线的方程 第三章素养检测人教B版(2019) 选择性必修第一册 必杀技 第二章 平面解析几何 素养检测人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.6 综合拔高练(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项江苏省苏州市星海中学2020-2021学年高二上学期期中数学试题(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.4 双曲线(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.6 双曲线(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)专题9.4 双曲线(练)-2021年新高考数学一轮复习讲练测(已下线)考点41 直线与圆锥曲线的位置关系-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.6 双曲线(精讲)-2021年高考数学(文)一轮复习讲练测吉林省长春市第二实验中学2020-2021学年高二上学期期中考试数学(理)试题(已下线)第39练 双曲线-2021年高考数学(理)一轮复习小题必刷(已下线)第2章+章末复习课(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-1)(已下线)第03章+章末复习课(基础练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第一册)(已下线)专题9.4 双曲线 (精讲)-2021年高考数学(文)一轮复习学与练(已下线)专题9.4 双曲线 (精讲)-2021年高考数学(理)一轮复习学与练(已下线)考点36 双曲线的标准方程及几何性质-备战2021年新高考数学一轮复习考点一遍过西藏拉萨中学2021届高三上学期第三次月考数学(文)试题(已下线)专题12 圆锥曲线的方程与性质-备战2021年高考数学(理)二轮复习题型专练?(通用版)(已下线)专题10 圆锥曲线的方程与性质-备战2021年高考数学(文)二轮复习题型专练?(通用版)江苏省苏州大学附属中学2020-2021学年高二下学期3月月考数学试题(已下线)专题3.2 双曲线-2020-2021学年高二数学同步课堂帮帮帮(人教A版2019选择性必修第一册)(已下线)解密11 圆锥曲线的方程与性质(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练安徽省阜阳市颍东区衡水实验中学2020-2021学年高二上学期第四次调研考试数学(理)试题(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (5月30日)(已下线)高二期末押题05-2020-2021学年高二数学下学期期末专项复习(沪教版)(已下线)专题09 圆锥曲线-备战2021年高考数学(理)纠错笔记(已下线)解密19 双曲线(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)预测10 圆锥曲线中的综合性问题-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】北师大版(2019) 选修第一册 必杀技 第二章 素养检测(已下线)卷15 选择性必修第一册高二上期中考试 总复习检测6(难)-2021-2022学年高二数学单元卷模拟(易中难)(2019人教A版选择性必修第一册+第二册)(已下线)考点31 双曲线-备战2022年高考数学(理)一轮复习考点微专题苏教版(2019) 选修第一册 必杀技 第三章 素养检测苏教版(2019) 选修第一册 突围者 第3章 章末培优专练吉林省梅河口市第五中学2021-2022学年高二上学期第一次月考数学试题上海市闵行区七宝中学2019-2020学年高三上学期开学考试数学试题(已下线)专题29 双曲线-2022年高三毕业班数学常考点归纳与变式演练(理科专用)(已下线)专题9.4 双曲线 2022年高考数学一轮复习讲练测(新教材新高考)(练)云南省昆明市第三中学2021-2022学年高二上学期期中考试数学试题辽宁省沈阳市第一二〇中学2021-2022学年高二上学期第四次质量监测数学试题(已下线)专题15 椭圆、双曲线、抛物线(选择题、填空题)-备战2022年高考数学(理)母题题源解密(全国甲卷)黑龙江省双鸭山市第一中学2021-2022学年高三上学期期末考试数学(文)试题(已下线)第三章 圆锥曲线与方程(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)(已下线)易错点17 双曲线-备战2022年高考数学考试易错题(全国通用)陕西省宝鸡市2022届高三下学期二模文科数学试题陕西省宝鸡市2022届高三下学期二模理科数学试题安徽省宣城市2022届高三下学期第二次调研考试文科数学试题(已下线)专题43 盘点圆锥曲线与平面向量交汇问题——备战2022年高考数学二轮复习常考点专题突破沪教版(2020) 选修第一册 新课改一课一练 第4章 阶段复习2(已下线)2022年高考考前20天终极冲刺攻略(三)【理科数学】(5月29日)(已下线)第30节 双曲线(已下线)专题20 圆锥曲线多选、填空题2023版 湘教版(2019) 选修第一册 过关斩将 全书综合测评(已下线)专题19 圆锥曲线与角平分线定理 微点1 圆锥曲线与角平分线定理四川省成都石室中学2022-2023学年高三上学期10月月考数学(理)试题四川省成都石室中学2022-2023学年高三上学期10月月考数学(文)试题江西省上饶市广丰区重点高中2022-2023学年高二上学期期中考试数学试题江苏省南京市第一中学2022-2023学年高二上学期10月阶段检测数学试题(已下线)第02讲 双曲线(讲)(已下线)专题9-3 求椭圆双曲线离心率题型归类-3湖南师范大学附属中学2022-2023学年高二上学期期中数学试题(已下线)专题11 离心率问题速解(精讲精练)-2湖南省株洲世纪星高级中学2022-2023学年高二上学期期末数学试题狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)内蒙古包头市第四中学2022-2023学年高二上学期期末考试数学(理)试题内蒙古赤峰市八校2023届高三第三次统一模拟考试联考理科数学试题全国甲乙卷真题5年分类汇编《解析几何》选填3.2 双曲线江西省南昌市第三中学2024届高三上学期第二次月考(10月)数学试题河南省焦作市博爱县第一中学2023-2024学年高二上学期期中数学试题四川省成都市棠湖外国语学校2023-2024学年高二上学期期末模拟质量检测数学试题河南省南阳市第一中学校2024届高三上学期第六次月考数学试题(已下线)大招29离心率几何化模型(已下线)专题17 解析几何多选、填空(理科)-2(已下线)专题4 求圆锥曲线的离心率(高三压轴小题大全)【讲】专题22平面解析几何选择填空题(第二部分)【课堂练】阶段复习2 随堂练习-沪教版(2020)选择性必修一 第4章 数列(已下线)考点30 平面向量与多学科交汇问题 --高考数学100个黄金考点(2025届)【练】
名校
解题方法
3 . 已知 分别为双曲线
分别为双曲线 的左、右焦点,过
的左、右焦点,过 与双曲线的一条渐近线平行的直线交双曲线于点
与双曲线的一条渐近线平行的直线交双曲线于点 ,若
,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 分别为双曲线
分别为双曲线 的左、右焦点,过
的左、右焦点,过 与双曲线的一条渐近线平行的直线交双曲线于点
与双曲线的一条渐近线平行的直线交双曲线于点 ,若
,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )| A.3 | B. | C. | D.2 |
您最近一年使用:0次
2023-11-23更新
|
5177次组卷
|
16卷引用:黄金卷04
(已下线)黄金卷04四川省成都市成华区某校2023-2024学年高三上学期期中考试数学(理)试题江西省宜春市丰城拖船中学2024届高三上学期期中数学试题江西省宜春市上高县2024届高三上学期12月月考数学试题江西省宜春市铜鼓中学2023届高三上学期第三次阶段性测试数学试题四川省广安第二中学校2023-2024学年高三上学期第二次月考理科数学试题天津市静海区第一中学2024届高三上学期12月月考数学试题福建省福州市永泰县第一中学2023-2024学年高二上学期适应性练习数学试题重庆市沙坪坝区第七中学校2024届高三上学期12月月考数学试题湖南省永州市第一中学2023-2024学年高二上学期第三次月考数学试题福建省三明市第一中学2024届高三上学期月考二(12月)数学试题(已下线)黄金卷04(理科)(已下线)黄金卷02(文科)2024届河北省承德市部分高中二模数学试题河北省衡水市部分学校2024届高三下学期二模考试数学试题专题09双曲线问题(选择填空题)
4 . 若双曲线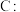
 (
( ,
, )的一条渐近线被圆
)的一条渐近线被圆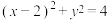 所截
所截
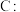
 (
( ,
, )的一条渐近线被圆
)的一条渐近线被圆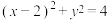 所截
所截得的弦长为2,则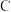 的离心率为
的离心率为
| A.2 | B. | C. | D. |
您最近一年使用:0次
2017-08-07更新
|
32965次组卷
|
103卷引用:北京市东城区2018届高三上学期期中考试数学试题
北京市东城区2018届高三上学期期中考试数学试题(已下线)《高频考点解密》—解密18 圆与方程北京市第十三中学2023届高三上学期12月月考测试数学试题北京大学附属中学2022-2023学年高二下学期期末练习数学试题北京市海淀区中央民族大学附中2024届高三上学期12月月考数学试题2017年全国普通高等学校招生统一考试理科数学(新课标2卷精编版)黑龙江哈尔滨市第三十二中学2018届高三上学期期末考试数学(理)试题2019届高考数学人教A版理科第一轮复习单元测试题:第九章 解析几何人教A版高中数学 高三二轮(文)专题14 椭圆双曲线、抛物线 测试贵州省三都民族中学2017-2018学年高二第二学期第一次月考数学(理)试题(已下线)《高频考点解密》—解密20 双曲线湖北省长阳县第一高级中学2017-2018学年高二下学期期末考试数学(理)试题(已下线)实战演练8.2-2018年高考艺考步步高系列数学浙教版高中数学 高三二轮 专题10 直线与圆锥曲线的基本问题 测试(已下线)2018年12月2日 【理科】人教选修2-1—每周一测(已下线)2018年12月2日 《每日一题》【文科】人教选修1-1—每周一测河北省武邑中学2019届高三上学期期中考试数学(理)试题河北省唐县一中2018-2019学年高二上学期期中考试数学(文)试题山西省晋中市平遥县第二中学2018-2019学年高二12月月考数学(理)试题河北省唐县一中2018-2019学年高二上学期期中考试数学(理)试题【校级联考】吉林省辽源市田家炳高级中学(第六十六届友好学校)2019届高三上学期期末联考数学(理)试题吉林省辽源市田家炳高级中学2019届高三上学期期末考试数学(文)试题【全国百强校】吉林省实验中学2018-2019学年高二上学期期末考试数学(理)试题河北省武邑中学2019届高三上学期期末考试数学(理)试题【市级联考】辽宁省葫芦岛市普通高中2019年高三调研考试数学文科试题【全国百强校】陕西省宝鸡中学2019届高三第一次模拟考试数学(文)试题新疆石河子第二中学2018-2019学年高二下学期期末数学试题智能测评与辅导[理]-双曲线河北省张家口市第一中学2019-2020学年高二上学期期中数学试题宁夏石嘴山市第三中学2019-2020学年高三第四次高考适应性考试数学(理)试题江苏省淮安市淮阴区淮阴中学2019-2020学年高二上学期期末数学试题江苏省淮安市淮阴中学2019-2020学年高二上学期期末考试数学试题(已下线)专题9.4 直线与圆、圆与圆的位置关系(练)【理】-《2020年高考一轮复习讲练测》湖南省郴州市2019-2020学年高二上学期期末数学试题(已下线)专题9.4 直线与圆、圆与圆的位置关系(练)【文】-《2020年高考一轮复习讲练测》安徽省淮北市相山区淮北市第一中学2019-2020学年高二上学期期中数学(理科)试题河北省博野中学2019-2020学年高二上学期12月月考数学试题河北省武邑中学2018-2019学年高三下学期期中数学(理)试题2020届江西省上饶市六校高三一模(4月)文科数学试题陕西省西安市西北大学附中2019-2020学年高二上学期期中数学试题宁夏银川三沙源上游学校2019-2020学年高二上学期期末考试数学(理)试题广东省华美实验学校2019-2020学年高三下学期4月网上考试数学(文)试题江西省上饶市六校2019-2020学年高三下学期第一次联考数学(文)试题(已下线)第十八篇离心率02—2020年高考数学选填题专项测试(文理通用)(已下线)秒杀题型04 离心率(椭圆与双曲线)-2020年高考数学试题调研之秒杀圆锥曲线压轴题河北省石家庄市2019-2020学年高三下学期5月阶段性训练数学(理)试题2020届石家庄市高三年级阶段性训练(理)试题江西省新余市第一中学2019-2020学年高二下学期第一次段考数学(文)试题四川省宜宾市第四中学校2020届高三第一次高考适应性考试数学(理)试题四川省宜宾市第四中学校2020届高三第一次高考适应性考试数学(文)试题江西省宜春实验中学2019-2020学年高二下学期期中考试数学(文)试题(已下线)专题11 双曲线及其性质-2020年高考数学(理)母题题源解密(全国Ⅲ专版)(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项(已下线)考点28 双曲线及其性质-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.6 综合拔高练(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过山东省泰安市宁阳县宁阳一中2020-2021学年高二上学期期中考试数学试题四川省成都市锦江区成都市盐道街中学2020-2021学年高二上学期期中数学试题江苏省无锡市2021届高三下学期2月教学质量检测数学试题山东省聊城市第一中学2021届高三一模检测题(一)数学试题(已下线)数学-2021年高考考前20天终极冲刺攻略(二)(新高考地区专用)【学科网名师堂】(5月27日)(已下线)【新东方】高中数学20210527-007【2021】【高二下】福建省泉州晋江市磁灶中学、内坑中学2021届高三上学期期末联考数学试题湖北省黄冈市黄梅国际育才高级中学2020-2021学年高二下学期3月月考数学试题安徽省安庆市桐城市第八中学2019-2020学年高二下学期期初检测理科数学试题陕西省商洛市洛南中学2020-2021学年高二下学期第二次月考理科数学试题江苏省南京市中华中学2021-2022学年高三上学期暑期学情调研数学试题(已下线)专题12 解析几何-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)专题29 双曲线-2022年高三毕业班数学常考点归纳与变式演练(理科专用)(已下线)专题13圆锥曲线范围最值问题(测)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(测)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)天津市津南区咸水沽第二中学2021-2022学年高二上学期期中数学试题安徽省合肥市第八中学2021-2022学年高二上学期段考(三)文科数学试题内蒙古海拉尔第二中学2021-2022学年高三上学期期末考试数学(文)试题山东省泰安市2022届高三一轮检测(一模)数学试题(已下线)专题39 盘点圆锥曲线中的离心率问题——备战2022年高考数学二轮复习常考点专题突破四川省南充市2022届高考适应性考试(二诊)理科数学试题(已下线)押新高考第11题 圆锥曲线-备战2022年高考数学临考题号押题(新高考专用)江苏省南京、镇江市部分名校2021-2022学年高二下学期5月学情调查考试数学试题青海省西宁市大通县、湟源县2021-2022学年高二下学期期末考试数学(文科)试题 (已下线)专题18 圆锥曲线选择题福建省福州第二中学2021-2022学年高二下学期期末考试数学试题江苏省连云港市灌南高级中学2021-2022学年高二提优班上学期10月月考数学试题(已下线)考向33 双曲线(重点)陕西省西安市高新第一中学2021-2022学年高二上学期期中理科数学试题广东省广州市从化区第三中学2023届高三上学期第三次段考(11月)数学试题陕西省榆林市府谷中学2022-2023学年高二上学期期末线上考试理科数学试题陕西省榆林市府谷中学2022-2023学年高二上学期期末线上考试文科数学试题(已下线)狂刷48 解析几何的综合问题-学易试题君之小题狂刷2020年高考数学(理)狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)吉林省东北师范大学附属中学2022-2023学年高二下学期阶段性验收考试数学试题宁夏银川市唐徕中学2022-2023学年高二下学期3月月考数学(文)试题2.2双曲线的简单几何性质 同步练习-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册海南乐东思源实验高级中学2022-2023学年高二上学期12月月考数学试题内蒙古自治区赤峰市赤峰二中2023-2024学年高二上学期第二次月考数学试题四川省达州市万源中学2023-2024学年高二上学期期中数学试题内蒙古赤峰市赤峰二中2023-2024学年高二上学期第二次月考数学试题安徽省淮北市第一中学2023-2024学年高二上学期第三次月考数学试题天津市和平区第二南开学校2023-2024学年高二上学期第三次月考数学试题四川省凉山州宁南中学2023-2024学年高二上学期期末模拟数学试题(一)(已下线)专题16 解析几何选择题(理科)-2专题22平面解析几何选择填空题(第二部分)
5 . 已知双曲线 :
: 的右顶点为
的右顶点为 ,以
,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,圆
,圆 与双曲线
与双曲线 的一条渐近线于交
的一条渐近线于交 、
、 两点,若
两点,若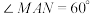 ,则
,则 的离心率为
的离心率为__________ .
 :
: 的右顶点为
的右顶点为 ,以
,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,圆
,圆 与双曲线
与双曲线 的一条渐近线于交
的一条渐近线于交 、
、 两点,若
两点,若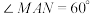 ,则
,则 的离心率为
的离心率为
您最近一年使用:0次
2017-08-07更新
|
27672次组卷
|
68卷引用:《高频考点解密》—解密18 圆与方程
(已下线)《高频考点解密》—解密18 圆与方程北京市首都师范大学附属中学2020-2021学年高二(1-4班)下学期期末数学试题2017年全国普通高等学校招生统一考试理科数学(新课标1卷精编版)广西桂林中学2017-2018学年高二上学期期中考试数学(理)试题天津市河西区新华中学2017-2018学年高二上(文)(理)数学试题安徽省六安市第一中学2017-2018学年高二下学期开学考试数学(理)试题天津市新华中学2017-2018学年高二上学期期中考试数学试题2019届高考数学人教A版理科第一轮复习单元测试题:第九章 解析几何人教A版高中数学 高三二轮(文)专题14 椭圆双曲线、抛物线 测试(已下线)《考前20天终极攻略》5月28日 圆锥曲线【理科】(已下线)《考前20天终极攻略》5月28日 圆锥曲线【理科】【全国百强校】河北省唐山一中2018届高三下学期强化提升考试(一)数学(文)试题(已下线)活页作业19 双曲线的简单性质-2018年数学同步优化指导(北师大版选修2-1)【全国百强校】山东省实验中学(西校区)2019届高三11月模拟考试数学(文)试题(已下线)2019年3月6日 《每日一题》(文)二轮复习-直线与双曲线的位置关系智能测评与辅导[理]-双曲线黑龙江省哈尔滨市第六中学2019-2020学年高二上学期10月份阶段性总结数学(理)试题(已下线)专题9.6 双曲线(讲)-浙江版《2020年高考一轮复习讲练测》湖北省黄冈市浠水县实验高级中学2019-2020学年高三上学期8月月考数学(文)试题(已下线)专题9.6 双曲线(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(讲)【文】-《2020年高考一轮复习讲练测》河北省张家口市第一中学2018-2019学年高一衔接班下学期期末数学试题黑龙江省哈尔滨第六中学2019-2020学年上学期高二10月月考数学理科试题(已下线)秒杀题型04 离心率(椭圆与双曲线)-2020年高考数学试题调研之秒杀圆锥曲线压轴题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.2综合拔高练(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项人教A版(2019) 选择性必修第一册 必杀技 第三章 圆锥曲线的方程 第三章素养检测人教B版(2019) 选择性必修第一册 必杀技 第二章 平面解析几何 素养检测人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.6 综合拔高练湖北省十堰市竹溪一中、竹山一中、房县一中三校2019-2020学年高二下学期7月联考数学试题(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项(已下线)专题10 解析几何小题问题之一角度-备战2020年高考数学二轮痛点突破专项归纳与提高(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.4 双曲线(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.4 双曲线(讲)-2021年新高考数学一轮复习讲练测江西省赣州市第一中学2020-2021学年高二下学期开学测试数学试题(已下线)考点49 直线与双曲线的位置关系(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)专题11 圆锥曲线的几何性质问题 第一篇 热点、难点突破篇(练)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)技巧02 填空题解法与技巧 第二篇 解题技巧篇(练)-2021年高考数学二轮复习讲练测(浙江专用)安徽省池州市第一中学2021届高三下学期高考适应性考试理科数学试题黑龙江省实验中学2021届高三下学期四模数学(文)试题湖南师大附中2019-2020学年高二下学期期末数学试题浙江省宁波市慈溪市2020-2021学年高二下学期期末数学试题北师大版(2019) 选修第一册 必杀技 第二章 素养检测云南省昆明市外国语学校2020-2021学年高二4月月考数学(理)试题苏教版(2019) 选修第一册 必杀技 第三章 素养检测(已下线)专题29 双曲线-2022年高三毕业班数学常考点归纳与变式演练(理科专用)(已下线)专题9.4 双曲线 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)专题13圆锥曲线范围最值问题(测)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(测)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题41 离心率的求值或取值范围问题-学会解题之高三数学万能解题模板【2022版】(已下线)专题39 盘点圆锥曲线中的离心率问题——备战2022年高考数学二轮复习常考点专题突破河北省博野中学2021-2022学年高二上学期12月月考数学试题(已下线)专题20 圆锥曲线多选、填空题沪教版(2020) 25天高考冲刺 双新双基百分百12湖南省长沙市麓山国际实验学校2022-2023学年高二下学期入学考试数学试题(已下线)狂刷48 解析几何的综合问题-学易试题君之小题狂刷2020年高考数学(理)狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)人教B版(2019) 选修第一册 北京名校同步练习册 第二章 平面解析几何初步 2.8直线与圆锥曲线的位置关系(二)广西桂林市桂林中学2020-2021学年高二上学期期中数学(理)试题陕西省咸阳市武功县普集高级中学2023届高三上学期11月期中数学(理)试题(已下线)7.3 双曲线(高考真题素材之十年高考)上海市宝山区2023-2024学年高三下学期二模数学试卷(已下线)专题17 解析几何多选、填空(理科)-2(已下线)大招7 数形结合法扫除代数运算障碍专题22平面解析几何选择填空题(第二部分)【典例题】 2.3.2.1双曲线的性质 课堂例题-沪教版(2020)选择性必修第一册第2章 圆锥曲线贵州省凯里市第三中学2023-2024学年高二上学期期末数学试题
名校
解题方法
6 . 在平面直角坐标系 中,已知双曲线
中,已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, 为双曲线右支上一点,连接
为双曲线右支上一点,连接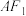 交
交 轴于点
轴于点 .若
.若 为等边三角形,则双曲线
为等边三角形,则双曲线 的离心率为( )
的离心率为( )
 中,已知双曲线
中,已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, 为双曲线右支上一点,连接
为双曲线右支上一点,连接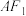 交
交 轴于点
轴于点 .若
.若 为等边三角形,则双曲线
为等边三角形,则双曲线 的离心率为( )
的离心率为( )A. | B. | C. | D.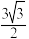 |
您最近一年使用:0次
2023-11-23更新
|
2704次组卷
|
17卷引用:北京市一零一中学2023-2024学年高二上学期期末考试数学试卷
北京市一零一中学2023-2024学年高二上学期期末考试数学试卷北京市第一○一中学2024届高三下学期三模数学试题江苏省南京市2023-2024学年高二上学期期中调研测试数学试题广东省东莞市第十高级中学2023-2024学年高二上学期12月期中考试数学试题湖南省邵阳市邵东市第一中学2023-2024学年高二上学期12月月考数学试题陕西省渭南市2023-2024学高三上学期教学质量检测一(一模)文科数学试题2024届陕西省渭南市高三一模数学(理)试题宁夏吴忠市吴忠中学2023-2024学年高二上学期期末数学试题黑龙江省大庆市大庆实验中学实验二部2023-2024学年高二上学期期末数学试题(已下线)3.2.2 双曲线的几何性质(8大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)广东省深圳市龙岗区华中师大龙岗附属中学2022-2023学年高二上学期期末复习数学测试卷(一)(已下线)专题03 圆锥曲线的方程(4)(已下线)专题19 双曲线离心率定值及取值范围(期末选择题19)-2023-2024学年高二数学上学期期末题型秒杀技巧及专项练习(人教A版2019)(已下线)通关练16 双曲线13考点精练(100题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)江苏省连云港市海头高级中学2023-2024学年高二上学期12月学情检测数学试题【温故练】 第3章 圆锥曲线与方程 章末复习课(一)单元测试-湘教版(2019)选择性必修第一册(已下线)重组7 高二期中真题重组卷(江苏卷)A基础卷
2013·浙江·一模
名校
解题方法
7 . 如图所示, ,
, 是双曲线
是双曲线 :
: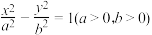 的左、右焦点,过
的左、右焦点,过 的直线与
的直线与 的左、右两支分别交于A,
的左、右两支分别交于A, 两点.若
两点.若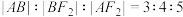 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 ,
, 是双曲线
是双曲线 :
: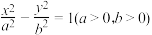 的左、右焦点,过
的左、右焦点,过 的直线与
的直线与 的左、右两支分别交于A,
的左、右两支分别交于A, 两点.若
两点.若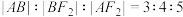 ,则双曲线的离心率为( )
,则双曲线的离心率为( )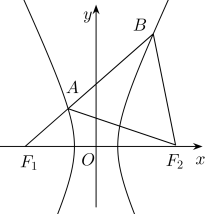
A. |
B. |
C. |
D. |
您最近一年使用:0次
2022-06-20更新
|
4704次组卷
|
38卷引用:北京市人大附中2018届高三第二次模拟考试理科数学试题
北京市人大附中2018届高三第二次模拟考试理科数学试题(已下线)2013届浙江省高三高考模拟测试理科数学试卷(已下线)2013届浙江省临海市白云高级中学高三第三次模拟理科数学试卷(已下线)2014届辽宁省五校协作体届高三摸底考试理科数学试卷(已下线)2014届辽宁省五校协作体届高三摸底考试文科数学试卷(已下线)2014届浙江考试院抽学校高三11月抽测测试理科数学试卷(已下线)2014年高考数学文复习二轮作业手册新课标·通用版限时集18讲练习卷(已下线)2013-2014学年浙江省台州中学高二下学期第一次统练理科数学试卷河南省豫北重点中学2017届高三4月联考数学(文)试题河南省豫北重点中学2017届高三4月联考数学(理)试题陕西省渭南市2018届高三教学质量检测(I)理科数学试题【市级联考】陕西省榆林市2019届高三高考模拟第一次测试数学理科试题(已下线)第十课时 课后 第三章 章末复习山东省烟台莱阳市第一中学2021-2022学年高二下学期开学摸底考试数学试题江苏省盐城市2021-2022学年高二下学期期末模拟数学试题福建省厦门外国语学校2021-2022学年高二下学期数学期末模拟试题(3)江苏省南京市中华中学2022-2023学年高三上学期大练(1)数学试题江苏省扬州中学2022-2023学年高三上学期开学考试数学试题(已下线)专题10 椭圆、双曲线与抛物线(已下线)2.6.2 双曲线的几何性质(1)(已下线)专题16 圆锥曲线焦点弦 微点5 圆锥曲线焦点弦问题综合训练江西省石城县赣源中学2023届高三8月月考数学(文)试题河南省南阳市2022-2023学年高二上学期期中数学试题(已下线)专题12 圆锥曲线压轴小题常见题型全归纳(精讲精练)-2安徽省滁州市定远县育才学校2021-2022学年高二(普通班)上学期期末考试数学(理)试题四川省雅安市2022-2023学年高二上学期期末考试数学(文)试题四川省雅安市2022-2023学年高二上学期期末考试数学(理)试题四川省绵阳市南山中学2022-2023学年高三下学期3月月考数学(理)试题四川省凉山州宁南中学2022-2023学年高二下学期第一次月考理科数学试题人教A版(2019) 选修第一册 第三章 阶段测评(五) 双曲线与抛物线人教A版(2019) 选修第一册 数学奇书 第三章 圆锥曲线的方程 3.3 抛物线 3.3.2 抛物线的简单几何性质 第2课时 抛物线方程及性质的应用湖南省郴州市桂东县第二中学2022-2023学年高二上学期11月月考数学试题四川省仁寿县校际联考2022-2023学年高二下学期第一次质量检测(3月)数学(文)试题宁夏石嘴山市第三中学2016-2017学年高二上学期期末数学(理)试题(已下线)2023-2024学年高二上学期数学期末预测基础卷(人教A版2019)(已下线)特训01 期末选填题汇编(第1-4章,精选60道)-2023-2024学年高二数学《重难点题型·高分突破》(人教A版2019选择性必修第二册)【巩固卷】章末检测试卷(三)单元测试A-湘教版(2019)选择性必修第一册四川省凉山州宁南中学2022-2023学年高二下学期第一次月考数学(文)试题
名校
解题方法
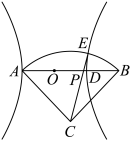
8 . 三等分角是“古希腊三大几何问题”之一,目前尺规作图仍不能解决这个问题.古希腊数学家Pappus(约300~350前后)借助圆弧和双曲线给出了一种三等分角的方法:如图,以角的顶点C为圆心作圆交角的两边于A,B两点;取线段AB的三等分点O,D;以B为焦点,A,D为顶点作双曲线H.双曲线H与弧AB的交点记为E,连接CE,则 .
.________ ;
②若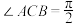 ,
,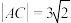 ,CE交AB于点P,则
,CE交AB于点P,则
________ .
 .
.
②若
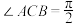 ,
, ,CE交AB于点P,则
,CE交AB于点P,则
您最近一年使用:0次
2023-03-21更新
|
1799次组卷
|
12卷引用:北京市丰台区2023届高三一模数学试题
北京市丰台区2023届高三一模数学试题专题12压轴题汇总(10、15、21题)专题10平面解析几何(非选择题部分)专题03三角函数与解三角形北京市东直门中学2024届高三上学期开学考试数学试题(已下线)北京市丰台区2023届高三下学期3月一模数学试题变式题11-15(已下线)模块六 专题9 易错题目重组卷(安徽卷)(已下线)模块二 情境9 经典数学问题广东省广州市从化区从化中学2023届考前仿真最后模拟数学试题河南省信阳市浉河区信阳高级中学2023届高三三模文数试题广东省汕头市2024届高三上学期期中数学试题江苏省连云港市海州高级中学2024届高三上学期12月阶段测试数学试卷
9 . 在平面直角坐标系 中,若双曲线
中,若双曲线 的右焦点
的右焦点 到一条渐近线的距离为
到一条渐近线的距离为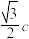 ,则其离心率的值是
,则其离心率的值是________ .
 中,若双曲线
中,若双曲线 的右焦点
的右焦点 到一条渐近线的距离为
到一条渐近线的距离为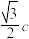 ,则其离心率的值是
,则其离心率的值是
您最近一年使用:0次
2018-06-10更新
|
12146次组卷
|
52卷引用:北京市西城区2019-2020学年高二上学期期末数学试题
北京市西城区2019-2020学年高二上学期期末数学试题北京市第二中学2023-2024学年高二下学期学段考试数学试卷2018年全国普通高等学校招生统一考试数学(江苏卷)(已下线)2018年高考题及模拟题汇编 【文科】6.解析几何(已下线)2018年高考题及模拟题汇编 【理科】6.解析几何【市级联考】甘肃省酒泉地区普通高中五校联考2019届高三上学期月考数学试题(已下线)2018年11月28日 【理科】人教选修2-1—双曲线的离心率及其取值范围(已下线)2018年11月28日 《每日一题》【文科】人教选修1-1—双曲线的离心率及其取值范围(已下线)专题9.6 双曲线(练)-浙江版《 2020年高考一轮复习讲练测》吉林省延边第二中学2019-2020学年高二上学期12月月考数学(文)试题吉林省延边第二中学2019-2020学年高二上学期12月月考数学(理)试题(已下线)专题9.6 双曲线(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题9.6 双曲线(练)-江苏版《2020年高考一轮复习讲练测》河北省宣化第一中学2019-2020学年高二上学期12月月考数学试题(已下线)专题11 圆锥曲线的基本量-《巅峰冲刺2020年高考之二轮专项提升》(江苏)(已下线)秒杀题型05 双曲线的渐近线(双曲线)-2020年高考数学试题调研之秒杀圆锥曲线压轴题(已下线)专题06 双曲线-2020年高考数学母题题源解密(江苏专版)(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(文)真题分项(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项(已下线)考点28 双曲线及其性质-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.2 双曲线 3.2.2 双曲线的简单几何性质(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.6 双曲线(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)专题9.6 双曲线(精练)-2021年高考数学(文)一轮复习讲练测(已下线)第38练 双曲线-2021年高考数学(文)一轮复习小题必刷(已下线)专题11 圆锥曲线的几何性质问题 第一篇 热点、难点突破篇(练)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)考点37 双曲线-备战2021年高考数学(文)一轮复习考点一遍过 (已下线)预测04 平面解析几何-【临门一脚】2020年高考数学三轮冲刺过关(江苏专用)(已下线)3.2.2 双曲线的简单几何性质(1)-2020-2021学年高二数学课时同步练(人教A版选择性必修第一册)(已下线)专题05 平面解析几何-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)课时3.2.2 双曲线(02)双曲线的简单几何性质-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)(已下线)期中考试重难点专题强化训练(3)——圆锥曲线的综合运用-2021-2022学年高二数学单元卷模拟(易中难)(2019人教A版选择性必修第一册+第二册)(已下线)考点61 双曲线-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)卷07 圆锥曲线的方程——章节重难点突破卷-【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)人教B版(2019) 选修第一册 过关检测 第二章 专项把关练海南热带海洋学院附属中学2021届高三10月份月考数学试题湘鄂冀三省益阳平高学校、长沙市平高中学等七校2021-2022学年高二上学期12月联考数学试题天津市滨海新区塘沽第一中学2022-2023学年高二上学期期末数学试题狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)(已下线)安徽省江南十校2022届高三下学期3月一模理科数学试题变式题11-15人教B版(2019) 选修第一册 北京名校同步练习册 第二章 平面解析几何初步 2.8直线与圆锥曲线的位置关系(一)天津市滨海新区田家炳中学2023-2024学年高三上学期期中考试数学试题云南省保山市腾冲市第八中学2022-2023学年高二下学期期中考试数学试卷山东省烟台市爱华高级中学2023-2024学年高二上学期期末模拟数学试题(二)A卷(已下线)专题17 解析几何多选、填空(理科)-2(已下线)专题16 解析几何填空题(文科)-2上海市南洋模范中学2023-2024学年高二下学期5月月考数学试卷湖南省创新高级中学2023-2024学年高二下学期创高杯考试数学试题
真题
名校
10 . 已知椭圆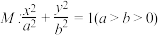 ,双曲线
,双曲线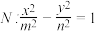 .若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为
.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为__________ ;双曲线N的离心率为__________ .
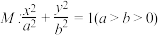 ,双曲线
,双曲线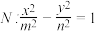 .若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为
.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为
您最近一年使用:0次
2018-06-09更新
|
11454次组卷
|
61卷引用:2018年全国普通高等学校招生统一考试理科数学(北京卷)
2018年全国普通高等学校招生统一考试理科数学(北京卷)北京市朝阳区第八十中学2019-2020学年高二上学期期中数学试题北京一零一中学2022届高三9月开学练习数学试题北京市一零一中学2022届高三下学期入学考试数学试卷题北京市第 八十中学2022-2023学年高二上学期期中考试数学试题(已下线)北京十年真题专题08平面解析几何北京十年真题专题08平面解析几何专题11平面解析几何(第一部分)(已下线)2017-2018学年度下学期高中期末备考 【浙江版】高二【精准复习模拟题】 提高卷02【教师版】(已下线)2018年高考题及模拟题汇编 【理科】6.解析几何(已下线)2018年11月10日——《每日一题》高考一轮复习(理)周末培优(已下线)2019年6月16日 《每日一题》文数-每周一测(已下线)专题9.6 双曲线(练)-浙江版《 2020年高考一轮复习讲练测》山东省日照市2019-2020学年高三下学期1月校际联考数学试题(已下线)专题9.5 椭圆(练)【理】-《2020年高考一轮复习讲练测》(已下线)2020届高三3月第01期(考点08)(文科)-《新题速递·数学》(已下线)2020届高三3月第01期(考点08)(理科)-《新题速递·数学》2020届山东省淄博市部分学校高三下学期3月教学质量检测数学试题(已下线)备战2020年高考数学之考场再现(山东专版)022020届浙江省杭州市高三下学期4月统测模拟数学试题浙江省杭州市萧山中学2017-2018学年学业水平测试数学试题(已下线)狂刷43 椭圆-学易试题君之小题狂刷2020年高考数学(理)(已下线)秒杀题型04 离心率(椭圆与双曲线)-2020年高考数学试题调研之秒杀圆锥曲线压轴题陕西省西安中学2020届高三高考数学(理科)适应性试卷(三)(已下线)2020年秋季高三数学开学摸底考试卷(新高考)04(已下线)第8篇——平面解析几何-新高考山东专题汇编人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.2综合拔高练(已下线)专题07 平面解析几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题05 平面解析几何-五年(2016-2020)高考数学(理)真题分项(已下线)考点28 双曲线及其性质-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)第29练 椭圆-2021年高考数学一轮复习小题必刷(山东专用)(已下线)测试卷21 双曲线-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项(已下线)考点39 双曲线-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.6 双曲线(精练)-2021年高考数学(理)一轮复习讲练测(已下线)专题9.4 双曲线(练)-2021年新高考数学一轮复习讲练测(已下线)2021届高三数学新高考“8+4+4”小题狂练(1)(已下线)专题9.4 双曲线(精练)-2021年新高考数学一轮复习学与练(已下线)痛点15 圆锥曲线中的综合问题-2021年新高考数学一轮复习考点扫描(已下线)第06章+双曲线与抛物线(A卷基础卷)-2020-2021学年高二数学上学期同步单元AB卷(苏教版,新课改地区专用)(已下线)专题18 圆锥曲线中的双曲线与抛物线问题-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】江苏省南通市启东中学2020-2021学年高二上学期第二次月考数学试题(已下线)黄金卷04 【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(广东专用)(已下线)黄金卷13 【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(广东专用)(已下线)专题3.2双曲线(B卷提升篇)-2020-2021学年高二数学选择性必修第一册同步单元AB卷(新教材人教A版,浙江专用)广东省东莞市东华高级中学2021届高三上学期开学摸底数学试题(已下线)考点31 双曲线-备战2022年高考数学(理)一轮复习考点微专题苏教版(2019) 选修第一册 突围者 第3章 章末培优专练(已下线)专题11 圆锥曲线-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)第三章 圆锥曲线的方程 3.2双曲线-2021-2022学年高二数学上学期同步课堂习题测试(人教A版2019选择性必修第一册)人教B版(2019) 选修第一册 过关检测 第二章 第2.6节 综合把关练(已下线)考点39 双曲线-备战2022年高考数学典型试题解读与变式(已下线)专题39 盘点圆锥曲线中的离心率问题——备战2022年高考数学二轮复习常考点专题突破海南华侨中学2021-2022学年高二下学期第一阶段考试数学试题 山东省菏泽市郓城县郓城第一中学2022-2023学年高二上学期期末数学试题(已下线)狂刷48 解析几何的综合问题-学易试题君之小题狂刷2020年高考数学(理)狂刷44+双曲线-学易试题君之小题狂刷2020年高考数学(理)人教B版(2019) 选修第一册 北京名校同步练习册 第二章 平面解析几何初步 2.6双曲线 2.6.2双曲线的几何性质(二)人教A版(2019) 选修第一册 数学奇书 第三章 学业评价(三十)人教A版(2019) 选修第一册 数学奇书 第三章 圆锥曲线的方程 3.2双曲线 3.2.2 双曲线的简单几何性质 第1课时 双曲线的简单几何性质【课后练】3.2.2.1 双曲线的简单几何性质 课后作业-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程



