23-24高三下·广东汕尾·阶段练习
解题方法
1 . 秋空晴澈,微风送爽,绿茵场上,喧腾鼎沸.为吸引同学们积极参与运动,鼓励同学们持之以恒地参与锻炼,养成良好的习惯, 2023年11月我校举办了第十四届田径运动会.来自高三的某学生为了在此次运动会中取得优秀成绩,决定每天在跳远,800m跑和三级蛙跳中选择一个项目训练.第一天在3个项目中任意选一项开始训练,从第二天起,每天都是从前一天没有训练的2个项目中任意选一项训练.
(1)若该学生进行了3天的训练,求第三天训练的是“三级蛙跳”的概率;
(2)设该学生在赛前最后6天训练中选择“跳远”的天数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(1)若该学生进行了3天的训练,求第三天训练的是“三级蛙跳”的概率;
(2)设该学生在赛前最后6天训练中选择“跳远”的天数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
您最近半年使用:0次
2024·湖北武汉·模拟预测
2 . 某校为了丰富课余活动,同时训练学生的逻辑思维能力,在高中三个年级举办中国象棋盲棋比赛,经过各年级初赛,高一、高二、高三分别有3人,4人,5人进入决赛,决赛采取单循环方式,即每名队员与其他队员都要进行1场比赛(每场比赛都采取5局3胜制,初赛、决赛的赛制相同,记分方式相同),最后根据积分选出冠军,积分规则如下:比赛中以3∶0或3∶1取胜的队员积3分,失败的队员积0分;而在比赛中以3∶2取胜的队员积2分,失败的队员积1分.
(1)从进入决赛的12人中随机抽取2人进行表演赛,这2人恰好来自不同年级的概率是多少?
(2)初赛时,高三甲、乙两同学对局,设每局比赛甲取胜的概率均为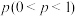 ,记甲以
,记甲以 取胜的概率为
取胜的概率为 ,当
,当 最大时,甲处于最佳竞技状态.在决赛阶段甲、乙对局,而且甲的竞技状态最好,求甲所得积分
最大时,甲处于最佳竞技状态.在决赛阶段甲、乙对局,而且甲的竞技状态最好,求甲所得积分 的分布列及期望.
的分布列及期望.
(1)从进入决赛的12人中随机抽取2人进行表演赛,这2人恰好来自不同年级的概率是多少?
(2)初赛时,高三甲、乙两同学对局,设每局比赛甲取胜的概率均为
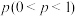 ,记甲以
,记甲以 取胜的概率为
取胜的概率为 ,当
,当 最大时,甲处于最佳竞技状态.在决赛阶段甲、乙对局,而且甲的竞技状态最好,求甲所得积分
最大时,甲处于最佳竞技状态.在决赛阶段甲、乙对局,而且甲的竞技状态最好,求甲所得积分 的分布列及期望.
的分布列及期望.
您最近半年使用:0次
名校
3 . 已知离散型随机变量X 的 分布列如下表:若离散型随机变量 ,则
,则 ( )
( )
 ,则
,则 ( )
( )| X | 0 | 1 | 2 | 3 |
| P | a |  | 5a |  |
A. | B.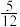 | C.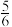 | D. |
您最近半年使用:0次
2024·四川遂宁·二模
4 . 某校在课外活动期间设置了文化艺术类活动和体育锻炼类活动,为了解学生对这两类活动的参与情况,统计了如下数据:
(1)通过计算判断,有没有90%的把握认为该校学生所选择课外活动的类别与性别有关系?
(2)“投壶”是中国古代宴饮时做的一种投掷游戏,也是一种礼仪.该校文化艺术类课外活动中,设置了一项“投壶”活动.已知甲、乙两人参加投壶活动,投中1只得1分,未投中不得分,据以往数据,甲每只投中的概率为 ,乙每只投中的概率为
,乙每只投中的概率为 ,若甲、乙两人各投2只,记两人所得分数之和为
,若甲、乙两人各投2只,记两人所得分数之和为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
其中 ,
, .
.
文化艺术类 | 体育锻炼类 | 合计 | |
男 | 100 | 300 | 400 |
女 | 50 | 100 | 150 |
合计 | 150 | 400 | 550 |
(1)通过计算判断,有没有90%的把握认为该校学生所选择课外活动的类别与性别有关系?
(2)“投壶”是中国古代宴饮时做的一种投掷游戏,也是一种礼仪.该校文化艺术类课外活动中,设置了一项“投壶”活动.已知甲、乙两人参加投壶活动,投中1只得1分,未投中不得分,据以往数据,甲每只投中的概率为
 ,乙每只投中的概率为
,乙每只投中的概率为 ,若甲、乙两人各投2只,记两人所得分数之和为
,若甲、乙两人各投2只,记两人所得分数之和为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 ,
, .
.
您最近半年使用:0次
2024-04-21更新
|
613次组卷
|
4卷引用:8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高
(已下线)8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高四川省遂宁市2024届高三第二次诊断性考试数学(理)试题四川省雅安市2024届高三下学期二诊数学(理)试题四川省乐山市2024届高三第二次调查研究考试数学(理科)试题
23-24高三下·河南·阶段练习
名校
5 . 近日,欧冠拉开帷幕,引得无数球迷的纷纷关注,成了体育竞技赛事的又一热点,为此某中学组织人员对在校学生“是否热爱踢足球”做了一次随机调查.共随机调查了18名男生和12名女生,调查发现,男、女生中分别有12人和6人喜爱该项运动,其余不喜爱.
(1)根据以上数据完成以下 列联表.
列联表.
依据小概率值 的独立性检验,分析性别与喜欢踢足球是否有关?
的独立性检验,分析性别与喜欢踢足球是否有关?
(2)从被调查的女生中随机抽取3人,若其中喜爱踢足球的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中 .
.
(1)根据以上数据完成以下
 列联表.
列联表.| 喜欢踢足球 | 不喜欢踢足球 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
 的独立性检验,分析性别与喜欢踢足球是否有关?
的独立性检验,分析性别与喜欢踢足球是否有关?(2)从被调查的女生中随机抽取3人,若其中喜爱踢足球的人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.附:
 ,其中
,其中 .
. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
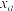 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
名校
解题方法
6 . 袋中有大小相同的小球10个,其中黑球3个,红球 个,白球
个,白球 个,
个, .从中任取2个球,至少有1个红球的概率为
.从中任取2个球,至少有1个红球的概率为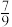 .
.
(1)任取3球,求取出的球中恰有2球同色的概率;
(2)任取2球,取到1个红球得2分,取到1个白球得0分,取到1个黑球得 分,求总得分
分,求总得分 的概率分布列及数学期望
的概率分布列及数学期望 .
.
 个,白球
个,白球 个,
个, .从中任取2个球,至少有1个红球的概率为
.从中任取2个球,至少有1个红球的概率为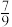 .
.(1)任取3球,求取出的球中恰有2球同色的概率;
(2)任取2球,取到1个红球得2分,取到1个白球得0分,取到1个黑球得
 分,求总得分
分,求总得分 的概率分布列及数学期望
的概率分布列及数学期望 .
.
您最近半年使用:0次
名校
解题方法
7 . 某市举办了党史知识竞赛.初赛采用“两轮制”方式进行,要求每个单位派出两个小组,且每个小组都要参加两轮比赛,两轮比赛都通过的小组才具备参与决赛的资格.某单位派出甲、乙两个小组参赛,在初赛中,若甲小组通过第一轮与第二轮比赛的概率分别是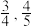 ,乙小组通过第一轮与第二轮比赛的概率分别是
,乙小组通过第一轮与第二轮比赛的概率分别是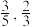 ,且各个小组所有轮次比赛的结果互不影响.
,且各个小组所有轮次比赛的结果互不影响.
(1)若该单位获得决赛资格的小组个数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;
(2)已知甲、乙两个小组都获得了决赛资格,决赛以抢答题形式进行.假设这两组在决赛中对每个问题回答正确的概率恰好是各自获得决赛资格的概率.若最后一道题被该单位的某小组抢到,且甲、乙两个小组抢到该题的可能性分别是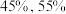 ,该题如果被答对,计算恰好是甲小组答对的概率.
,该题如果被答对,计算恰好是甲小组答对的概率.
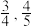 ,乙小组通过第一轮与第二轮比赛的概率分别是
,乙小组通过第一轮与第二轮比赛的概率分别是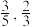 ,且各个小组所有轮次比赛的结果互不影响.
,且各个小组所有轮次比赛的结果互不影响.(1)若该单位获得决赛资格的小组个数为
 ,求
,求 的分布列与数学期望;
的分布列与数学期望;(2)已知甲、乙两个小组都获得了决赛资格,决赛以抢答题形式进行.假设这两组在决赛中对每个问题回答正确的概率恰好是各自获得决赛资格的概率.若最后一道题被该单位的某小组抢到,且甲、乙两个小组抢到该题的可能性分别是
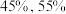 ,该题如果被答对,计算恰好是甲小组答对的概率.
,该题如果被答对,计算恰好是甲小组答对的概率.
您最近半年使用:0次
名校
8 . 为了解居民体育锻炼情况,某地区对辖区内居民体育锻炼进行抽样调查.统计其中400名居民体育锻炼的次数与年龄,得到如下的频数分布表.
(1)若把年龄在 的锻炼者称为青年,年龄在
的锻炼者称为青年,年龄在 的锻炼者称为中年,每周体育锻炼不超过2次的称为体育锻炼频率低,不低于3次的称为体育锻炼频率高,根据数据回答:是否有
的锻炼者称为中年,每周体育锻炼不超过2次的称为体育锻炼频率低,不低于3次的称为体育锻炼频率高,根据数据回答:是否有 的把握认为体育锻炼频率的高低与年龄有关;
的把握认为体育锻炼频率的高低与年龄有关;
(2)从每周体育锻炼5次及以上的样本锻炼者中,按照表中年龄段采用按比例分配的分层随机抽样,抽取8人,再从这8人中随机抽取3人,记这3人中年龄在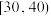 与
与 的人数分别为
的人数分别为 ,求ξ的分布列与期望;
,求ξ的分布列与期望;
(3)已知小明每周的星期六、星期天都进行体育锻炼,且两次锻炼均在跑步、篮球、羽毛球3种运动项目中选择一种,已知小明在某星期六等可能选择一种运动项目,如果星期六选择跑步、篮球、羽毛球,则星期天选择跑步的概率分别为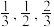 ,求小明星期天选择跑步的概率.
,求小明星期天选择跑步的概率.
参考公式: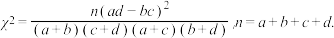
附:
年龄 次数 |  | 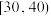 | 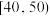 |  |
| 每周0~2次 | 70 | 55 | 36 | 59 |
| 每周3~4次 | 25 | 40 | 44 | 31 |
| 每周5次及以上 | 5 | 5 | 20 | 10 |
 的锻炼者称为青年,年龄在
的锻炼者称为青年,年龄在 的锻炼者称为中年,每周体育锻炼不超过2次的称为体育锻炼频率低,不低于3次的称为体育锻炼频率高,根据数据回答:是否有
的锻炼者称为中年,每周体育锻炼不超过2次的称为体育锻炼频率低,不低于3次的称为体育锻炼频率高,根据数据回答:是否有 的把握认为体育锻炼频率的高低与年龄有关;
的把握认为体育锻炼频率的高低与年龄有关;(2)从每周体育锻炼5次及以上的样本锻炼者中,按照表中年龄段采用按比例分配的分层随机抽样,抽取8人,再从这8人中随机抽取3人,记这3人中年龄在
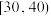 与
与 的人数分别为
的人数分别为 ,求ξ的分布列与期望;
,求ξ的分布列与期望;(3)已知小明每周的星期六、星期天都进行体育锻炼,且两次锻炼均在跑步、篮球、羽毛球3种运动项目中选择一种,已知小明在某星期六等可能选择一种运动项目,如果星期六选择跑步、篮球、羽毛球,则星期天选择跑步的概率分别为
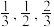 ,求小明星期天选择跑步的概率.
,求小明星期天选择跑步的概率.参考公式:
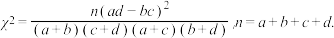
附:
 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
解题方法
9 . 甲,乙两小朋友参加“欢乐六一”游戏比赛,记分规则如下:在一轮比赛中,如果甲赢而乙输,则甲得1分;如果甲输乙赢,则甲得 分;如果甲和乙同时赢或同时输,则甲得0分,设一轮比赛中甲赢的概率为
分;如果甲和乙同时赢或同时输,则甲得0分,设一轮比赛中甲赢的概率为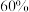 ,乙赢的概率为
,乙赢的概率为 ,求:
,求:
(1)在一轮比赛中,甲的得分 的概率分布列(列表表示);
的概率分布列(列表表示);
(2)在两轮比赛中,甲的得分 的均值与方差.
的均值与方差.
 分;如果甲和乙同时赢或同时输,则甲得0分,设一轮比赛中甲赢的概率为
分;如果甲和乙同时赢或同时输,则甲得0分,设一轮比赛中甲赢的概率为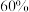 ,乙赢的概率为
,乙赢的概率为 ,求:
,求:(1)在一轮比赛中,甲的得分
 的概率分布列(列表表示);
的概率分布列(列表表示);(2)在两轮比赛中,甲的得分
 的均值与方差.
的均值与方差.
您最近半年使用:0次
名校
解题方法
10 . 据统计,2024年元旦假期,哈尔滨市累计接待游客304.79万人次,实现旅游总收入59.14亿元,游客接待量与旅游总收入达到历史峰值.现对某一时间段冰雪大世界的部分游客做问卷调查,其中 的游客计划只游览冰雪大世界,另外
的游客计划只游览冰雪大世界,另外 的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.
的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.
(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(2)记 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 ;
;
(3)从冰雪大世界的游客中随机抽取100人,这些游客得到纪念品的总个数恰为 个的概率为
个的概率为 ,当
,当 取最大值时,求
取最大值时,求 的值.
的值.
 的游客计划只游览冰雪大世界,另外
的游客计划只游览冰雪大世界,另外 的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.
的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为
 ,求
,求 的分布列及数学期望;
的分布列及数学期望;(2)记
 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 ;
;(3)从冰雪大世界的游客中随机抽取100人,这些游客得到纪念品的总个数恰为
 个的概率为
个的概率为 ,当
,当 取最大值时,求
取最大值时,求 的值.
的值.
您最近半年使用:0次
2024-04-17更新
|
1908次组卷
|
5卷引用:湖南省张家界市慈利县第一中学2023-2024学年高二下学期期中考试数学试卷