1 . 问题解决:(1)如图1,在四边形 中,A为
中,A为 上一点,且
上一点,且 ,若
,若 ,则求证:
,则求证: .
.
拓展探究:(2)如图2,A、B为线段 的垂直平分线上两点,且
的垂直平分线上两点,且 ,过点B作
,过点B作 于E点,
于E点, 的垂直平分线交
的垂直平分线交 于F点,连
于F点,连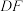 、
、 .试求
.试求 的度数.
的度数.
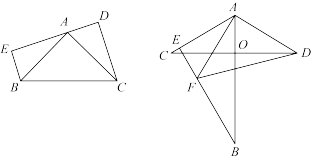
 中,A为
中,A为 上一点,且
上一点,且 ,若
,若 ,则求证:
,则求证: .
.拓展探究:(2)如图2,A、B为线段
 的垂直平分线上两点,且
的垂直平分线上两点,且 ,过点B作
,过点B作 于E点,
于E点, 的垂直平分线交
的垂直平分线交 于F点,连
于F点,连 、
、 .试求
.试求 的度数.
的度数. 
图1 图2
您最近一年使用:0次
名校
2 . 【教材呈现】以下是人教版八年级上册数学教材第53页的部分内容.
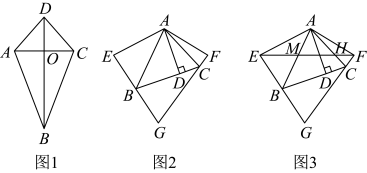
如图1,四边形 中,
中, ,
, .我们把这种两组邻边分别相等的四边形叫做“筝形”.
.我们把这种两组邻边分别相等的四边形叫做“筝形”.
【性质探究】
(1)如图1,连接筝形 的对角线
的对角线 、
、 交于点O,试探究筝形
交于点O,试探究筝形 的性质,并填空:对角线
的性质,并填空:对角线 、
、 的关系是: ;图中
的关系是: ;图中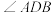 、
、 的大小关系是: .
的大小关系是: .
【概念理解】
(2)如图2,在 中,
中, ,垂足为
,垂足为 ,
,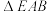 与
与 关于
关于 所在的直线对称,
所在的直线对称,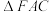 与
与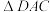 关于
关于 所在的直线对称,延长
所在的直线对称,延长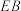 ,
,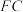 相交于点
相交于点 .请写出图中所有的“筝形”,并选择其中一个进行证明;
.请写出图中所有的“筝形”,并选择其中一个进行证明;
【应用拓展】
(3)如图3,在(2)的条件下,连接 ,分别交
,分别交 、
、 于点
于点 、
、 .求证:
.求证: .
.
如图1,四边形
 中,
中, ,
, .我们把这种两组邻边分别相等的四边形叫做“筝形”.
.我们把这种两组邻边分别相等的四边形叫做“筝形”.
【性质探究】
(1)如图1,连接筝形
 的对角线
的对角线 、
、 交于点O,试探究筝形
交于点O,试探究筝形 的性质,并填空:对角线
的性质,并填空:对角线 、
、 的关系是: ;图中
的关系是: ;图中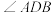 、
、 的大小关系是: .
的大小关系是: .【概念理解】
(2)如图2,在
 中,
中, ,垂足为
,垂足为 ,
,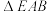 与
与 关于
关于 所在的直线对称,
所在的直线对称,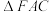 与
与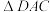 关于
关于 所在的直线对称,延长
所在的直线对称,延长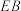 ,
,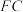 相交于点
相交于点 .请写出图中所有的“筝形”,并选择其中一个进行证明;
.请写出图中所有的“筝形”,并选择其中一个进行证明;【应用拓展】
(3)如图3,在(2)的条件下,连接
 ,分别交
,分别交 、
、 于点
于点 、
、 .求证:
.求证: .
.
您最近一年使用:0次
3 . 【阅读理解】
(1)如图1,在 中,
中, ,
,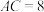 ,D是
,D是 的中点,求
的中点,求 边上的中线
边上的中线 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长 到E,使
到E,使 ,再证明“
,再证明“ ”.探究得出
”.探究得出 的取值范围是
的取值范围是______ ;

【灵活运用】
(2)如图2, 中,
中, ,
, ,
, 是
是 的中线,
的中线, ,
,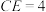 ,且
,且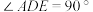 ,求
,求 的长.
的长.

【拓展延伸】
(3)如图3,在 中,
中, 平分
平分 ,且
,且 交
交 于点D,
于点D, 的中点为G,过点G作
的中点为G,过点G作 ,交
,交 于点E,交
于点E,交 的延长线于点F.若
的延长线于点F.若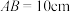 ,
, ,求
,求 .
.

(1)如图1,在
 中,
中, ,
,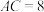 ,D是
,D是 的中点,求
的中点,求 边上的中线
边上的中线 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长 到E,使
到E,使 ,再证明“
,再证明“ ”.探究得出
”.探究得出 的取值范围是
的取值范围是
【灵活运用】
(2)如图2,
 中,
中, ,
, ,
, 是
是 的中线,
的中线, ,
,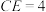 ,且
,且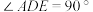 ,求
,求 的长.
的长.
【拓展延伸】
(3)如图3,在
 中,
中, 平分
平分 ,且
,且 交
交 于点D,
于点D, 的中点为G,过点G作
的中点为G,过点G作 ,交
,交 于点E,交
于点E,交 的延长线于点F.若
的延长线于点F.若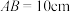 ,
, ,求
,求 .
.
您最近一年使用:0次
名校
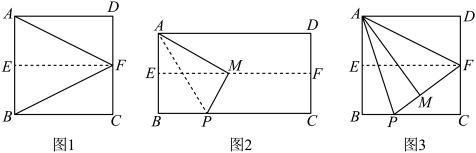
4 . 数学课上,师生们以“利用正方形和矩形纸片折叠特殊角”为主题开展数学活动.
(1)操作判断
小明利用正方形纸片进行折叠,过程如下:
步骤①如图1,对折正方形纸片 ,使
,使 与
与 重合,得到折痕
重合,得到折痕 ,把纸片展平;步骤②:连接
,把纸片展平;步骤②:连接 ,
, ,可以判定
,可以判定 的形状是:______.(直接写出结论)
的形状是:______.(直接写出结论)
(2)探究应用
小华利用矩形纸片进行折叠,过程如下:
如图2,先类似小明的步骤①,得到折痕 后把纸片展平;在
后把纸片展平;在 上选一点
上选一点 ,沿
,沿 折叠
折叠 ,使点
,使点 恰好落在折痕
恰好落在折痕 上的一点
上的一点 处,连接
处,连接 .
.
小华得出的结论是: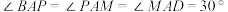 ,请你帮助小华说明理由.
,请你帮助小华说明理由.
(3)拓展迁移
小明受小华的启发,继续利用正方形纸片进行探究,过程如下:
如图3,第一步与步骤(1)一样;然后连接 ,将
,将 沿
沿 折叠,使点
折叠,使点 落在正方形内的一点
落在正方形内的一点 处,连接
处,连接 并延长交
并延长交 于点
于点 ,连接
,连接 ,若正方形的边长是4,请求出
,若正方形的边长是4,请求出 的长.
的长.
(1)操作判断
小明利用正方形纸片进行折叠,过程如下:
步骤①如图1,对折正方形纸片
 ,使
,使 与
与 重合,得到折痕
重合,得到折痕 ,把纸片展平;步骤②:连接
,把纸片展平;步骤②:连接 ,
, ,可以判定
,可以判定 的形状是:______.(直接写出结论)
的形状是:______.(直接写出结论)(2)探究应用
小华利用矩形纸片进行折叠,过程如下:
如图2,先类似小明的步骤①,得到折痕
 后把纸片展平;在
后把纸片展平;在 上选一点
上选一点 ,沿
,沿 折叠
折叠 ,使点
,使点 恰好落在折痕
恰好落在折痕 上的一点
上的一点 处,连接
处,连接 .
.小华得出的结论是:
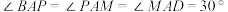 ,请你帮助小华说明理由.
,请你帮助小华说明理由.(3)拓展迁移
小明受小华的启发,继续利用正方形纸片进行探究,过程如下:
如图3,第一步与步骤(1)一样;然后连接
 ,将
,将 沿
沿 折叠,使点
折叠,使点 落在正方形内的一点
落在正方形内的一点 处,连接
处,连接 并延长交
并延长交 于点
于点 ,连接
,连接 ,若正方形的边长是4,请求出
,若正方形的边长是4,请求出 的长.
的长.
您最近一年使用:0次
5 . 综合与实践:
动手操作:某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘.如图1,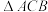 是等腰直角三角形,
是等腰直角三角形,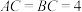 ,
, ,将边
,将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段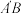 ,连接
,连接 ,过点
,过点 作
作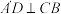 交
交 延长线于点D.
延长线于点D.
思考探索:(1)在图1中: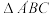 的面积为 ;
的面积为 ;
拓展延伸:(2)如图2,若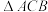 为任意直角三角形,
为任意直角三角形, .将边
.将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段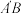 ,连接
,连接 ,过点
,过点 作
作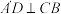 交
交 延长线于点D.猜想三条线段
延长线于点D.猜想三条线段 、
、 、
、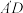 的数量关系,并证明.
的数量关系,并证明.
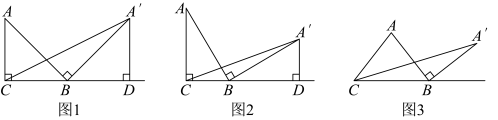
(3)如图3,在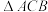 中,
中,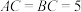 ,
, ,将边
,将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段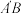 ,连接
,连接 .若点D是
.若点D是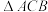 的边
的边 的高线上的一动点,连接
的高线上的一动点,连接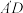 、
、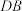 ,则
,则 的最小值是 .
的最小值是 .
动手操作:某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘.如图1,
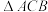 是等腰直角三角形,
是等腰直角三角形,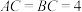 ,
, ,将边
,将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段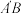 ,连接
,连接 ,过点
,过点 作
作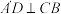 交
交 延长线于点D.
延长线于点D.思考探索:(1)在图1中:
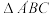 的面积为 ;
的面积为 ;拓展延伸:(2)如图2,若
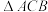 为任意直角三角形,
为任意直角三角形, .将边
.将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段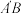 ,连接
,连接 ,过点
,过点 作
作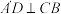 交
交 延长线于点D.猜想三条线段
延长线于点D.猜想三条线段 、
、 、
、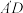 的数量关系,并证明.
的数量关系,并证明.(3)如图3,在
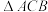 中,
中,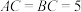 ,
, ,将边
,将边 绕点B顺时针旋转
绕点B顺时针旋转 得到线段
得到线段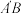 ,连接
,连接 .若点D是
.若点D是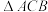 的边
的边 的高线上的一动点,连接
的高线上的一动点,连接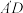 、
、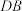 ,则
,则 的最小值是 .
的最小值是 .
您最近一年使用:0次
6 . 探究式学习是新课程提倡的重要学习方式,某兴趣小组拟做以下探究.
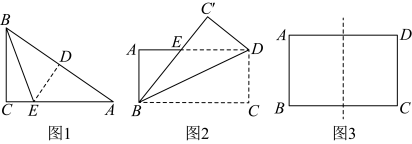
(1)如图1,在三角形纸片 中,
中, ,
,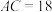 ,将
,将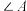 沿
沿 折叠,使点A与点B重合,折痕和
折叠,使点A与点B重合,折痕和 交于点E,
交于点E,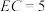 ,求
,求 的长;
的长;
【深入探究】
(2)如图2,将长方形纸片 沿着对角线
沿着对角线 折叠,使点C落在
折叠,使点C落在 处,
处, 交
交 于E,若
于E,若 ,
,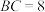 ,求
,求 的长(注:长方形的对边平行且相等);
的长(注:长方形的对边平行且相等);
【拓展延伸】
(3)如图3,在长方形纸片 中,
中, ,
,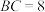 ,点E为射线
,点E为射线 上一个动点,把
上一个动点,把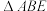 沿直线
沿直线 折叠,当点A的对应点F刚好落在线段
折叠,当点A的对应点F刚好落在线段 的垂直平分线上时,求
的垂直平分线上时,求 的长(注:长方形的对边平行且相等).
的长(注:长方形的对边平行且相等).
(1)如图1,在三角形纸片
 中,
中, ,
,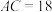 ,将
,将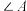 沿
沿 折叠,使点A与点B重合,折痕和
折叠,使点A与点B重合,折痕和 交于点E,
交于点E,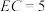 ,求
,求 的长;
的长;【深入探究】
(2)如图2,将长方形纸片
 沿着对角线
沿着对角线 折叠,使点C落在
折叠,使点C落在 处,
处, 交
交 于E,若
于E,若 ,
,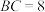 ,求
,求 的长(注:长方形的对边平行且相等);
的长(注:长方形的对边平行且相等);【拓展延伸】
(3)如图3,在长方形纸片
 中,
中, ,
,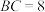 ,点E为射线
,点E为射线 上一个动点,把
上一个动点,把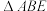 沿直线
沿直线 折叠,当点A的对应点F刚好落在线段
折叠,当点A的对应点F刚好落在线段 的垂直平分线上时,求
的垂直平分线上时,求 的长(注:长方形的对边平行且相等).
的长(注:长方形的对边平行且相等).
您最近一年使用:0次
2024-01-10更新
|
233次组卷
|
3卷引用:辽宁省沈阳市大东区2023-2024学年八年级上学期期末数学试题
辽宁省沈阳市大东区2023-2024学年八年级上学期期末数学试题(已下线)第17章 勾股定理(单元测试·综合卷)-2023-2024学年八年级数学下册基础知识专项突破讲与练(人教版)河南省驻马店市确山县2023-2024学年八年级下学期期中数学试题
名校
7 . 【问题】:如图1,等腰直角三角形 中,
中,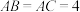 ,
,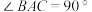 ,
, 是
是 的角平分线,点E为
的角平分线,点E为 上一点,
上一点, 交
交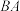 延长线于点F,连接
延长线于点F,连接 ,探究
,探究 ,
, ,
, 之间的数量关系.
之间的数量关系.
【分析】:小明在思考这道题时,先通过测量猜想出 ,然后他想到了老师讲过的“手拉手”模型,便尝试着过点E作
,然后他想到了老师讲过的“手拉手”模型,便尝试着过点E作 的垂线与
的垂线与 相交于点G(如图2),通过证明
相交于点G(如图2),通过证明 ,最终探究出
,最终探究出 ,
, ,
, 之间的数量关系.
之间的数量关系.
(1)请根据小明的思路,补全 的证明过程;
的证明过程;
(2)请直接写出 ,
, ,
, 之间的数量关系;
之间的数量关系;
【应用】(3)当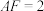 时,请直接写出
时,请直接写出 的长为 ;
的长为 ;
【拓展】(4)若 的中点为点M,当B,E,M三点共线时,请直接写出
的中点为点M,当B,E,M三点共线时,请直接写出 的长为 .
的长为 .

 中,
中,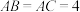 ,
,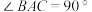 ,
, 是
是 的角平分线,点E为
的角平分线,点E为 上一点,
上一点, 交
交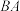 延长线于点F,连接
延长线于点F,连接 ,探究
,探究 ,
, ,
, 之间的数量关系.
之间的数量关系.【分析】:小明在思考这道题时,先通过测量猜想出
 ,然后他想到了老师讲过的“手拉手”模型,便尝试着过点E作
,然后他想到了老师讲过的“手拉手”模型,便尝试着过点E作 的垂线与
的垂线与 相交于点G(如图2),通过证明
相交于点G(如图2),通过证明 ,最终探究出
,最终探究出 ,
, ,
, 之间的数量关系.
之间的数量关系.(1)请根据小明的思路,补全
 的证明过程;
的证明过程;(2)请直接写出
 ,
, ,
, 之间的数量关系;
之间的数量关系;【应用】(3)当
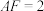 时,请直接写出
时,请直接写出 的长为 ;
的长为 ;【拓展】(4)若
 的中点为点M,当B,E,M三点共线时,请直接写出
的中点为点M,当B,E,M三点共线时,请直接写出 的长为 .
的长为 .
您最近一年使用:0次
8 . 综合与探究
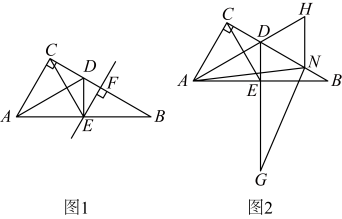
(1)【基础巩固】如图1,在 中,
中, ,
,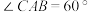 .
. 平分
平分 ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 ,试判断
,试判断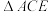 的形状,并说明理由.
的形状,并说明理由.
(2)【深入探究】如图1,在(1)的条件下,连接 ,试猜想
,试猜想 和
和 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)【拓展提高】如图2,在(2)的条件下,N是 上一点,连接
上一点,连接 ,作
,作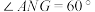 ,交
,交 的延长线于点G,延长
的延长线于点G,延长 到点H,使得
到点H,使得  ,连接
,连接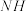 ,试探究
,试探究 和
和 之间的数量关系,并证明你的判断正确.
之间的数量关系,并证明你的判断正确.

(1)【基础巩固】如图1,在
 中,
中, ,
,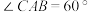 .
. 平分
平分 ,
, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 ,试判断
,试判断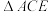 的形状,并说明理由.
的形状,并说明理由.(2)【深入探究】如图1,在(1)的条件下,连接
 ,试猜想
,试猜想 和
和 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(3)【拓展提高】如图2,在(2)的条件下,N是
 上一点,连接
上一点,连接 ,作
,作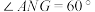 ,交
,交 的延长线于点G,延长
的延长线于点G,延长 到点H,使得
到点H,使得  ,连接
,连接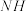 ,试探究
,试探究 和
和 之间的数量关系,并证明你的判断正确.
之间的数量关系,并证明你的判断正确.
您最近一年使用:0次
名校
9 . 当 值相同时,我们把正比例函数
值相同时,我们把正比例函数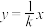 与反比例函数
与反比例函数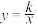 叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以
叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以 与
与 为例对“关联函数”进行了探究.
为例对“关联函数”进行了探究.
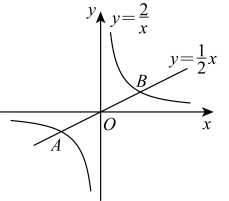
下面是小明的探究过程,请你将它补充完整:
(1)如图,在同一坐标系中画出这两个函数的图象,设这两个函数图象的交点分别为 ,则点
,则点 的坐标为
的坐标为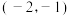 ,点
,点 的坐标为 ;
的坐标为 ;
(2)点 是函数
是函数 在第一象限内的图象上一个动点(点
在第一象限内的图象上一个动点(点 不与点
不与点 重合),设点
重合),设点 的坐
的坐 ,其中
,其中 且
且 .
.
结论1:作直线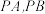 分别与
分别与 轴交于点
轴交于点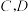 ,则在点
,则在点 运动的过程中,总有
运动的过程中,总有 .
.
证明:①设直线 的解析式为
的解析式为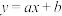 ,将点
,将点 和点
和点 的坐标代入,
的坐标代入,
得 ,解得
,解得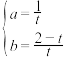 ,
,
则直线 的解析式为
的解析式为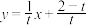 .令
.令 ,可得
,可得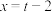 ,
,
则点 的坐标为
的坐标为 .
.
②同理可求,直线 的解析式为
的解析式为 ,点
,点 的坐标为 .
的坐标为 .
③请你继续完成证明 的后续过程;
的后续过程;
④拓展:若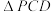 是等边三角形,求点
是等边三角形,求点 的坐标;
的坐标;
⑤结论2:设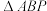 的面积为
的面积为 ,则
,则 是
是 的函数.请你直接写出
的函数.请你直接写出 与
与 的函数表达式.
的函数表达式.
 值相同时,我们把正比例函数
值相同时,我们把正比例函数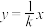 与反比例函数
与反比例函数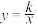 叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以
叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以 与
与 为例对“关联函数”进行了探究.
为例对“关联函数”进行了探究.
下面是小明的探究过程,请你将它补充完整:
(1)如图,在同一坐标系中画出这两个函数的图象,设这两个函数图象的交点分别为
 ,则点
,则点 的坐标为
的坐标为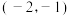 ,点
,点 的坐标为 ;
的坐标为 ;(2)点
 是函数
是函数 在第一象限内的图象上一个动点(点
在第一象限内的图象上一个动点(点 不与点
不与点 重合),设点
重合),设点 的坐
的坐 ,其中
,其中 且
且 .
.结论1:作直线
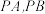 分别与
分别与 轴交于点
轴交于点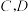 ,则在点
,则在点 运动的过程中,总有
运动的过程中,总有 .
.证明:①设直线
 的解析式为
的解析式为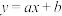 ,将点
,将点 和点
和点 的坐标代入,
的坐标代入,得
 ,解得
,解得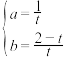 ,
,则直线
 的解析式为
的解析式为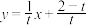 .令
.令 ,可得
,可得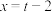 ,
,则点
 的坐标为
的坐标为 .
.②同理可求,直线
 的解析式为
的解析式为 ,点
,点 的坐标为 .
的坐标为 .③请你继续完成证明
 的后续过程;
的后续过程;④拓展:若
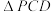 是等边三角形,求点
是等边三角形,求点 的坐标;
的坐标;⑤结论2:设
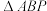 的面积为
的面积为 ,则
,则 是
是 的函数.请你直接写出
的函数.请你直接写出 与
与 的函数表达式.
的函数表达式.
您最近一年使用:0次
10 . 综合与探究

数学兴趣小组活动中,张老师提出了如下问题:如图1,在 中,
中,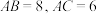 ,求
,求 边上的中线
边上的中线 的取值范围.
的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图2).
①延长 到点
到点 ,使得
,使得 ;
;
②连接 ,通过三角形全等把
,通过三角形全等把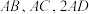 转化在
转化在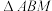 中;
中;
③利用三角形的三边关系可得 的取值范围为
的取值范围为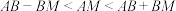 ,从而得到
,从而得到 的取值范围.
的取值范围.
方法总结:上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明各边之间的关系.
(1)根据小明组内的做法,能得到 的依据是_______,
的依据是_______, 边上的中线
边上的中线 的取值范围是_______.
的取值范围是_______.
(2)灵活运用:如图3,在 中,
中, 是
是 的中点,点
的中点,点 在
在 边上,点
边上,点 在
在 边上,若
边上,若 ,求证:
,求证: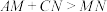 .
.
(3)拓展延伸:以 的边
的边 为边向外作
为边向外作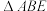 和
和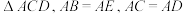 ,
, 是
是 的中点,连接
的中点,连接 .当
.当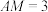 时,请直接写出
时,请直接写出 的长.
的长.

数学兴趣小组活动中,张老师提出了如下问题:如图1,在
 中,
中,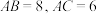 ,求
,求 边上的中线
边上的中线 的取值范围.
的取值范围.小明在组内经过合作交流,得到了如下的解决方法(如图2).
①延长
 到点
到点 ,使得
,使得 ;
;②连接
 ,通过三角形全等把
,通过三角形全等把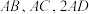 转化在
转化在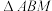 中;
中;③利用三角形的三边关系可得
 的取值范围为
的取值范围为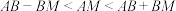 ,从而得到
,从而得到 的取值范围.
的取值范围.方法总结:上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明各边之间的关系.
(1)根据小明组内的做法,能得到
 的依据是_______,
的依据是_______, 边上的中线
边上的中线 的取值范围是_______.
的取值范围是_______.(2)灵活运用:如图3,在
 中,
中, 是
是 的中点,点
的中点,点 在
在 边上,点
边上,点 在
在 边上,若
边上,若 ,求证:
,求证: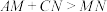 .
.(3)拓展延伸:以
 的边
的边 为边向外作
为边向外作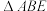 和
和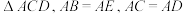 ,
, 是
是 的中点,连接
的中点,连接 .当
.当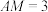 时,请直接写出
时,请直接写出 的长.
的长.
您最近一年使用:0次
2023-11-03更新
|
92次组卷
|
2卷引用:河南省新乡市封丘县城关乡中心学校2022-2023学年八年级上学期期中数学试题



