名校
1 . 关于函数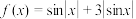 有以下四个结论,其中正确的有( )
有以下四个结论,其中正确的有( )
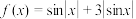 有以下四个结论,其中正确的有( )
有以下四个结论,其中正确的有( )A. 是偶函数 是偶函数 |
B. 的最小值为 的最小值为 |
C.方程 在区间 在区间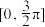 上所有根的和等于 上所有根的和等于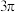 |
D.函数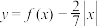 在定义域上有11个零点. 在定义域上有11个零点. |
您最近一年使用:0次
名校
2 . 已知 ,函数
,函数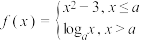 ,下列结论正确的是( )
,下列结论正确的是( )
 ,函数
,函数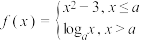 ,下列结论正确的是( )
,下列结论正确的是( )A. |
B.若 在 在 上单调递增,则 上单调递增,则 的取值范围是 的取值范围是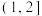 |
C.若函数 有2个零点,则 有2个零点,则 的取值范围是 的取值范围是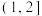 |
D.若 的图象上不存在关于原点对称的点,则 的图象上不存在关于原点对称的点,则 的取值范围是 的取值范围是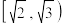 |
您最近一年使用:0次
2024-04-11更新
|
431次组卷
|
3卷引用:湖南省多校联考2023-2024学年高一下学期入学考试数学试题
2024·全国·模拟预测
3 . 已知函数 满足
满足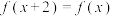 ,且当
,且当 时,
时,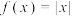 ,有以下四个结论:①
,有以下四个结论:① 的值域是
的值域是 ;②
;② 在
在 上有8个零点;③若方程
上有8个零点;③若方程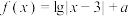 有4个不相等的实数根,则这4个实数根之和为12;④若方程
有4个不相等的实数根,则这4个实数根之和为12;④若方程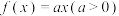 有4个不相等的实数根,则
有4个不相等的实数根,则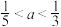 .所有正确结论的序号是
.所有正确结论的序号是______ .
 满足
满足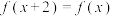 ,且当
,且当 时,
时,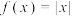 ,有以下四个结论:①
,有以下四个结论:① 的值域是
的值域是 ;②
;② 在
在 上有8个零点;③若方程
上有8个零点;③若方程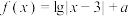 有4个不相等的实数根,则这4个实数根之和为12;④若方程
有4个不相等的实数根,则这4个实数根之和为12;④若方程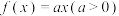 有4个不相等的实数根,则
有4个不相等的实数根,则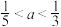 .所有正确结论的序号是
.所有正确结论的序号是
您最近一年使用:0次
名校
4 . 已知定义在 上的奇函数
上的奇函数 ,满足
,满足 ,当
,当 时,
时, ,则下列结论正确的是( )
,则下列结论正确的是( )
 上的奇函数
上的奇函数 ,满足
,满足 ,当
,当 时,
时, ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数 的最小正周期为6 的最小正周期为6 | B.函数 在 在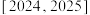 上递增 上递增 |
C.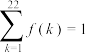 | D.方程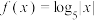 有4个根 有4个根 |
您最近一年使用:0次
2024-04-10更新
|
974次组卷
|
2卷引用:海南省琼海市嘉积中学2023-2024学年高三下学期一模考试数学试题
名校
解题方法
5 . 若关于x的方程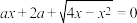 有两个不相等的实数根,则实数a的取值范围是( )
有两个不相等的实数根,则实数a的取值范围是( )
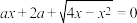 有两个不相等的实数根,则实数a的取值范围是( )
有两个不相等的实数根,则实数a的取值范围是( )A.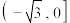 | B.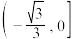 | C.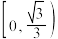 | D. |
您最近一年使用:0次
名校
解题方法
6 . 定义在 上的偶函数
上的偶函数 满足
满足 ,当
,当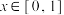 时,
时,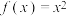 .设函数
.设函数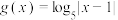 ,则下列结论正确的是( )
,则下列结论正确的是( )
 上的偶函数
上的偶函数 满足
满足 ,当
,当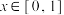 时,
时,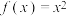 .设函数
.设函数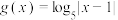 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 的图象关于直线 的图象关于直线 对称 对称 |
B. 的图象在 的图象在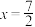 处的切线方程为 处的切线方程为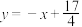 |
C.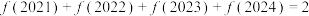 |
D. 的图象与 的图象与 的图象所有交点的横坐标之和为10 的图象所有交点的横坐标之和为10 |
您最近一年使用:0次
名校
解题方法
7 . 函数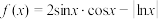 的零点个数为( )
的零点个数为( )
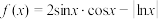 的零点个数为( )
的零点个数为( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
23-24高一下·四川成都·开学考试
名校
解题方法
8 . 已知定义在 上的奇函数
上的奇函数 满足
满足 ,且当
,且当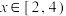 时,
时, ,则下列说法正确的是( )
,则下列说法正确的是( )
 上的奇函数
上的奇函数 满足
满足 ,且当
,且当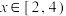 时,
时, ,则下列说法正确的是( )
,则下列说法正确的是( )A.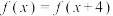 | B. 在 在 上单调递减 上单调递减 |
C.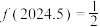 | D.函数 恰有8个零点 恰有8个零点 |
您最近一年使用:0次
名校
9 . 已知函数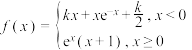 (
( 为自然对数的底数),若关于
为自然对数的底数),若关于 的方程
的方程 有且仅有四个不同的解,则实数
有且仅有四个不同的解,则实数 的取值范围是
的取值范围是________ .
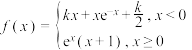 (
( 为自然对数的底数),若关于
为自然对数的底数),若关于 的方程
的方程 有且仅有四个不同的解,则实数
有且仅有四个不同的解,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
2022高一上·全国·专题练习
解题方法
10 . 已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时,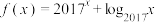 ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次



