1 . 若定义域为 的奇函数
的奇函数 满足
满足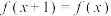 ,则
,则 在
在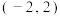 上的零点个数至少为( )
上的零点个数至少为( )
 的奇函数
的奇函数 满足
满足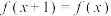 ,则
,则 在
在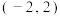 上的零点个数至少为( )
上的零点个数至少为( )| A.5 | B.6 | C.7 | D.8 |
您最近一年使用:0次
解题方法
2 . 已知函数 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意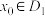 ,恰好存在
,恰好存在 个不同的实数
个不同的实数 ,
,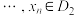 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.
(1)判断 是否为
是否为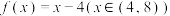 的“
的“ 重覆盖函数”,如果是,求出
重覆盖函数”,如果是,求出 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;
(2)若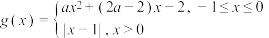 为
为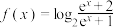 的“3重覆盖函数”,求实数
的“3重覆盖函数”,求实数 的取值范围;
的取值范围;
(3)若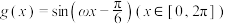 为
为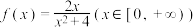 的“2024重覆盖函数”,求正实数
的“2024重覆盖函数”,求正实数 的取值范围.
的取值范围.
 和
和 的定义域分别为
的定义域分别为 和
和 ,若对任意
,若对任意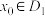 ,恰好存在
,恰好存在 个不同的实数
个不同的实数 ,
,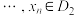 ,使得
,使得 (其中
(其中 ),则称
),则称 为
为 的“
的“ 重覆盖函数”.
重覆盖函数”.(1)判断
 是否为
是否为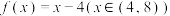 的“
的“ 重覆盖函数”,如果是,求出
重覆盖函数”,如果是,求出 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;(2)若
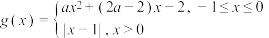 为
为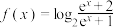 的“3重覆盖函数”,求实数
的“3重覆盖函数”,求实数 的取值范围;
的取值范围;(3)若
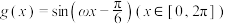 为
为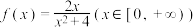 的“2024重覆盖函数”,求正实数
的“2024重覆盖函数”,求正实数 的取值范围.
的取值范围.
您最近一年使用:0次
3 . 下列说法正确的是( )
A.已知方程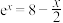 的解在 的解在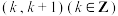 内,则 内,则 |
B.函数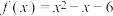 的零点是 的零点是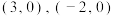 |
C.函数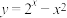 有两个不同的零点 有两个不同的零点 |
D.用二分法求函数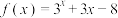 在区间 在区间 内零点近似值的过程中得到 内零点近似值的过程中得到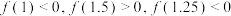 ,则零点近似值在区间 ,则零点近似值在区间 上 上 |
您最近一年使用:0次
解题方法
4 . 设定义在 上的函数
上的函数 满足
满足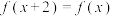 ,
, ,且
,且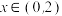 时,
时, ,则方程
,则方程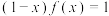 在区间
在区间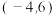 上所有实数根的和为
上所有实数根的和为_____________ .
 上的函数
上的函数 满足
满足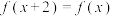 ,
, ,且
,且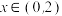 时,
时, ,则方程
,则方程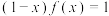 在区间
在区间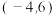 上所有实数根的和为
上所有实数根的和为
您最近一年使用:0次
5 . 已知函数 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )A.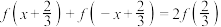 |
B.方程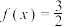 有3个解 有3个解 |
C.当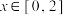 时, 时,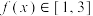 |
D.曲线 有且仅有一条过点 有且仅有一条过点 的切线 的切线 |
您最近一年使用:0次
解题方法
6 . 定义在 上的奇函数
上的奇函数 满足
满足 ,当
,当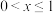 时,
时, ,则函数
,则函数 的零点的个数为
的零点的个数为__________ .
 上的奇函数
上的奇函数 满足
满足 ,当
,当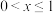 时,
时, ,则函数
,则函数 的零点的个数为
的零点的个数为
您最近一年使用:0次
名校
解题方法
7 . 若函数 满足
满足 且
且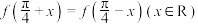 ,则称函数
,则称函数 为“M函数”.
为“M函数”.
(1)试判断 是否为“M函数”,并说明理由;
是否为“M函数”,并说明理由;
(2)函数 为“M函数”,其在
为“M函数”,其在 的图象落在直线
的图象落在直线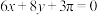 上,在函数
上,在函数 图象上任取一点P,对于定点
图象上任取一点P,对于定点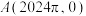 ,求线段AP的最小值;
,求线段AP的最小值;
(3)函数 为“M函数”,且当
为“M函数”,且当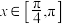 时,
时,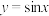 ,求
,求 的解析式;若当
的解析式;若当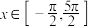 ,关于x的方程
,关于x的方程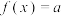 (a为常数)有解,记该方程所有解的和为S,求S.
(a为常数)有解,记该方程所有解的和为S,求S.
 满足
满足 且
且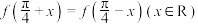 ,则称函数
,则称函数 为“M函数”.
为“M函数”.(1)试判断
 是否为“M函数”,并说明理由;
是否为“M函数”,并说明理由;(2)函数
 为“M函数”,其在
为“M函数”,其在 的图象落在直线
的图象落在直线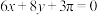 上,在函数
上,在函数 图象上任取一点P,对于定点
图象上任取一点P,对于定点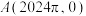 ,求线段AP的最小值;
,求线段AP的最小值;(3)函数
 为“M函数”,且当
为“M函数”,且当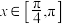 时,
时,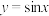 ,求
,求 的解析式;若当
的解析式;若当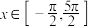 ,关于x的方程
,关于x的方程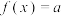 (a为常数)有解,记该方程所有解的和为S,求S.
(a为常数)有解,记该方程所有解的和为S,求S.
您最近一年使用:0次
解题方法
8 . 已知函数 ,其中
,其中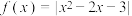 .
. 的零点;
的零点;
(2)讨论关于x的方程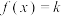 的解的个数;
的解的个数;
(3)若方程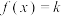 有四个不同的根
有四个不同的根 ,
, ,
, ,
, ,直接写出这四个根的和.
,直接写出这四个根的和.
 ,其中
,其中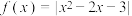 .
.
 的零点;
的零点;(2)讨论关于x的方程
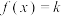 的解的个数;
的解的个数;(3)若方程
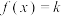 有四个不同的根
有四个不同的根 ,
, ,
, ,
, ,直接写出这四个根的和.
,直接写出这四个根的和.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
9 . 已知函数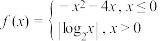 ,若
,若 ,且
,且 ,则下列结论正确的是( )
,则下列结论正确的是( )
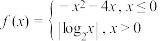 ,若
,若 ,且
,且 ,则下列结论正确的是( )
,则下列结论正确的是( ) A. | B.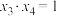 |
C.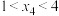 | D.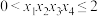 |
您最近一年使用:0次
解题方法
10 . 材料一:我们可以发现这样一个现象:随机生成的一元多项式,在复数集中最终都可以分解成一次因式的乘积,且一次因式的个数(包括重复因式)就是被分解的多项式的次数.事实上,数学中有如下定理:
代数基本定理:任何一元 次复系数多项式方程
次复系数多项式方程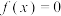 至少有一个复数根.
至少有一个复数根.
材料二:由代数基本定理可以得到:任何一元 次复系数多项式
次复系数多项式 在复数集中可以分解为
在复数集中可以分解为 个一次因式的乘积.进而,一元
个一次因式的乘积.进而,一元 次多项式方程有
次多项式方程有 个复数根(重根按重数计).
个复数根(重根按重数计).
下面我们从代数基本定理出发,看看一元多项式方程的根与系数之间的关系.
设实系数一元二次方程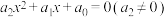
在复数集 内的根为
内的根为 ,容易得到
,容易得到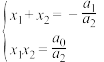
设实系数一一元三次方程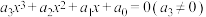 ①
①
在复数集 内的根为
内的根为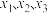 ,可以得到,方程①可变形为
,可以得到,方程①可变形为
展开得: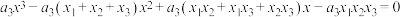 ②
②
比较①②可以得到根与系数之间的关系:
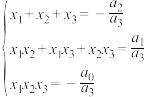
阅读以上材料,利用材料中的方法及学过的知识解决下列问题:
(1)对于方程 在复数集
在复数集 内的根为
内的根为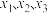 ,求
,求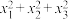 的值;
的值;
(2)如果实系数一元四次方程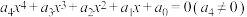 在复数集
在复数集 内的根为
内的根为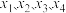 ,试找到根与系数之间的关系;
,试找到根与系数之间的关系;
(3)已知函数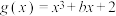 ,对于方程
,对于方程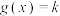 在复数集
在复数集 内的根为
内的根为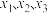 ,当
,当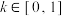 时,求
时,求 的最大值.
的最大值.
代数基本定理:任何一元
 次复系数多项式方程
次复系数多项式方程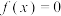 至少有一个复数根.
至少有一个复数根.材料二:由代数基本定理可以得到:任何一元
 次复系数多项式
次复系数多项式 在复数集中可以分解为
在复数集中可以分解为 个一次因式的乘积.进而,一元
个一次因式的乘积.进而,一元 次多项式方程有
次多项式方程有 个复数根(重根按重数计).
个复数根(重根按重数计).下面我们从代数基本定理出发,看看一元多项式方程的根与系数之间的关系.
设实系数一元二次方程
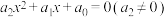
在复数集
 内的根为
内的根为 ,容易得到
,容易得到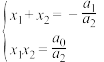
设实系数一一元三次方程
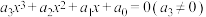 ①
①在复数集
 内的根为
内的根为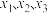 ,可以得到,方程①可变形为
,可以得到,方程①可变形为
展开得:
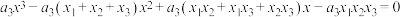 ②
②比较①②可以得到根与系数之间的关系:
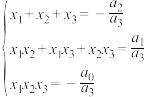
阅读以上材料,利用材料中的方法及学过的知识解决下列问题:
(1)对于方程
 在复数集
在复数集 内的根为
内的根为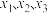 ,求
,求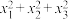 的值;
的值;(2)如果实系数一元四次方程
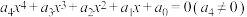 在复数集
在复数集 内的根为
内的根为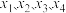 ,试找到根与系数之间的关系;
,试找到根与系数之间的关系;(3)已知函数
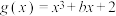 ,对于方程
,对于方程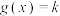 在复数集
在复数集 内的根为
内的根为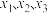 ,当
,当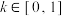 时,求
时,求 的最大值.
的最大值.
您最近一年使用:0次



