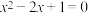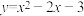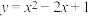2025高三·全国·专题练习
解题方法
1 . 函数 的零点个数为( )
的零点个数为( )
 的零点个数为( )
的零点个数为( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
解题方法
2 . 函数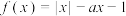 仅有一个零点且该零点为负零点,则
仅有一个零点且该零点为负零点,则 的取值范围是
的取值范围是________ .
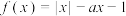 仅有一个零点且该零点为负零点,则
仅有一个零点且该零点为负零点,则 的取值范围是
的取值范围是
您最近一年使用:0次
3 . 填写下面的表格.
方程 |
|
|
|
函数 |
|
|
|
函数的图像 | |||
方程的实数根 | |||
函数的图像与 |
您最近一年使用:0次
4 . 根据函数 在
在 上的图象(如图),确定方程
上的图象(如图),确定方程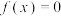 的根的个数.
的根的个数.
 在
在 上的图象(如图),确定方程
上的图象(如图),确定方程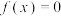 的根的个数.
的根的个数.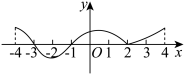
您最近一年使用:0次
解题方法
5 . 已知函数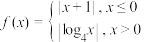 ,若方程
,若方程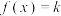 有4个不同的根
有4个不同的根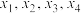 ,且
,且 ,则
,则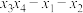 的值为( )
的值为( )
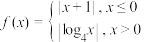 ,若方程
,若方程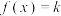 有4个不同的根
有4个不同的根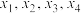 ,且
,且 ,则
,则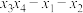 的值为( )
的值为( )| A.3 | B.0 | C.2 | D.6 |
您最近一年使用:0次
6 . 已知函数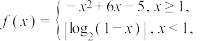 关于
关于 的方程
的方程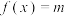 有从小到大排列的四个不同的实数根
有从小到大排列的四个不同的实数根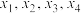 ,若
,若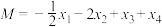 ,则( )
,则( )
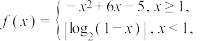 关于
关于 的方程
的方程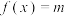 有从小到大排列的四个不同的实数根
有从小到大排列的四个不同的实数根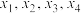 ,若
,若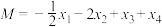 ,则( )
,则( )A.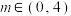 | B. |
C. 的最小值为 的最小值为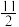 | D. 的最大值为 的最大值为 |
您最近一年使用:0次
解题方法
7 . 设函数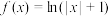 ,
, ,若曲线
,若曲线 与曲线
与曲线 有两个交点,则实数a的取值范围是
有两个交点,则实数a的取值范围是____________ .
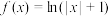 ,
, ,若曲线
,若曲线 与曲线
与曲线 有两个交点,则实数a的取值范围是
有两个交点,则实数a的取值范围是
您最近一年使用:0次
解题方法
8 . 已知正数a,b,c满足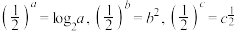 ,则a,b,c大小关系是( )
,则a,b,c大小关系是( )
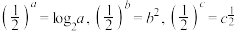 ,则a,b,c大小关系是( )
,则a,b,c大小关系是( )A.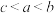 | B.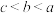 | C. | D.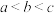 |
您最近一年使用:0次
名校
9 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A. 的图象关于点 的图象关于点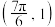 对称 对称 |
B. 的图象关于直线 的图象关于直线 对称 对称 |
C.函数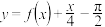 的零点个数为5 的零点个数为5 |
D.函数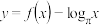 的零点个数为9 的零点个数为9 |
您最近一年使用:0次
解题方法
10 . 已知函数 .
.
(1)当 时,求关于
时,求关于 的方程
的方程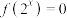 的解;
的解;
(2)若关于 的方程
的方程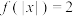 在
在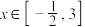 上有两个不相等的解,求
上有两个不相等的解,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求关于
时,求关于 的方程
的方程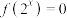 的解;
的解;(2)若关于
 的方程
的方程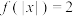 在
在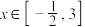 上有两个不相等的解,求
上有两个不相等的解,求 的取值范围.
的取值范围.
您最近一年使用:0次