解题方法
1 . 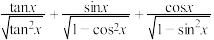 的值可能为( )
的值可能为( )
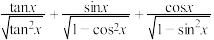 的值可能为( )
的值可能为( )A. | B. | C.1 | D.3 |
您最近一年使用:0次
解题方法
2 . 已知函数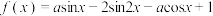 .
.
(1)若 ,求
,求 的最大值及对应的
的最大值及对应的 的取值集合;
的取值集合;
(2)若对任意的 ,
,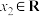 ,
,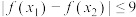 恒成立,求
恒成立,求 的取值范围.
的取值范围.
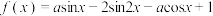 .
.(1)若
 ,求
,求 的最大值及对应的
的最大值及对应的 的取值集合;
的取值集合;(2)若对任意的
 ,
,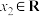 ,
,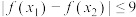 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-24更新
|
127次组卷
|
2卷引用:河南省南阳市2023-2024学年高一下学期5月阶段检测考试数学试题
3 . 已知函数 的定义域为
的定义域为 ,将
,将 的所有零点按照由小到大的顺序排列,记为:
的所有零点按照由小到大的顺序排列,记为: ,……,
,……, ……,对于正整数n有如下两个命题:甲:
……,对于正整数n有如下两个命题:甲: ;乙:
;乙: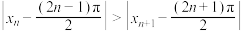 恒成立;则( )
恒成立;则( )
 的定义域为
的定义域为 ,将
,将 的所有零点按照由小到大的顺序排列,记为:
的所有零点按照由小到大的顺序排列,记为: ,……,
,……, ……,对于正整数n有如下两个命题:甲:
……,对于正整数n有如下两个命题:甲: ;乙:
;乙: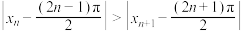 恒成立;则( )
恒成立;则( )| A.甲正确,乙正确 | B.甲正确,乙错误 |
| C.甲错误,乙正确 | D.甲错误,乙错误 |
您最近一年使用:0次
解题方法
4 . 函数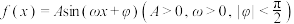 的部分图象如图所示.
的部分图象如图所示. 的解析式;
的解析式;
(2)先将函数 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的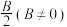 倍,再将图象向左平移
倍,再将图象向左平移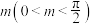 个单位,得到的函数
个单位,得到的函数 为偶函数.若对任意的
为偶函数.若对任意的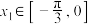 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
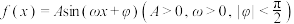 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式;(2)先将函数
 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的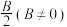 倍,再将图象向左平移
倍,再将图象向左平移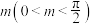 个单位,得到的函数
个单位,得到的函数 为偶函数.若对任意的
为偶函数.若对任意的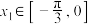 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
5 . 已知函数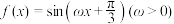 在区间
在区间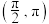 上至少有两个零点,则实数
上至少有两个零点,则实数 的取值范围是( )
的取值范围是( )
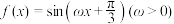 在区间
在区间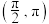 上至少有两个零点,则实数
上至少有两个零点,则实数 的取值范围是( )
的取值范围是( )A.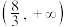 | B.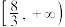 | C. | D.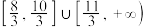 |
您最近一年使用:0次
名校
6 . 已知函数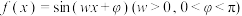 ,相邻两条对称轴的距离为
,相邻两条对称轴的距离为 .
.
(1)若 为偶函数,设
为偶函数,设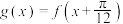 ,求
,求 的单调递增区间;
的单调递增区间;
(2)若 过点
过点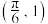 ,设
,设 ,若对任意的
,若对任意的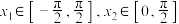 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
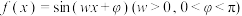 ,相邻两条对称轴的距离为
,相邻两条对称轴的距离为 .
.(1)若
 为偶函数,设
为偶函数,设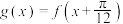 ,求
,求 的单调递增区间;
的单调递增区间;(2)若
 过点
过点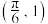 ,设
,设 ,若对任意的
,若对任意的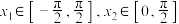 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-06更新
|
596次组卷
|
3卷引用:河南省安阳市林州市第一中学2023-2024学年高一下学期3月检测一数学试题
解题方法
7 . 定义:对于非常数函数 ,若
,若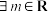 ,
,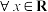 ,
,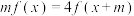 ,则称
,则称 是“米函数”.已知函数
是“米函数”.已知函数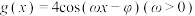 是“米函数”,则ω的最小值为
是“米函数”,则ω的最小值为
您最近一年使用:0次
解题方法
8 . 给定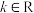 ,若
,若 ,
, 满足
满足 ,均有
,均有 ,则k的范围是( )
,则k的范围是( )
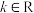 ,若
,若 ,
, 满足
满足 ,均有
,均有 ,则k的范围是( )
,则k的范围是( )A. | B.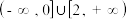 |
C. | D.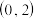 |
您最近一年使用:0次
9 . 下列选项中,正确的有( )
A.函数 的图象关于点 的图象关于点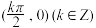 对称. 对称. |
B.函数 是最小正周期为 是最小正周期为 的周期函数. 的周期函数. |
C.设 是第二象限角,则 是第二象限角,则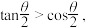 且 且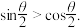 |
D.函数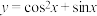 的最小值为 的最小值为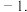 |
您最近一年使用:0次
2024-03-10更新
|
587次组卷
|
3卷引用:陕西省宝鸡市金台区2023-2024学年高一上学期期末质量检测数学试题
陕西省宝鸡市金台区2023-2024学年高一上学期期末质量检测数学试题辽宁省鞍山市第一中学2023-2024学年高一下学期第三次月考数学试卷(已下线)模块四 专题3 重组综合练(陕西)(北师版高一期中)
名校
解题方法
10 . 已知 ,函数
,函数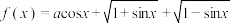 ,其中
,其中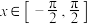 .
.
(1)设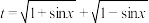 ,求t的取值范围,并把
,求t的取值范围,并把 表示为t的函数
表示为t的函数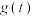 ;
;
(2)求函数 的最大值(可以用a表示);
的最大值(可以用a表示);
 ,函数
,函数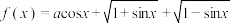 ,其中
,其中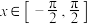 .
.(1)设
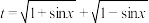 ,求t的取值范围,并把
,求t的取值范围,并把 表示为t的函数
表示为t的函数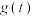 ;
;(2)求函数
 的最大值(可以用a表示);
的最大值(可以用a表示);
您最近一年使用:0次



