名校
1 . 已知函数 ,
, ,
,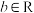 .
.
(1)当 时,判断函数
时,判断函数 的奇偶性并证明;
的奇偶性并证明;
(2)当 且
且 时,利用函数单调性的定义证明函数
时,利用函数单调性的定义证明函数 在
在 上单调递增;
上单调递增;
(3)求证:当 且
且 时,方程
时,方程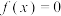 在
在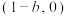 内有实数解.
内有实数解.
 ,
, ,
,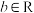 .
.(1)当
 时,判断函数
时,判断函数 的奇偶性并证明;
的奇偶性并证明;(2)当
 且
且 时,利用函数单调性的定义证明函数
时,利用函数单调性的定义证明函数 在
在 上单调递增;
上单调递增;(3)求证:当
 且
且 时,方程
时,方程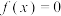 在
在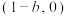 内有实数解.
内有实数解.
您最近一年使用:0次
解题方法
2 . 定义在正实数集上的函数 满足下列条件:
满足下列条件:
①存在常数
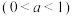 ,使得
,使得 ;②对任意实数
;②对任意实数 ,当
,当 时,恒有
时,恒有 .
.
(1)求证:对于任意正实数 、
、 ,
,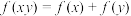 ;
;
(2)证明: 在
在 上是单调减函数;
上是单调减函数;
(3)若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 满足下列条件:
满足下列条件:①存在常数

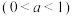 ,使得
,使得 ;②对任意实数
;②对任意实数 ,当
,当 时,恒有
时,恒有 .
.(1)求证:对于任意正实数
 、
、 ,
,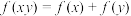 ;
;(2)证明:
 在
在 上是单调减函数;
上是单调减函数;(3)若不等式
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
3 . 已知函数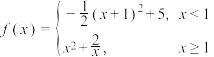 .
.
(1)用单调性定义证明: 在
在 上单调递增;
上单调递增;
(2)若函数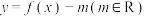 有3个零点
有3个零点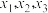 ,满足
,满足 ,且
,且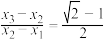 .
.
①求证: ;
;
②求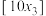 的值(
的值( 表示不超过
表示不超过 的最大整数).
的最大整数).
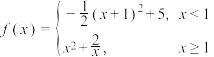 .
.(1)用单调性定义证明:
 在
在 上单调递增;
上单调递增;(2)若函数
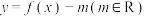 有3个零点
有3个零点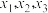 ,满足
,满足 ,且
,且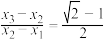 .
.①求证:
 ;
;②求
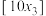 的值(
的值( 表示不超过
表示不超过 的最大整数).
的最大整数).
您最近一年使用:0次
名校
4 . 已知函数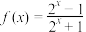 .
.
(1)求证:函数 是定义域为
是定义域为 的奇函数;
的奇函数;
(2)判断函数 的单调性,并用单调性的定义证明.
的单调性,并用单调性的定义证明.
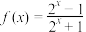 .
.(1)求证:函数
 是定义域为
是定义域为 的奇函数;
的奇函数;(2)判断函数
 的单调性,并用单调性的定义证明.
的单调性,并用单调性的定义证明.
您最近一年使用:0次
2024-01-24更新
|
640次组卷
|
4卷引用:河南省洛阳市强基联盟2023-2024学年高一上学期12月联考数学试题
解题方法
5 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察:(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
阅读材料二:解决多元变量问题时,其中一种思路是运用消元思想将多元问题转化为一元问题,再结合一元问题处理方法进行研究.
例如,正实数 满足
满足 ,求
,求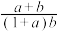 的最小值.
的最小值.
解:由 ,得
,得 ,
,
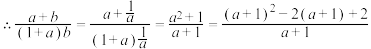
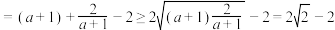 ,
,
当且仅当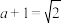 ,即
,即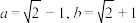 时,等号成立.
时,等号成立.
 的最小值为
的最小值为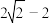 .
.
波利亚在《怎样解题》中指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
结合阅读材料解答下列问题:
(1)已知
 ,求
,求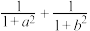 的值;
的值;(2)若正实数
 满足
满足 ,求
,求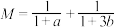 的最小值.
的最小值.
您最近一年使用:0次
6 . 已知函数 ,
,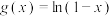 .
.
(1)求证: 为偶函数;
为偶函数;
(2)设 ,判断
,判断 的单调性,并用单调性定义加以证明.
的单调性,并用单调性定义加以证明.
 ,
,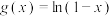 .
.(1)求证:
 为偶函数;
为偶函数;(2)设
 ,判断
,判断 的单调性,并用单调性定义加以证明.
的单调性,并用单调性定义加以证明.
您最近一年使用:0次
解题方法
7 . 在数学中,不给出具体解析式,只给出函数满足的特殊条件或特征的函数称为“抽象函数”.我们需要研究抽象函数的定义域、单调性、奇偶性等性质.对于抽象函数 ,当
,当 时,
时, ,且满足:
,且满足: ,均有
,均有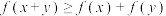
(1)证明: 在
在 上单调递增;
上单调递增;
(2)若函数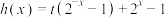 满足上述函数的特征,求实数
满足上述函数的特征,求实数 的取值范围;
的取值范围;
(3)若 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
 ,当
,当 时,
时, ,且满足:
,且满足: ,均有
,均有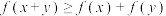
(1)证明:
 在
在 上单调递增;
上单调递增;(2)若函数
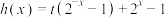 满足上述函数的特征,求实数
满足上述函数的特征,求实数 的取值范围;
的取值范围;(3)若
 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
您最近一年使用:0次
8 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程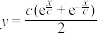 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数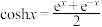 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数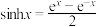 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)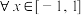 ,不等式
,不等式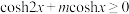 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若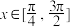 ,试比较
,试比较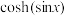 与
与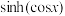 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
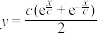 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数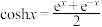 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数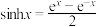 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
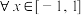 ,不等式
,不等式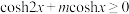 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
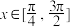 ,试比较
,试比较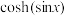 与
与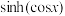 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
885次组卷
|
6卷引用:福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题
福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题
名校
解题方法
9 . 已知函数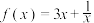 .
.
(1)判断 在
在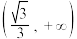 上的单调性,并证明;
上的单调性,并证明;
(2)若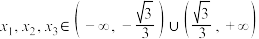 ,且
,且 ,
, ,
, 都为正数,求证:
都为正数,求证: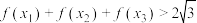 .
.
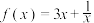 .
.(1)判断
 在
在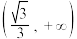 上的单调性,并证明;
上的单调性,并证明;(2)若
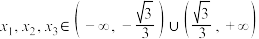 ,且
,且 ,
, ,
, 都为正数,求证:
都为正数,求证: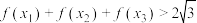 .
.
您最近一年使用:0次
2024-01-26更新
|
190次组卷
|
2卷引用:江苏省泰州市2023-2024学年高一上学期1月期末调研数学试题
名校
解题方法
10 . 已知函数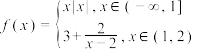
(1)写出 的单调区间以及在每个单调区间上的单调性(无需证明)
的单调区间以及在每个单调区间上的单调性(无需证明)
(2)解不等式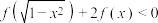
(3)若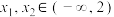 满足
满足 ,且
,且 ,求证:
,求证: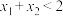
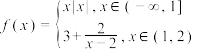
(1)写出
 的单调区间以及在每个单调区间上的单调性(无需证明)
的单调区间以及在每个单调区间上的单调性(无需证明)(2)解不等式
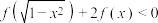
(3)若
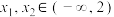 满足
满足 ,且
,且 ,求证:
,求证: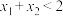
您最近一年使用:0次



